 |
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
|
Repairable Systems Analysis Reference Example |
This example compares the results for a repairable systems analysis.
Reference Case
Crow, L.H., Reliability Analysis for Complex Repairable Systems, Reliability and Biometry: Statistical Analysis of Lifelength, pg. 385, 1974.
Data
The following table shows the data.
| System 1 | System 2 | System 3 |
|---|---|---|
| 4.3 | 0.1 | 8.4 |
| 4.4 | 5.6 | 32.4 |
| 10.2 | 18.6 | 44.7 |
| 23.5 | 19.5 | 48.4 |
| 23.8 | 24.2 | 50.6 |
| 26.4 | 26.7 | 73.6 |
| 74 | 45.1 | 98.7 |
| 77.1 | 45.8 | 112.2 |
| 92.1 | 72.7 | 129.8 |
| 197.2 | 75.7 | 136 |
| 98.6 | 195.8 | |
| 120.1 | ||
| 161.8 | ||
| 180.6 | ||
| 190.8 |
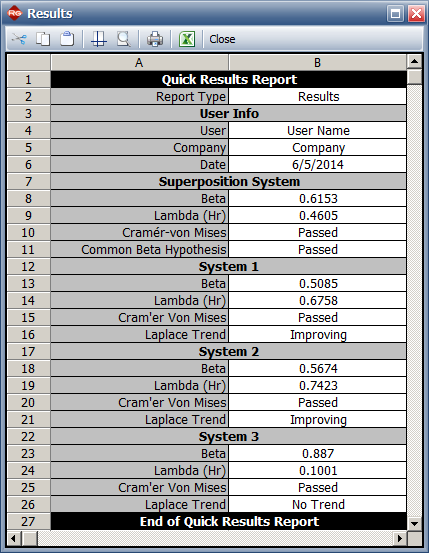
Result
The book has the following results:
Beta = 0.615, Lambda = 0.461
Results in RGA
Since [math]\displaystyle{ \,\!S_{1}=S_{2}=S_{3}=0 }[/math] and [math]\displaystyle{ \,\!T_{1}=T_{2}=T_{3}=200 }[/math] then the maximum likelihood estimates of [math]\displaystyle{ \,\!\hat{\beta} }[/math] and [math]\displaystyle{ \,\!\hat{\lambda } }[/math] are given by:
