Crow Extended

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images, more targeted search and the latest content available as a PDF. As of September 2023, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest reference at help.reliasoft.com/reference/reliability_growth_and_repairable_system_analysis

Chapter 8: Crow Extended

Chapter 8

Crow Extended

Available Software:
RGA

More Resources:
RGA examples

In a previous chapter, we discussed the most widely used traditional reliability growth tracking model, Crow-AMSAA (NHPP). Using this model for reliability growth analysis assumes that the corrective actions for the observed failure modes are incorporated during the test (test-fix-test). However, in actual practice, fixes may be delayed until after the completion of the test (test-find-test) or some fixes may be implemented during the test while others are delayed (test-fix-find-test). At the end of a test phase, two reliability estimates are of concern: demonstrated reliability and projected reliability. The demonstrated reliability, which is based on data generated during the test phase, is an estimate of the system reliability for its configuration at the end of the test phase. The projected reliability measures the impact of the delayed fixes at the end of the current test phase.

Most of the reliability growth literature has been concerned with procedures and models for calculating the demonstrated reliability and very little attention has been paid to techniques for reliability projections. The procedure for making reliability projections utilizes engineering assessments of the effectiveness of the delayed fixes for each observed failure mode. These effectiveness factors are then used with the data generated during the test phase to obtain a projected estimate for the updated configuration by adjusting the number of failures observed during the test phase. The process of estimating the projected reliability is accomplished using the Crow Extended model. The Crow Extended model allows for a flexible growth strategy that can include corrective actions performed during the test, as well as delayed corrective actions. The test-find-test and test-fix-find-test scenarios are simply subsets of the Crow Extended model.

Background

When a system is tested and failure modes are observed, management can make one of two possible decisions, either to fix or not fix the failure mode. Therefore, the management strategy places failure modes into two categories: A modes and B modes. A modes are all failure modes such that when seen during the test no corrective action will be taken. This accounts for all modes for which management determines that it is not economically or otherwise justified to take a corrective action. In order to provide the assessment and management metric structure for corrective actions during and after a test, two types of B modes are defined. BC modes are corrected during the test and the corrective actions for BD modes are delayed until the end of the test. The management strategy is defined by how the corrective actions, if any, will be implemented. In summary, the classifications are defined as follows:

A indicates that no corrective action was performed or will be performed (management chooses not to address for technical, financial or other reasons).

BC indicates that the corrective action was implemented during the test. The analysis assumes that the effect of the corrective action was experienced during the test (as with other test-fix-test reliability growth analyses).

BD indicates that the corrective action will be delayed until after the completion of the current test.

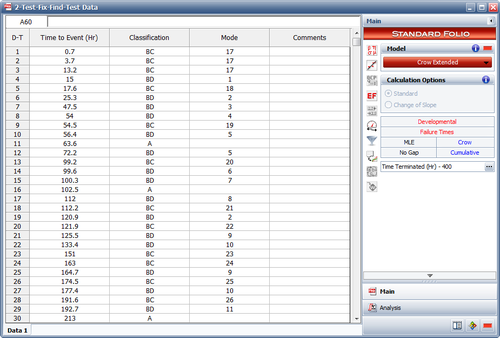
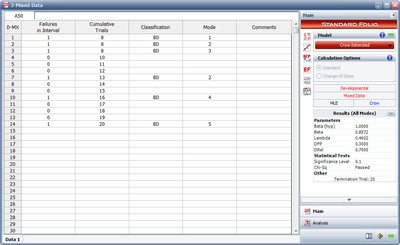
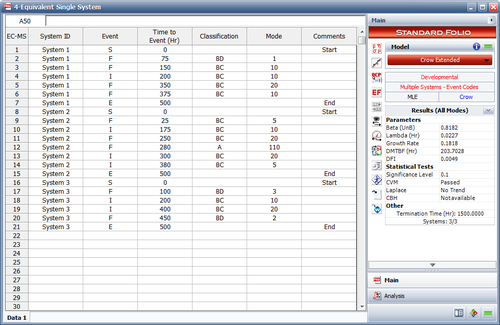
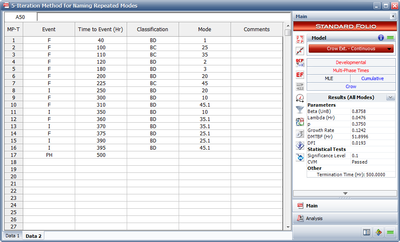
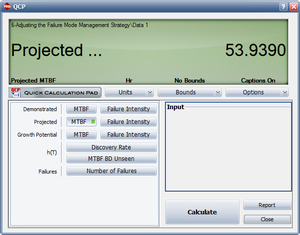
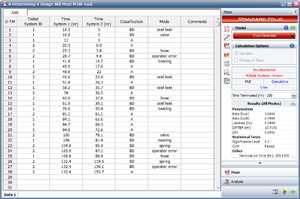
The following picture shows an example of data entered for the Crow Extended model.

Failure times data for a single system in cumulative format, including classification and mode information.

As you can see, each failure is indicated with A, BC or BD in the Classification column. In addition, any number or text can be used to specify the mode. In this example, numbers were used in the Mode column for simplicity, but you could just as easily use Seal Leak, or whatever designation you deem appropriate for identifying the failure mode.

Reliability growth is achieved by decreasing the failure intensity. The failure intensity for the A failure modes will not change. Therefore, reliability growth can only be achieved by decreasing the BC and BD mode failure intensity. It is also clear that, in general, the only part of the BD mode failure intensity that can be decreased is that which has been seen during testing, since the failure intensity due to BD modes that were unseen during testing still remains. BC failure modes are corrected during test and the BC failure intensity will not change any more at the end of test.

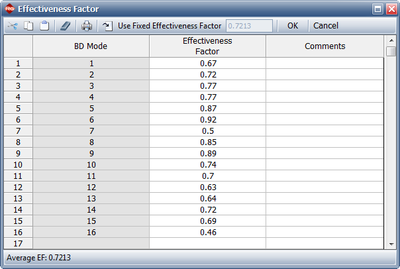
It is very important to note that once a BD failure mode is in the system it is rarely totally eliminated by a corrective action. After a BD mode has been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will generally remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective you will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made and must be a value between 0 and 1. A study on EFs showed that an average EF [math]\displaystyle{ d }[/math] was about 70 percent. Therefore, typically about 30 percent, i.e. 100 [math]\displaystyle{ (1-d) }[/math] percent, of the BD mode failure intensity will remain in the system after all of the corrective actions have been implemented. However, individual EFs for the failure modes may be larger or smaller than the average. The next figure displays the RGA software's Effectiveness Factor window where the effectiveness factors for each unique BD failure mode can be specified.

Effectiveness factors defined for each unique BD mode.

Test-Find-Test

Test-find-test is the case where all corrective actions are delayed until after the test. Therefore, there are no BC modes when analyzing test-find-test data. This scenario is also called the Crow-AMSAA Projection model, but for the purposes of the RGA software it is simply a special case of the Crow Extended model. Suppose a system is subjected to development testing for a period of time, [math]\displaystyle{ T }[/math] . The system can be considered as consisting of two types of failure modes: A modes and BD modes. It is assumed that all BD modes are in series and fail independently according to the exponential distribution. Also assume that the rate of occurrence of A modes follows an exponential distribution with failure intensity [math]\displaystyle{ {{\lambda }_{A}} }[/math] . The system MTBF is constant throughout the test phase since all of the corrective actions are delayed until after the completion of the test. After the delayed fixes have been implemented, the system MTBF will then jump to a higher value.

Let [math]\displaystyle{ K }[/math] denote the total number of BD modes in the system and let [math]\displaystyle{ {{\lambda }_{i}} }[/math] denote the failure intensity for the [math]\displaystyle{ {{i}^{th}} }[/math] BD mode, such that [math]\displaystyle{ i }[/math] = [math]\displaystyle{ 1,2,\ldots ,K }[/math] . Then, at time equal to zero, the system failure intensity [math]\displaystyle{ r(0) }[/math] is:

[math]\displaystyle{ r(0)={{\lambda }_{A}}+{{\lambda }_{BD}} }[/math]

where:

[math]\displaystyle{ {{\lambda }_{BD}}=\underset{i=1}{\overset{K}{\mathop{\sum }}}\,{{\lambda }_{i}} }[/math] .

During the test [math]\displaystyle{ (0,T) }[/math] , a random number of [math]\displaystyle{ M }[/math] distinct BD modes will be observed, such that [math]\displaystyle{ M\le K }[/math] . Denote the effectiveness factor (EF) for the [math]\displaystyle{ {{i}^{th}} }[/math] BD mode as [math]\displaystyle{ {{d}_{i}} }[/math] , [math]\displaystyle{ i }[/math] = [math]\displaystyle{ 1,2,\ldots ,K }[/math] . The effectiveness factor [math]\displaystyle{ {{d}_{i}} }[/math] is the percent decrease in [math]\displaystyle{ {{\lambda }_{i}} }[/math] after a corrective action has been made for the [math]\displaystyle{ {{i}^{th}} }[/math] BD mode. That is, the corrective action for the [math]\displaystyle{ {{i}^{th}} }[/math] BD mode removes [math]\displaystyle{ 100\times {{d}_{i}} }[/math] percent of the failure rate and [math]\displaystyle{ 100\times (1-{{d}_{i}}) }[/math] percent remains. The failure intensity for the [math]\displaystyle{ {{i}^{th}} }[/math] BD failure mode after a corrective action is [math]\displaystyle{ (1-{{d}_{i}}){{\lambda }_{i}} }[/math] . If corrective actions are taken on the [math]\displaystyle{ M }[/math] BD modes observed by time [math]\displaystyle{ T }[/math] , then the system failure intensity is reduced from [math]\displaystyle{ r(0) }[/math] to:

[math]\displaystyle{ \begin{align} & r\left( T \right)= & {{\lambda }_{A}}+\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{i}} \right){{\lambda }_{i}}+({{\lambda }_{BD}}-\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\lambda }_{i}}) \\ & = & {{\lambda }_{A}}+{{\lambda }_{BD}}-\underset{i=1}{\overset{M}{\mathop \sum }}\,{{d}_{i}}{{\lambda }_{i}} \end{align} }[/math]

where:

• [math]\displaystyle{ \underset{i=1}{\overset{M}{\mathop{\sum }}}\,(1-{{d}_{i}}){{\lambda }_{i}} }[/math] is the failure intensity for the [math]\displaystyle{ M }[/math] modes after the corrective actions

• [math]\displaystyle{ ({{\lambda }_{BD}}-\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\lambda }_{i}}) }[/math] is the remaining failure intensity for all unseen BD modes

All [math]\displaystyle{ M }[/math] BD modes observed by test time [math]\displaystyle{ T }[/math] may not be fixed by time [math]\displaystyle{ T }[/math] so the actual failure intensity at time [math]\displaystyle{ T }[/math] may not be [math]\displaystyle{ r(T) }[/math] . However, [math]\displaystyle{ r(T) }[/math] can be viewed as the achieved failure intensity at time [math]\displaystyle{ T }[/math] if all fixes were updated and incorporated into the system. All of the fixes for the BD modes found during the test are incorporated as delayed fixes at the end of the test phase. Therefore, the system failure intensity is constant at [math]\displaystyle{ r(0)={{\lambda }_{A}}+{{\lambda }_{BD}} }[/math] through the test phase and will then jump to a lower value [math]\displaystyle{ r(T) }[/math] after the delayed fixes have been implemented. Let [math]\displaystyle{ {{N}_{A}} }[/math] and [math]\displaystyle{ {{N}_{BD}} }[/math] be the total number of A and BD failures observed during the test [math]\displaystyle{ (0,T) }[/math] and let [math]\displaystyle{ N={{N}_{A}}+{{N}_{BD}} }[/math] . In addition, there are [math]\displaystyle{ M }[/math] distinct BD modes observed during the test. After implementing the [math]\displaystyle{ M }[/math] fixes, the failure intensity for the system at time [math]\displaystyle{ T }[/math] (after the jump) is given by the function [math]\displaystyle{ r(T) }[/math] .
[math]\displaystyle{ r(0) }[/math] is actually the demonstrated failure intensity, which is based on actual system performance of the hardware tested and not of some future configuration. A demonstrated reliability value should be determined at the end of each test phase. The demonstrated failure intensity is:

[math]\displaystyle{ {{\widehat{\lambda }}_{D}}(T)=r(0)=\frac{{{N}_{A}}+{{N}_{BD}}}{T} }[/math]

The demonstrated MTBF is given by:

[math]\displaystyle{ M\widehat{T}B{{F}_{D}}={{[{{\widehat{\lambda }}_{D}}(T)]}^{-1}} }[/math]

The detailed procedure for estimating [math]\displaystyle{ r(T) }[/math] is given in Crow, L.H., An Extended Reliability Growth Model for Managing and Assessing Corective Actions and is reviewed here. Let [math]\displaystyle{ E[\cdot ] }[/math] denote the expected value:

[math]\displaystyle{ E[r(T)]={{\lambda }_{A}}+\underset{i=1}{\overset{K}{\mathop \sum }}\,(1-{{d}_{i}}){{\lambda }_{i}}+\underset{i=1}{\overset{K}{\mathop \sum }}\,{{d}_{i}}{{\lambda }_{i}}{{e}^{-{{\lambda }_{i}}T}} }[/math]

Under realistic assumptions [math]\displaystyle{ E[r(T)] }[/math] also may be expressed as:

[math]\displaystyle{ E[r(T)]={{\lambda }_{A}}+\underset{i=1}{\overset{K}{\mathop \sum }}\,(1-{{d}_{i}}){{\lambda }_{i}}+\overline{d}h(T) }[/math]

where [math]\displaystyle{ \overline{d} }[/math] is the mean effectiveness factor and [math]\displaystyle{ h(T) }[/math] is the instantaneous rate at which a new BD mode will occur at time [math]\displaystyle{ T }[/math] . The maximum likelihood estimate for the [math]\displaystyle{ h(T) }[/math] is:

[math]\displaystyle{ h(T)={{\lambda }_{BD}}{{\beta }_{BD}}{{T}^{{{\beta }_{BD}}-1}} }[/math]

And, [math]\displaystyle{ \overline{d}h(T) }[/math] is the bias term, such that:

[math]\displaystyle{ B(T)=\overline{d}h(T) }[/math]

Estimation of Bias Term

Let [math]\displaystyle{ {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{M}}\lt T }[/math] denote the cumulative test times for the first occurrences of BD modes. Then, the maximum likelihood estimates of [math]\displaystyle{ {{\lambda }_{BD}} }[/math] and [math]\displaystyle{ {{\beta }_{BD}} }[/math] are:

[math]\displaystyle{ {{\hat{\beta }}_{BD}}=\frac{M}{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,\ln \left( \tfrac{T}{{{X}_{i}}} \right)} }[/math]

[math]\displaystyle{ {{\hat{\lambda }}_{BD}}=\frac{M}{{{T}^{{{{\hat{\beta }}}_{BD}}}}} }[/math]

The intensity function [math]\displaystyle{ h(t) }[/math] for [math]\displaystyle{ t\gt 0 }[/math] is estimated by:

[math]\displaystyle{ h(t)={{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{t}^{{{\widehat{\beta }}_{BD}}-1}} }[/math]

In particular, the maximum likelihood estimate for the rate of occurrence for the distinct BD modes at time [math]\displaystyle{ T }[/math] is:

[math]\displaystyle{ \begin{align} & \widehat{h}(T)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & \frac{M{{\widehat{\beta }}_{BD}}}{T} \end{align} }[/math]

Furthermore, the maximum likelihood estimate of the bias term [math]\displaystyle{ B(T) }[/math] is given by:

[math]\displaystyle{ B(T)=\overline{d}\frac{M{{\widehat{\beta }}_{BD}}}{T} }[/math]

The unbiased estimate of [math]\displaystyle{ {{\beta }_{BD}} }[/math] is:

[math]\displaystyle{ {{\bar{\beta }}_{BD}}=\frac{M-1}{M}{{\hat{\beta }}_{BD}} }[/math]

Thus the unbiased estimate of the bias term is given by:

[math]\displaystyle{ B(T)=\overline{d}\frac{M{{{\bar{\beta }}}_{BD}}}{T} }[/math]

The mean [math]\displaystyle{ \overline{d} }[/math] is given by:

[math]\displaystyle{ \overline{d}=\frac{1}{M}\underset{i=1}{\overset{M}{\mathop \sum }}\,{{d}_{i}} }[/math]

Therefore, the projected failure intensity [math]\displaystyle{ r(T) }[/math] is then estimated at the end of the test phase by:

[math]\displaystyle{ \widehat{r}(T)=\left( \frac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T} \right)+\overline{d}\left( \frac{M}{T}{{\overline{\beta }}_{BD}} \right) }[/math]

The projected MTBF is:

[math]\displaystyle{ M\widehat{T}B{{F}_{P}}={{[r(T)]}^{-1}} }[/math]

Reliability Growth Potential

The failure intensity [math]\displaystyle{ r(T) }[/math] will depend on the management strategy that determines the classification of the A and BD failure modes. The engineering effort applied to the corrective actions determines the effectiveness factors. In addition, [math]\displaystyle{ r(T) }[/math] depends on [math]\displaystyle{ h(t) }[/math] , which is the rate at which problem failure modes are being seen during testing. [math]\displaystyle{ h(t) }[/math] drives the opportunity to take corrective actions based on the seen failure modes and it is an important factor in the overall reliability growth rate. The reliability growth potential is the limiting value of [math]\displaystyle{ r(T) }[/math] as [math]\displaystyle{ T }[/math] increases. This limit is the maximum MTBF that can be attained with the current management strategy. The maximum MTBF will be attained when all [math]\displaystyle{ K }[/math] BD modes have been observed and fixed with EFs [math]\displaystyle{ {{d}_{i}} }[/math] . In terms of failure intensity, the growth potential is expressed by the following equation:

[math]\displaystyle{ {{r}_{GP}}={{\lambda }_{A}}+\underset{i=1}{\overset{K}{\mathop \sum }}\,(1-{{d}_{i}}){{\lambda }_{i}} }[/math]

In terms of the MTBF, the growth potential is given by:

[math]\displaystyle{ MTB{{F}_{GP}}=1/{{r}_{GP}} }[/math]

The procedure for estimating the growth potential is as follows. Suppose that the system is tested for a period of time [math]\displaystyle{ T }[/math] and that [math]\displaystyle{ N }[/math] failures have been observed. According to the management strategy, [math]\displaystyle{ {{N}_{A}} }[/math] of these failures are A modes and [math]\displaystyle{ {{N}_{BD}} }[/math] of these failures are BD modes. For the BD modes, there will be [math]\displaystyle{ M }[/math] distinct fixes. As before, [math]\displaystyle{ {{N}_{i}} }[/math] is the total number of failures for the [math]\displaystyle{ {{i}^{th}} }[/math] BD mode and [math]\displaystyle{ {{d}_{i}} }[/math] is the corresponding assigned EF. From this data, the growth potential failure intensity is estimated by:

[math]\displaystyle{ {{\widehat{r}}_{GP}}(T)=\left( \frac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T} \right) }[/math]

The growth potential MTBF is estimated by:

[math]\displaystyle{ M\widehat{T}B{{F}_{GP}}={{[{{\widehat{r}}_{GP}}]}^{-1}} }[/math]

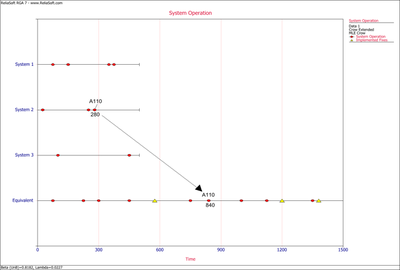
Example: Test-Find-Test Data

Consider the data in the first table below. A system was tested for [math]\displaystyle{ T=400 }[/math] hours. There were a total of [math]\displaystyle{ N=42 }[/math] failures and all corrective actions will be delayed until after the end of the 400 hour test. Each failure has been designated as either an A failure mode (the cause will not receive a corrective action) or a BD mode (the cause will receive a corrective action). There are [math]\displaystyle{ {{N}_{A}}=10 }[/math] A mode failures and [math]\displaystyle{ {{N}_{BD}}=32 }[/math] BD mode failures. In addition, there are [math]\displaystyle{ M=16 }[/math] distinct BD failure modes, which means 16 distinct corrective actions will be incorporated into the system at the end of test. The total number of failures for the [math]\displaystyle{ {{j}^{th}} }[/math] observed distinct BD mode is denoted by [math]\displaystyle{ {{N}_{j}} }[/math] and the total number of BD failures during the test is [math]\displaystyle{ {{N}_{BD}}=\underset{j=1}{\overset{M}{\mathop{\sum }}}\,{{N}_{j}} }[/math] . These values and effectiveness factors are given in the second table.

Determine the projected MTBF and failure intensity.
Determine the growth potential MTBF and failure intensity.
Determine the demonstrated MTBF and failure intensity.

[math]\displaystyle{ i }[/math]	[math]\displaystyle{ {{X}_{i}} }[/math]	Mode	[math]\displaystyle{ i }[/math]	[math]\displaystyle{ {{X}_{i}} }[/math]	Mode
Test-find-test data
1	15	BD1	22	260.1	BD1
2	25.3	BD2	23	263.5	BD8
3	47.5	BD3	24	273.1	A
4	54	BD4	25	274.7	BD6
5	56.4	BD5	26	285	BD13
6	63.6	A	27	304	BD9
7	72.2	BD5	28	315.4	BD4
8	99.6	BD6	29	317.1	A
9	100.3	BD7	30	320.6	A
10	102.5	A	31	324.5	BD12
11	112	BD8	32	324.9	BD10
12	120.9	BD2	33	342	BD5
13	125.5	BD9	34	350.2	BD3
14	133.4	BD10	35	364.6	BD10
15	164.7	BD9	36	364.9	A
16	177.4	BD10	37	366.3	BD2
17	192.7	BD11	38	373	BD8
18	213	A	39	379.4	BD14
19	244.8	A	40	389	BD15
20	249	BD12	41	394.9	A
21	250.8	A	42	395.2	BD16

BD Mode	Number [math]\displaystyle{ {{N}_{j}} }[/math]	First Occurrence	EF [math]\displaystyle{ {{d}_{i}} }[/math]
Effectiveness factors for the unique BD modes
1	2	15.0	.67
2	3	25.3	.72
3	2	47.5	.77
4	2	54.0	.77
5	3	54.0	.87
6	2	99.6	.92
7	1	100.3	.50
8	3	112.0	.85
9	3	125.5	.89
10	4	133.4	.74
11	1	192.7	.70
12	2	249.0	.63
13	1	285.0	.64
14	1	379.4	.72
15	1	389.0	.69
16	1	395.2	.46

Solution

1) From Eqns. (Extend1) and (Extend2), the maximum likelihood estimates of [math]\displaystyle{ {{\beta }_{BD}} }[/math] and [math]\displaystyle{ {{\lambda }_{BD}} }[/math] are determined to be:

[math]\displaystyle{ \begin{align} & {{{\hat{\beta }}}_{BD}}= & \frac{M}{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,\ln (\tfrac{T}{{{X}_{i}}})} \\ & = & 0.7970 \\ & {{{\hat{\lambda }}}_{BD}}= & 0.1350 \end{align} }[/math]

The unbiased estimate of [math]\displaystyle{ \beta }[/math] is:

[math]\displaystyle{ \begin{align} & {{\overline{\beta }}_{BD}}= & \frac{M-1}{M}{{{\hat{\beta }}}_{BD}} \\ & = & 0.7472 \end{align} }[/math]

Based on the test data, [math]\displaystyle{ \overline{d}=\tfrac{1}{M}\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{i}}= }[/math] [math]\displaystyle{ 0.72125 }[/math] . Therefore, [math]\displaystyle{ B(T)=\overline{d}\tfrac{M{{\overline{\beta }}_{BD}}}{T}=0.0215 }[/math] . From Eqn. (extended), the projected failure intensity due to incorporating the 16 corrective actions is:

[math]\displaystyle{ \begin{align} & r(T)= & \left( \frac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T} \right)+\overline{d}\left( \frac{M}{T}{{\overline{\beta }}_{BD}} \right) \\ & = & 0.0661 \end{align} }[/math]

The projected MTBF is:

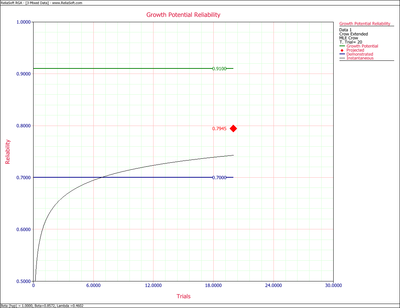
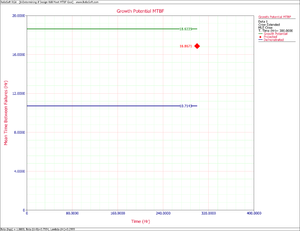
[math]\displaystyle{ M\widehat{T}B{{F}_{P}}={{[r(T)]}^{-1}}=15.127 }[/math]

2) To estimate the maximum reliability that can be attained with this management strategy, use the following calculations.

[math]\displaystyle{ {{N}_{A}}/T=0.0250 }[/math]

[math]\displaystyle{ \frac{1}{T}\underset{i=1}{\overset{16}{\mathop \sum }}\,(1-{{d}_{i}}){{N}_{i}}=0.0196 }[/math]

From Eqn. (extendedGP), the growth potential failure intensity is estimated by:

[math]\displaystyle{ \begin{align} & {{\widehat{r}}_{GP}}(T)= & \left( \frac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T} \right) \\ & = & 0.0250+0.0196 \\ & = & 0.0446 \end{align} }[/math]

The growth potential MTBF is:

[math]\displaystyle{ M\widehat{T}B{{F}_{GP}}={{[{{\widehat{r}}_{GP}}]}^{-1}}=22.4467 }[/math]

3) From Eqn. (extendeddfi), the demonstrated failure intensity and MTBF are estimated by:

[math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{D}}(T)= & \frac{{{N}_{A}}+{{N}_{BD}}}{T} \\ & = & \frac{42}{400} \\ & = & 0.1050 \end{align} }[/math]

[math]\displaystyle{ \begin{align} & M\widehat{T}B{{F}_{D}}= & {{[{{\widehat{\lambda }}_{D}}(T)]}^{-1}} \\ & = & 9.5238 \end{align} }[/math]

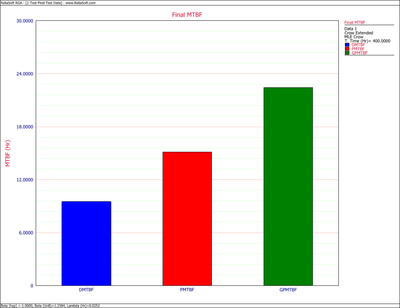
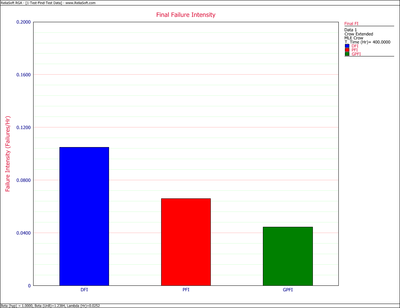
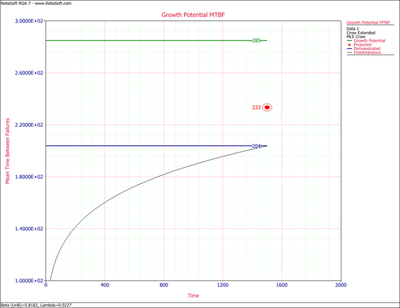
The first chart below shows the demonstrated, projected and growth potential MTBF. The second shows the demonstrated, projected and growth potential failure intensity.

Demonstrated, projected and growth potential MTBF.

Demonstrated, projected and growth potential failure intensity.

Test-Fix-Find-Test

Traditional reliability growth models provide assessments for two types of testing and corrective action strategies: test-fix-test and test-find-test. In test-fix-test, failure modes are found during testing and corrective actions for these modes are incorporated during the test. Data from this type of test can be modeled appropriately with the Crow-AMSAA model, which was discussed in a previous chapter. In test-find-test, modes are found during testing but all of the corrective actions are delayed and incorporated after the completion of the test. Data from this type of test can be modeled appropriately with the Crow-AMSAA Projection model, which was described above in the Test-Find-Test section. However, a common strategy involves a combination of these two approaches, where some corrective actions are incorporated during the test and some corrective actions are delayed and incorporated at the end of the test. This strategy is referred to as test-fix-find-test. Data from this test can be modeled appropriately with the Crow Extended reliability growth model, which is described next.

Recall that B failure modes are all failure modes that will receive a corrective action. In order to provide the assessment and management metric structure for corrective actions during and after a test, two types of B modes are defined. BC failure modes are corrected during the test and BD failure modes are delayed until the end of the test. Type A failure modes are defined as before; i.e. those failure modes that will not receive a corrective action, either during or at the end of the test.

Development of the Crow Extended Model

Let [math]\displaystyle{ {{\lambda }_{BD}} }[/math] denote the constant failure intensity for the BD failure modes and let [math]\displaystyle{ h(t|BD) }[/math] denote the first occurrence function for the BD failure modes. In addition, as before, let [math]\displaystyle{ K }[/math] be the number of BD failure modes, let [math]\displaystyle{ {{d}_{i}} }[/math] be the effectiveness factor for the [math]\displaystyle{ {{i}^{th}} }[/math] BD failure mode and let [math]\displaystyle{ \overline{d} }[/math] be the average effectiveness factor.
The Crow Extended model projected failure intensity is given by:

[math]\displaystyle{ {{\lambda }_{EM}}={{\lambda }_{CA}}-{{\lambda }_{BD}}+\underset{i=1}{\overset{K}{\mathop \sum }}\,(1-{{d}_{i}}){{\lambda }_{i}}+\overline{d}h(T|BD) }[/math]

where [math]\displaystyle{ {{\lambda }_{CA}}=\lambda \beta {{T}^{\beta -1}} }[/math] is the achieved failure intensity at time [math]\displaystyle{ T }[/math] .
The Crow Extended model projected MTBF is:

[math]\displaystyle{ {{M}_{EM}}=1/{{\lambda }_{EM}} }[/math]

This is the MTBF after the delayed fixes have been implemented. Under the extended reliability growth model, the demonstrated failure intensity before the delayed fixes is the first term, [math]\displaystyle{ {{\lambda }_{CA}} }[/math] . The demonstrated MTBF at time [math]\displaystyle{ T }[/math] before the delayed fixes is given by:

[math]\displaystyle{ {{M}_{CA}}\text{ }={{[{{\lambda }_{CA}}]}^{-1}} }[/math]

If you assume that there are no delayed corrective actions (BD modes) then the model reduces to the special case of the Crow-AMSAA model (the first term only in Eqn. (extendl)) and the achieved MTBF equals the projection. That is, there is no jump. If you assume that there are no corrective actions during the test (BC modes) then the model reduces to the test-find-test scenario described in the previous section.

Estimation of the Model

In the general estimation of the Crow Extended model, it is required that all failure times during the test are known. Furthermore, the ID of each A, BC and BD failure mode needs to be entered.
The estimate of the projected failure intensity for the Crow Extended model is given by:

[math]\displaystyle{ {{\widehat{\lambda }}_{EM}}={{\widehat{\lambda }}_{CA}}-{{\widehat{\lambda }}_{BD}}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T}+\overline{d}\widehat{h}(T|BD) }[/math]

where [math]\displaystyle{ {{N}_{i}} }[/math] is the total number of failures for the [math]\displaystyle{ {{i}^{th}} }[/math] BD mode and [math]\displaystyle{ {{d}_{i}} }[/math] is the corresponding assigned EF. In order to obtain the first term, [math]\displaystyle{ {{\widehat{\lambda }}_{CA}} }[/math] , fit all of the data (regardless of mode classification) to the Crow-AMSAA model to estimate [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] , thus:

[math]\displaystyle{ {{\widehat{\lambda }}_{CA}}=\widehat{\lambda }\widehat{\beta }{{T}^{\widehat{\beta }-1}} }[/math]

The remaining terms are analyzed with the Crow Extended model, which is applied to only the BD data.

[math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=\frac{{{N}_{BD}}}{T} }[/math]

[math]\displaystyle{ \begin{align} & \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & \frac{M{{\widehat{\beta }}_{BD}}}{T} \end{align} }[/math]

[math]\displaystyle{ {{\widehat{\beta }}_{BD}} }[/math] is the unbiased estimated of [math]\displaystyle{ \beta }[/math] for the Crow-AMSAA model based on the first occurrence of [math]\displaystyle{ M }[/math] distinct BD modes.
The structure for the Crow Extended model includes the following special data analysis cases:

Test-fix-test with no failure modes known or with BC failure modes known. With this type of data, the Crow Extended model will take the form of the traditional Crow-AMSAA analysis described in a previous chapter.
Test-find-test with BD failure modes known. With this type of data, the Crow Extended model will take the form of the Crow-AMSAA Projection analysis described previously in the Test-Find-Test section.
Test-fix-find-test with BC and BD failure modes known. With this type of data, the full capabilities of the Crow Extended model will be applied, as described in the following sections.

Reliability Growth Potential and Maturity Metrics

The growth potential and some maturity metrics for the Crow Extended model are calculated as follows.
• Initial system MTBF and failure intensity are given by:

[math]\displaystyle{ {{\widehat{M}}_{I}}=\frac{\Gamma \left( 1+\tfrac{1}{\widehat{\beta }} \right)}{{{\widehat{\lambda }}^{\tfrac{1}{\widehat{\beta }}}}} }[/math]

and:

[math]\displaystyle{ {{\widehat{\lambda }}_{I}}={{[{{\widehat{M}}_{I}}]}^{-1}} }[/math]

where [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] are the estimators of the Crow-AMSAA model for all data regardless of the failure mode classification (i.e. A, BC or BD).
• A mode failure intensity and MTBF are given by:

[math]\displaystyle{ {{\widehat{\lambda }}_{A}}=\frac{{{N}_{A}}}{T} }[/math]

[math]\displaystyle{ {{\widehat{M}}_{A}}={{[{{\widehat{\lambda }}_{A}}]}^{-1}} }[/math]

• Initial BD mode failure intensity are given by:

[math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=\frac{{{N}_{BD}}}{T} }[/math]

• BC mode initial failure intensity and MTBF are given by:

[math]\displaystyle{ {{\widehat{\lambda }}_{I(BC)}}={{\widehat{\lambda }}_{I}}-{{\widehat{\lambda }}_{A}}-{{\widehat{\lambda }}_{BD}} }[/math]

[math]\displaystyle{ {{\widehat{M}}_{I(BC)}}={{[{{\widehat{\lambda }}_{I(BC)}}]}^{-1}} }[/math]

• Failure intensity [math]\displaystyle{ h(T|BC) }[/math] and instantaneous MTBF [math]\displaystyle{ M(T|BC) }[/math] for new BC failure modes at the end of test time [math]\displaystyle{ T }[/math] are given by:

[math]\displaystyle{ \widehat{h}(T|BC)=\widehat{\lambda }\widehat{\beta }{{T}^{\widehat{\beta }-1}} }[/math]

[math]\displaystyle{ \widehat{M}(T|BC)={{[\widehat{h}(T|BC)]}^{-1}} }[/math]

where [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] are the estimators of the Crow-AMSAA model for the first occurrence of distinct BC modes.
• Average effectiveness factor for BC failure modes is given by:

[math]\displaystyle{ {{\widehat{d}}_{BC}}=\frac{\left[ \tfrac{N_{BC}^{\left( \tfrac{1}{{{{\hat{\beta }}}_{BC}}} \right)}}{\Gamma \left( 1+\tfrac{1}{{{{\hat{\beta }}}_{BC}}} \right)} \right]-{{N}_{BC}}}{\left[ \tfrac{N_{BC}^{\left( \tfrac{1}{{{{\hat{\beta }}}_{BC}}} \right)}}{\Gamma \left( 1+\tfrac{1}{{{{\hat{\beta }}}_{BC}}} \right)} \right]-{{M}_{BC}}} }[/math]

where [math]\displaystyle{ {{N}_{BC}} }[/math] is the total number of observed BC modes, [math]\displaystyle{ {{M}_{BC}} }[/math] is the number of unique BC modes and [math]\displaystyle{ {{\hat{\beta }}_{BC}} }[/math] is the MLE for the first occurrence of distinct BC modes. If [math]\displaystyle{ {{\hat{\beta }}_{BC}}\ge 1 }[/math] then [math]\displaystyle{ {{\widehat{d}}_{BC}} }[/math] equals zero.
• Growth potential failure intensity and growth potential MTBF are given by:

[math]\displaystyle{ {{\widehat{\lambda }}_{GP}}={{\widehat{\lambda }}_{CA}}-{{\widehat{\lambda }}_{BD}}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T} }[/math]

[math]\displaystyle{ {{\widehat{M}}_{GP}}={{[{{\widehat{\lambda }}_{GP}}]}^{-1}} }[/math]

Failure Mode Management Strategy

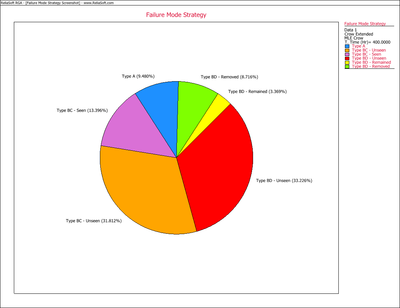
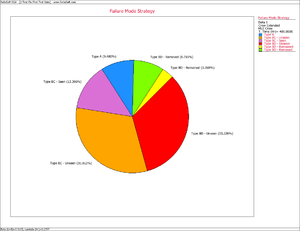
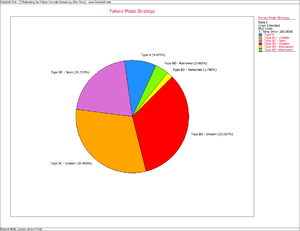
Management controls the resources for corrective actions. Consequently, the effectiveness factors are part of the management strategy. For the BD mode failure intensity that has been seen during development testing, 100 [math]\displaystyle{ d }[/math] percent will be removed and 100 [math]\displaystyle{ (1-d) }[/math] percent will remain in the system. Therefore, after the corrective actions have been made, the current system instantaneous failure intensity consists of the failure intensity due to the A modes plus the failure intensity for the unseen BC modes, plus the failure intensity for the unseen BD modes, plus the failure intensity for the BD modes that have been seen. The following pie chart shows how the system's instantaneous failure intensity can be broken down into its individual pieces based on the current failure mode strategy.

System failure intensity after the corrective actions.

Keep in mind that the individual components of the system's instantaneous failure intensity will depend on the classifications defined in the data. For example, if BC modes are not present within the data then the BC mode MTBF will not be a part of the overall system MTBF. The individual pieces of the pie, as shown Figure extendedpic4, are calculated using the following equations.

Let:

[math]\displaystyle{ \hat{r}(T)=\hat{\lambda }\hat{\beta }{{T}^{\hat{\beta }-1}} }[/math]

where [math]\displaystyle{ T }[/math] is the test time and [math]\displaystyle{ \hat{\beta } }[/math] and [math]\displaystyle{ \hat{\lambda } }[/math] are the maximum likelihood estimates of the Crow-AMSAA model for all of the data. [math]\displaystyle{ \hat{\beta } }[/math] is the biased estimate of [math]\displaystyle{ \beta }[/math] . Therefore:

[math]\displaystyle{ \hat{\beta }=\frac{N}{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,\ln \left( \tfrac{T}{{{X}_{i}}} \right)} }[/math]

[math]\displaystyle{ \hat{\lambda }=\frac{N}{{{T}^{{\hat{\beta }}}}} }[/math]

where [math]\displaystyle{ N }[/math] is the total number of failures and [math]\displaystyle{ {{X}_{i}} }[/math] is the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure. Let the successive failures [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{3}}\lt {{X}_{N}} }[/math] be partitioned into the A mode failures ( [math]\displaystyle{ {{N}_{A}} }[/math] ), BC first occurrence failures ( [math]\displaystyle{ {{N}_{BCF}} }[/math] ), BC remaining failures ( [math]\displaystyle{ {{N}_{BCR}} }[/math] ), BD first occurrence failure ( [math]\displaystyle{ {{N}_{BDF}} }[/math] ) and the BD remaining failures ( [math]\displaystyle{ {{N}_{BDR}} }[/math] ). For continuous data, each portion of the pie chart due to each of the modes is calculated as follows:

• A modes

[math]\displaystyle{ A=\left( \frac{T}{{{N}^{2}}} \right)\left[ \underset{i=1}{\overset{{{N}_{A}}}{\mathop \sum }}\,\ln \left( \frac{T}{{{X}_{Ai}}} \right) \right]\hat{r}(T) }[/math]

• BC modes unseen

[math]\displaystyle{ B{{C}_{unseen}}=\left( \frac{T}{{{N}^{2}}} \right)\left[ \underset{i=1}{\overset{{{N}_{BCF}}}{\mathop \sum }}\,\ln \left( \frac{T}{{{X}_{BCFi}}} \right) \right]\hat{r}(T) }[/math]

• BC modes seen

[math]\displaystyle{ B{{C}_{seen}}=\left( \frac{T}{{{N}^{2}}} \right)\left[ \underset{i=1}{\overset{{{N}_{BCR}}}{\mathop \sum }}\,\ln \left( \frac{T}{{{X}_{BCRi}}} \right) \right]\hat{r}(T) }[/math]

• BD modes unseen

[math]\displaystyle{ B{{D}_{unseen}}=\left( \frac{T}{{{N}^{2}}} \right)\left[ \underset{i=1}{\overset{{{N}_{BDF}}}{\mathop \sum }}\,\ln \left( \frac{T}{{{X}_{BDFi}}} \right) \right]\hat{r}(T) }[/math]

• BD modes seen

[math]\displaystyle{ B{{D}_{seen}}=\left( \frac{T}{{{N}^{2}}} \right)\left[ \underset{i=1}{\overset{{{N}_{BDR}}}{\mathop \sum }}\,\ln \left( \frac{T}{{{X}_{BDRi}}} \right) \right]\hat{r}(T) }[/math]

• BD modes remain

[math]\displaystyle{ \begin{align} & B{{D}_{remain}}= & \left( 1-\frac{1}{M}\underset{i=1}{\overset{M}{\mathop \sum }}\,{{d}_{i}} \right)\cdot B{{D}_{seen}} \\ & = & \left( 1-\overline{d} \right)\cdot B{{D}_{seen}} \end{align} }[/math]

• BD modes removed

[math]\displaystyle{ \begin{align} & B{{D}_{removed}}= & \frac{1}{M}\underset{i=1}{\overset{M}{\mathop \sum }}\,{{d}_{i}}\cdot B{{D}_{seen}} \\ & = & \overline{d}\cdot B{{D}_{seen}} \end{align} }[/math]

For grouped data, from Chapter 5 the maximum likelihood estimates of [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \lambda }[/math] are calculated such that the following equations are satisfied:

[math]\displaystyle{ \underset{i=1}{\overset{K}{\mathop \sum }}\,{{N}_{i}}\left[ \frac{t_{i}^{{\hat{\beta }}}\ln ({{t}_{i}})-t_{i-1}^{{\hat{\beta }}}\ln ({{t}_{i-1}})}{t_{i}^{{\hat{\beta }}}-t_{i-1}^{{\hat{\beta }}}}-\ln T \right]=0 }[/math]

[math]\displaystyle{ \hat{\lambda }=\frac{N}{T_{K}^{{\hat{\beta }}}} }[/math]

where [math]\displaystyle{ K }[/math] is the number of groups and [math]\displaystyle{ N=\underset{i=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{i}} }[/math] .

• A modes

[math]\displaystyle{ A=\left( \frac{T}{{{N}^{2}}} \right)\left[ {{N}_{A}}\ln (T)-\underset{i=1}{\overset{K}{\mathop \sum }}\,\frac{{{N}_{Ai}}}{{\hat{\beta }}}\left( \frac{t_{i}^{{\hat{\beta }}}\ln (t_{i}^{{\hat{\beta }}})-t_{i-1}^{{\hat{\beta }}}\ln (t_{i-1}^{{\hat{\beta }}})}{t_{i}^{{\hat{\beta }}}-t_{i-1}^{{\hat{\beta }}}}-1 \right) \right]\hat{r}(T) }[/math]

• BC modes unseen

[math]\displaystyle{ B{{C}_{unseen}}=\left( \frac{T}{{{N}^{2}}} \right)\left[ {{N}_{BCF}}\ln (T)-\underset{i=1}{\overset{K}{\mathop \sum }}\,\frac{{{N}_{BCFi}}}{{\hat{\beta }}}\left( \frac{t_{i}^{{\hat{\beta }}}\ln (t_{i}^{{\hat{\beta }}})-t_{i-1}^{{\hat{\beta }}}\ln (t_{i-1}^{{\hat{\beta }}})}{t_{i}^{{\hat{\beta }}}-t_{i-1}^{{\hat{\beta }}}}-1 \right) \right]\hat{r}(T) }[/math]

• BC modes seen

[math]\displaystyle{ B{{C}_{seen}}=\left( \frac{T}{{{N}^{2}}} \right)\left[ {{N}_{BCR}}\ln (T)-\underset{i=1}{\overset{K}{\mathop \sum }}\,\frac{{{N}_{BCRi}}}{{\hat{\beta }}}\left( \frac{t_{i}^{{\hat{\beta }}}\ln (t_{i}^{{\hat{\beta }}})-t_{i-1}^{{\hat{\beta }}}\ln (t_{i-1}^{{\hat{\beta }}})}{t_{i}^{{\hat{\beta }}}-t_{i-1}^{{\hat{\beta }}}}-1 \right) \right]\hat{r}(T) }[/math]

• BD modes unseen

[math]\displaystyle{ B{{D}_{unseen}}=\left( \frac{T}{{{N}^{2}}} \right)\left[ {{N}_{BDF}}\ln (T)-\underset{i=1}{\overset{K}{\mathop \sum }}\,\frac{{{N}_{BDFi}}}{{\hat{\beta }}}\left( \frac{t_{i}^{{\hat{\beta }}}\ln (t_{i}^{{\hat{\beta }}})-t_{i-1}^{{\hat{\beta }}}\ln (t_{i-1}^{{\hat{\beta }}})}{t_{i}^{{\hat{\beta }}}-t_{i-1}^{{\hat{\beta }}}}-1 \right) \right]\hat{r}(T) }[/math]

• BD modes seen

[math]\displaystyle{ B{{D}_{seen}}=\left( \frac{T}{{{N}^{2}}} \right)\left[ {{N}_{BDR}}\ln (T)-\underset{i=1}{\overset{K}{\mathop \sum }}\,\frac{{{N}_{BDRi}}}{{\hat{\beta }}}\left( \frac{t_{i}^{{\hat{\beta }}}\ln (t_{i}^{{\hat{\beta }}})-t_{i-1}^{{\hat{\beta }}}\ln (t_{i-1}^{{\hat{\beta }}})}{t_{i}^{{\hat{\beta }}}-t_{i-1}^{{\hat{\beta }}}}-1 \right) \right]\hat{r}(T) }[/math]

• BD modes remain

[math]\displaystyle{ \begin{align} & B{{D}_{remain}}= & \left( 1-\frac{1}{M}\underset{i=1}{\overset{M}{\mathop \sum }}\,{{d}_{i}} \right)\cdot B{{D}_{seen}} \\ & = & \left( 1-\overline{d} \right)\cdot B{{D}_{seen}} \end{align} }[/math]

• BD modes removed

[math]\displaystyle{ \begin{align} & B{{D}_{removed}}= & \frac{1}{M}\underset{i=1}{\overset{M}{\mathop \sum }}\,{{d}_{i}}\cdot B{{D}_{seen}} \\ & = & \overline{d}\cdot B{{D}_{seen}} \end{align} }[/math]

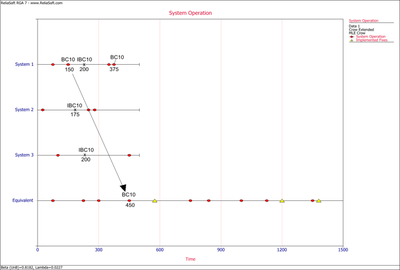
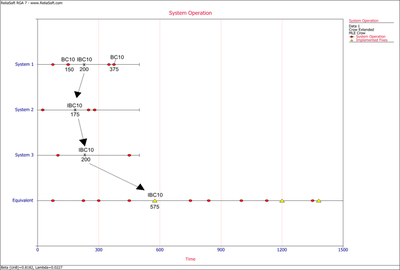
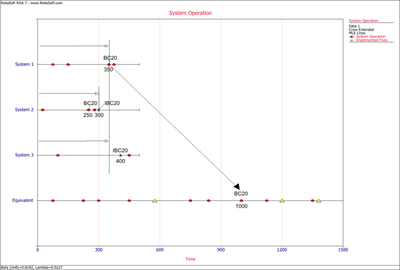
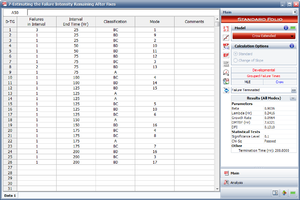
Example: Test-Fix-Find-Test Data

Consider the data given in the first table below. There were 56 total failures and [math]\displaystyle{ T=400 }[/math] . The effectiveness factors of the unique BD modes are given in the second table. Determine the following:

Calculate the demonstrated MTBF and failure intensity.
Calculate the projected MTBF and failure intensity.
What is the rate at which unique BD modes are being generated during this test?
If the test continues for an additional 50 hours, what is the minimum number of new unique BD modes expected to be generated?

[math]\displaystyle{ i\,\! }[/math]	[math]\displaystyle{ {{X}_{i}}\,\! }[/math]	Mode	[math]\displaystyle{ i\,\! }[/math]	[math]\displaystyle{ {{X}_{i}}\,\! }[/math]	Mode
Test-Fix-Find-Test Data
1	0.7	BC17	29	192.7	BD11
2	3.7	BC17	30	213	A
3	13.2	BC17	31	244.8	A
4	15	BD1	32	249	BD12
5	17.6	BC18	33	250.8	A
6	25.3	BD2	34	260.1	BD1
7	47.5	BD3	35	263.5	BD8
8	54	BD4	36	273.1	A
9	54.5	BC19	37	274.7	BD6
10	56.4	BD5	38	282.8	BC27
11	63.6	A	39	285	BD13
12	72.2	BD5	40	304	BD9
13	99.2	BC20	41	315.4	BD4
14	99.6	BD6	42	317.1	A
15	100.3	BD7	43	320.6	A
16	102.5	A	44	324.5	BD12
17	112	BD8	45	324.9	BD10
18	112.2	BC21	46	342	BD5
19	120.9	BD2	47	350.2	BD3
20	121.9	BC22	48	355.2	BC28
21	125.5	BD9	49	364.6	BD10
22	133.4	BD10	50	364.9	A
23	151	BC23	51	366.3	BD2
24	163	BC24	52	373	BD8
25	164.7	BD9	53	379.4	BD14
26	174.5	BC25	54	389	BD15
27	177.4	BD10	55	394.9	A
28	191.6	BC26	56	395.2	BD16

BD Mode	EF [math]\displaystyle{ {{d}_{i}} }[/math]
Effectiveness factors for the unique BD modes
1	.67
2	.72
3	.77
4	.77
5	.87
6	.92
7	.50
8	.85
9	.89
10	.74
11	.70
12	.63
13	.64
14	.72
15	.69
16	.46

Solution

1) In order to obtain [math]\displaystyle{ {{\widehat{\lambda }}_{CA}} }[/math] , use the traditional Crow-AMSAA model for test-fix-test to fit all 56 data points, regardless of the failure mode classification to get:

[math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.91026 \\ & \widehat{\lambda }= & 0.23969 \end{align} }[/math]

Thus the achieved or demonstrated failure intensity is estimated by:

[math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{CA}}= & \widehat{\lambda }\widehat{\beta }{{T}^{\widehat{\beta }-1}} \\ & = & 0.23969\times 0.91026\times {{400}^{(0.91026-1)}} \\ & = & 0.12744 \end{align} }[/math]

The achieved or demonstrated MTBF, [math]\displaystyle{ {{M}_{CA}} }[/math] , is the system reliability attained at the end of test, [math]\displaystyle{ T=400 }[/math] , and is estimated by:

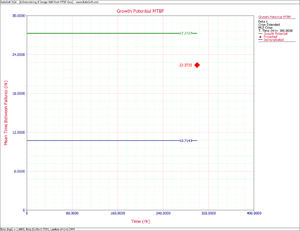
[math]\displaystyle{ {{\widehat{M}}_{CA}}={{[{{\widehat{\lambda }}_{CA}}]}^{-1}}=7.84708 }[/math]

2) For this data set, [math]\displaystyle{ M=16 }[/math] and [math]\displaystyle{ T=400 }[/math] .

[math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=\frac{{{N}_{BD}}}{T}=\frac{32}{400}=0.08 }[/math]

[math]\displaystyle{ \overline{d}=\underset{i=1}{\overset{M}{\mathop \sum }}\,{{d}_{i}}/M=0.72125 }[/math]

[math]\displaystyle{ \underset{i=1}{\overset{16}{\mathop \sum }}\,(1-{{d}_{i}}){{N}_{i}}/T=0.01955 }[/math]

Calculate [math]\displaystyle{ \hat{\beta } }[/math] and [math]\displaystyle{ \hat{\lambda } }[/math] of the BD modes using Eqns. (Extend1) and (Extend2):

[math]\displaystyle{ \begin{align} & {{{\hat{\beta }}}_{BD}}= & 0.74715 \\ & {{{\hat{\lambda }}}_{BD}}= & 0.18197 \end{align} }[/math]

Then:

[math]\displaystyle{ \overline{d}\widehat{h}(T|BD)=0.0215 }[/math]

Therefore:

[math]\displaystyle{ \begin{align} 43) & {{\widehat{\lambda }}_{EM}}= & {{\widehat{\lambda }}_{CA}}-{{\widehat{\lambda }}_{BD}}+\underset{i=1}{\overset{K}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T}+\overline{d}\widehat{h}(T|BD) \\ & = & 0.12744-0.08+0.0196+0.0215 \\ & = & 0.08854 \end{align} }[/math]

The Crow Extended model projected MTBF is:

[math]\displaystyle{ \begin{align} & {{\widehat{M}}_{EM}}= & {{[{{\widehat{\lambda }}_{EM}}]}^{-1}} \\ & = & 11.29418 \end{align} }[/math]

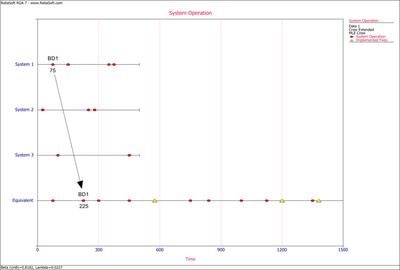
Consequently, based on the Crow Extended model and the data in Tables 9.3 and 9.4, the MTBF grew to 7.85 as a result of the corrective actions for the BC failure modes during the test. The MTBF then jumped to 11.29 after the test as a result of the delayed corrective actions for the BD failure modes. The management strategy can be summarized by the Failure Mode Strategy plot shown next.

Failure Mode Strategy plot.

This pie chart shows that 9.48% of the system's failure intensity has been left in (A modes), 31.81% of the failure intensity due to the BC modes has not been seen yet and 13.40% was removed during the test (BC modes - seen). In addition, 33.23% of the failure intensity due to the BD modes has not been seen yet, 3.37% will remain in the system since the corrective actions will not be completely effective at eliminating the identified failure modes and 8.72% will be removed after the delayed corrective actions.

3) The rate at which unique BD modes are being generated is equal to [math]\displaystyle{ h{{(T|BD)}^{-1}} }[/math] , where:

[math]\displaystyle{ \begin{align} & h{{(T|BD)}^{-1}}= & \frac{1}{{{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}}} \\ & = & \frac{T}{M{{\widehat{\beta }}_{BD}}} \\ & = & 33.4605 \end{align} }[/math]

4) Unique BD modes are being generated every 33.4605 hours. If the test continues for another 50 hours, then at least one new unique BD mode would be expected to be seen from this additional testing.

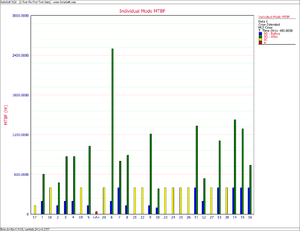
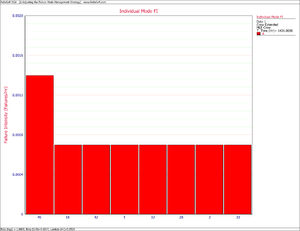
As shown in the next figure, the MTBF of each individual failure mode can be plotted and the failure modes with the lowest MTBF can be identified. These are the failure modes that cause the majority of the system failures.

Individual Mode MTBF chart.

Confidence Bounds

In this section, we will present the methods used in the RGA software to estimate the confidence bounds for the Crow Extended model when applied to developmental testing data. The software provides two methods to estimate the confidence bounds on demonstrated MTBF and failure intensity, projected MTBF and failure intensity and growth potential MTBF and failure intensity. The two methods are the Fisher Matrix (FM) method and Crow bounds. The Fisher Matrix approach is based on the Fisher Information Matrix and is commonly employed in the reliability field. The Crow bounds were developed by Dr. Larry Crow.

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images, more targeted search and the latest content available as a PDF. As of September 2023, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest reference at help.reliasoft.com/reference/reliability_growth_and_repairable_system_analysis

Chapter Appendix D: Crow Extended

Chapter Appendix D

Crow Extended

Available Software:
RGA

More Resources:
RGA examples

In this appendix, we will present the two methods used in the RGA software to estimate the confidence bounds for the Crow extended model when applied to developmental testing data. The Fisher Matrix approach is based on the Fisher Information Matrix and is commonly employed in the reliability field. The Crow bounds were developed by Dr. Larry Crow.

Bounds on Demonstrated Failure Intensity

Fisher Matrix Bounds

If there are no BC failure modes, the demonstrated failure intensity is

[math]\displaystyle{ {{\widehat{\lambda }}_{D}}(T)=\tfrac{{{N}_{A}}+{{N}_{BD}}}{T}\,\! }[/math].

Thus:

[math]\displaystyle{ Var({{\hat{\lambda }}_{D}}(t))=\frac{{{N}_{A}}}{{{T}^{2}}}+\frac{{{N}_{BD}}}{{{T}^{2}}}=\frac{{{\lambda }_{D}}(t)}{T}\,\! }[/math]

and:

[math]\displaystyle{ \sqrt{T}\left( \frac{{{{\hat{\lambda }}}_{D}}(T)-{{\lambda }_{D}}(T)}{\sqrt{{{\lambda }_{D}}(T)}} \right)\sim N(0,1)\,\! }[/math]

[math]\displaystyle{ {{\lambda }_{D}}(T)={{\hat{\lambda }}_{D}}(T)+\frac{{{C}^{2}}}{2}\pm \sqrt{{{{\hat{\lambda }}}_{D}}(T){{C}^{2}}+\frac{{{C}^{4}}}{4}}\,\! }[/math]

where [math]\displaystyle{ C=\tfrac{{{z}_{1-\alpha /2}}}{\sqrt{T}}\,\! }[/math].

If there are BC failure modes, the demonstrated failure intensity, [math]\displaystyle{ {{\widehat{\lambda }}_{D}}(T)={{\widehat{\lambda }}_{CA}}\,\! }[/math], is actually the instantaneous failure intensity based on all of the data. [math]\displaystyle{ {{\lambda }_{CA}}(T)\,\! }[/math] must be positive; thus, [math]\displaystyle{ \ln {{\lambda }_{CA}}(T)\,\! }[/math] is approximately treated as being normally distributed.

[math]\displaystyle{ \frac{\ln {{{\hat{\lambda }}}_{CA}}(T)-\ln {{\lambda }_{CA}}(T)}{\sqrt{Var(\ln {{{\hat{\lambda }}}_{CA}}(T)})}\sim N(0,1)\,\! }[/math]

The approximate confidence bounds on the instantaneous failure intensity are then estimated from:

[math]\displaystyle{ CB={{\hat{\lambda }}_{CA}}(T){{e}^{\pm {{z}_{\alpha }}\sqrt{Var({{{\hat{\lambda }}}_{CA}}(T))}/{{{\hat{\lambda }}}_{CA}}(T)}}\,\! }[/math]

where [math]\displaystyle{ {{\lambda }_{CA}}(t)=\lambda \beta {{T}^{\beta -1}}\,\! }[/math].

[math]\displaystyle{ \begin{align} Var({{{\hat{\lambda }}}_{CA}}(T))= & {{\left( \frac{\partial {{\lambda }_{CA}}(T)}{\partial \beta } \right)}^{2}}Var(\hat{\beta })+{{\left( \frac{\partial {{\lambda }_{CA}}(T)}{\partial \lambda } \right)}^{2}}Var(\hat{\lambda }) \\ & +2\left( \frac{\partial {{\lambda }_{CA}}(T)}{\partial \beta } \right)\left( \frac{\partial {{\lambda }_{CA}}(T)}{\partial \lambda } \right)cov(\hat{\beta },\hat{\lambda }) \end{align}\,\! }[/math]

The variance calculation is the same as described in the Crow-AMSAA Confidence Bounds appendix.

Crow Bounds

If there are no BC failure modes then:

[math]\displaystyle{ \begin{align} {{[{{\lambda }_{D}}(T)]}_{l}}= & {{\widehat{\lambda }}_{D}}(T)\frac{\chi _{(2N,1-\alpha /2)}^{2}}{2N} \\ {{[{{\lambda }_{D}}(T)]}_{u}}= & {{\widehat{\lambda }}_{D}}(T)\frac{\chi _{(2N,\alpha /2)}^{2}}{2N} \end{align}\,\! }[/math]

where [math]\displaystyle{ {{\widehat{\lambda }}_{D}}(T)={{\widehat{\lambda }}_{CA}}\,\! }[/math].

If there are BC modes then the confidence bounds on the demonstrated failure intensity are calculated as presented in the Crow-AMSAA Confidence Bounds appendix.

Bounds on Demonstrated MTBF

Fisher Matrix Bounds

[math]\displaystyle{ \begin{align} & MTB{{F}_{{{D}_{L}}}}= & \frac{1}{{{[{{\lambda }_{D}}(T)]}_{U}}} \\ & MTB{{F}_{{{D}_{U}}}}= & \frac{1}{{{[{{\lambda }_{D}}(T)]}_{L}}} \end{align}\,\! }[/math]

where [math]\displaystyle{ {{[{{\lambda }_{D}}(T)]}_{L}}\,\! }[/math] and [math]\displaystyle{ {{[{{\lambda }_{D}}(T)]}_{U}}\,\! }[/math] can be obtained from the equation given above for Bounds on Demonstrated Failure Intensity.

Crow Bounds

[math]\displaystyle{ \begin{align} MTB{{F}_{{{D}_{L}}}}= & \frac{1}{{{[{{\lambda }_{D}}(T)]}_{U}}} \\ MTB{{F}_{{{D}_{U}}}}= & \frac{1}{{{[{{\lambda }_{D}}(T)]}_{L}}} \end{align}\,\! }[/math]

where [math]\displaystyle{ {{[{{\lambda }_{D}}(T)]}_{L}}\,\! }[/math] and [math]\displaystyle{ {{[{{\lambda }_{D}}(T)]}_{U}}\,\! }[/math] can be obtained from the equation given above for Bounds on Demonstrated Failure Intensity.

Bounds on Projected Failure Intensity

Fisher Matrix Bounds

The projected failure intensity [math]\displaystyle{ {{\lambda }_{P}}(T)\,\! }[/math] must be positive; thus, [math]\displaystyle{ \ln {{\lambda }_{P}}(T)\,\! }[/math] is approximately treated as being normally distributed as well:

[math]\displaystyle{ \frac{\ln {{{\hat{\lambda }}}_{P}}(T)-\ln {{\lambda }_{P}}(t)}{\sqrt{Var(\ln {{{\hat{\lambda }}}_{P}}(T)})}\sim N(0,1)\,\! }[/math]

[math]\displaystyle{ CB={{\hat{\lambda }}_{P}}(T){{e}^{\pm {{z}_{\alpha }}\sqrt{Var({{{\hat{\lambda }}}_{P}}(T))}/{{{\hat{\lambda }}}_{P}}(T)}}\,\! }[/math]

where:

[math]\displaystyle{ {{\hat{\lambda }}_{P}}(T)=\tfrac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,(1-{{d}_{i}})\tfrac{{{N}_{i}}}{T}+\overline{d}\tfrac{M}{T}\bar{\beta }\,\! }[/math] when there are no BC modes.
[math]\displaystyle{ {{\hat{\lambda }}_{P}}(T)={{\widehat{\lambda }}_{EM}}={{\widehat{\lambda }}_{CA}}-{{\widehat{\lambda }}_{BD}}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,(1-{{d}_{i}})\tfrac{{{N}_{i}}}{T}+\overline{d}\widehat{h}(T|BD)\,\! }[/math] when there are BC modes.
[math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the total failure number of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] distinct BD mode.

You can then get:

[math]\displaystyle{ Var({{\lambda }_{P}}(T))\approx Var({{\hat{\gamma }}_{GP}})+\mu _{d}^{2}Var(h(T))\approx \frac{{{{\hat{r}}}_{GP}}}{T}+\mu _{d}^{2}Var(h(T))\,\! }[/math]

where:

[math]\displaystyle{ \begin{align} \hat{h}(T)= & \frac{M}{T}\bar{\beta } \\ Var(\hat{h}(T))= & {{(\frac{M}{T})}^{2}}Var(\bar{\beta })={{(\frac{M}{T})}^{2}}{{(\frac{M}{M-1})}^{2}}Var(\hat{\beta })=\frac{{{M}^{4}}}{{{T}^{2}}{{(M-1)}^{2}}}Var(\hat{\beta }) \end{align}\,\! }[/math]

The [math]\displaystyle{ Var(\hat{\beta })\,\! }[/math] can be obtained from Fisher Matrix based on [math]\displaystyle{ M\,\! }[/math] distinct BD modes.

Crow Bounds

[math]\displaystyle{ \begin{align} {{[{{\lambda }_{P}}(T)]}_{L}}= & {{{\hat{\lambda }}}_{P}}(T)+\frac{{{C}^{2}}}{2}-\sqrt{{{{\hat{\lambda }}}_{P}}(T)\cdot {{C}^{2}}+\frac{{{C}^{4}}}{4}} \\ {{[{{\lambda }_{P}}(T)]}_{U}}= & {{{\hat{\lambda }}}_{P}}(T)+\frac{{{C}^{2}}}{2}+\sqrt{{{{\hat{\lambda }}}_{P}}(T)\cdot \ \,{{C}^{2}}+\frac{{{C}^{4}}}{4}} \end{align}\,\! }[/math]

where [math]\displaystyle{ C=\tfrac{{{z}_{1-\alpha /2}}}{\sqrt{T}}\,\! }[/math].

Bounds on Projected MTBF

Fisher Matrix Bounds

[math]\displaystyle{ \begin{align} MTB{{F}_{{{P}_{L}}}}= & \frac{1}{{{[{{\lambda }_{P}}(T)]}_{U}}} \\ MTB{{F}_{{{P}_{U}}}}= & \frac{1}{{{[{{\lambda }_{P}}(T)]}_{L}}} \end{align}\,\! }[/math]

[math]\displaystyle{ {{[{{\lambda }_{P}}(T)]}_{U}}\,\! }[/math] and [math]\displaystyle{ {{[{{\lambda }_{P}}(T)]}_{L}}\,\! }[/math] can be obtained from the equation given above for Bounds on Projected Failure Intensity.

Crow Bounds

[math]\displaystyle{ \begin{align} MTB{{F}_{{{P}_{L}}}}= & \frac{1}{{{[{{\lambda }_{P}}(T)]}_{U}}} \\ MTB{{F}_{{{P}_{U}}}}= & \frac{1}{{{[{{\lambda }_{P}}(T)]}_{L}}} \end{align}\,\! }[/math]

[math]\displaystyle{ {{[{{\lambda }_{P}}(T)]}_{U}}\,\! }[/math] and [math]\displaystyle{ {{[{{\lambda }_{P}}(T)]}_{L}}\,\! }[/math] can be obtained from the equation given above for Bounds on Projected Failure Intensity.

Bounds on Growth Potential Failure Intensity

Fisher Matrix Bounds

If there are no BC failure modes, the growth potential failure intensity is

[math]\displaystyle{ {{\widehat{r}}_{GP}}(T)=\tfrac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,(1-{{d}_{i}})\tfrac{{{N}_{i}}}{T}\,\! }[/math].

Then:

[math]\displaystyle{ \begin{align} Var({{\widehat{r}}_{GP}})= & \frac{1}{T}\left[ \frac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{(1-{{d}_{i}})}^{2}}\frac{{{N}_{i}}}{T} \right] \\ \le & \frac{1}{T}\left[ \frac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T} \right] \\ = & \frac{{{r}_{GP}}}{T} \end{align}\,\! }[/math]

If there are BC failure modes, the growth potential failure intensity is

[math]\displaystyle{ {{\widehat{r}}_{GP}}(T)={{\widehat{\lambda }}_{CA}}-{{\widehat{\lambda }}_{BD}}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,(1-{{d}_{i}})\tfrac{{{N}_{i}}}{T},\,\! }[/math] [math]\displaystyle{ Var({{\widehat{r}}_{GP}})\approx \tfrac{{{r}_{GP}}}{T}\,\! }[/math].

Therefore:

[math]\displaystyle{ \sqrt{T}\left( \frac{{{{\hat{r}}}_{GP}}-{{r}_{GP}}}{\sqrt{{{r}_{GP}}}} \right)\sim N(0,1)\,\! }[/math]

The confidence bounds on the growth potential failure intensity are as follows:

[math]\displaystyle{ \begin{align} {{r}_{L}}= & {{{\hat{r}}}_{GP}}+\frac{{{C}^{2}}}{2}-\sqrt{{{{\hat{r}}}_{GP}}\,{{C}^{2}}+\frac{{{C}^{4}}}{4}} \\ {{r}_{U}}= & {{{\hat{r}}}_{GP}}+\frac{{{C}^{2}}}{2}+\sqrt{{{{\hat{r}}}_{GP}}\,{{C}^{2}}+\frac{{{C}^{4}}}{4}} \end{align}\,\! }[/math]

where [math]\displaystyle{ C=\tfrac{{{z}_{1-\alpha /2}}}{\sqrt{T}}\,\! }[/math].

Crow Bounds

The Crow bounds for the growth potential failure intensity are the same as the Fisher Matrix bounds.

Bounds on Growth Potential MTBF

Fisher Matrix Bounds

[math]\displaystyle{ \begin{align} MTB{{F}_{G{{P}_{L}}}}= & \frac{1}{{{r}_{U}}} \\ MTB{{F}_{G{{P}_{U}}}}= & \frac{1}{{{r}_{L}}} \end{align}\,\! }[/math]

where [math]\displaystyle{ {{r}_{U}}\,\! }[/math] and [math]\displaystyle{ {{r}_{L}}\,\! }[/math] can be obtained from the equation given above for Bounds on Growth Potential Failure Intensity.

Crow Bounds

The Crow bounds for the growth potential MTBF are the same as the Fisher Matrix bounds.