Repairable Systems Analysis Reference Example
From ReliaWiki
Revision as of 23:22, 12 June 2014 by Beth Ann Paape (talk | contribs)
RGA_Reference_Examples_Banner.png
|
RGA_Reference_Examples |
This example compares the results for a repairable systems analysis.
Reference Case
Crow, L.H., Reliability Analysis for Complex Repairable Systems, Reliability and Biometry: Statistical Analysis of Lifelength, pg. 385, 1974.
Data
| System 1 | System 2 | System 3 |
|---|---|---|
| 4.3 | 0.1 | 8.4 |
| 4.4 | 5.6 | 32.4 |
| 10.2 | 18.6 | 44.7 |
| 23.5 | 19.5 | 48.4 |
| 23.8 | 24.2 | 50.6 |
| 26.4 | 26.7 | 73.6 |
| 74 | 45.1 | 98.7 |
| 77.1 | 45.8 | 112.2 |
| 92.1 | 72.7 | 129.8 |
| 197.2 | 75.7 | 136 |
| 98.6 | 195.8 | |
| 120.1 | ||
| 161.8 | ||
| 180.6 | ||
| 190.8 |
Result
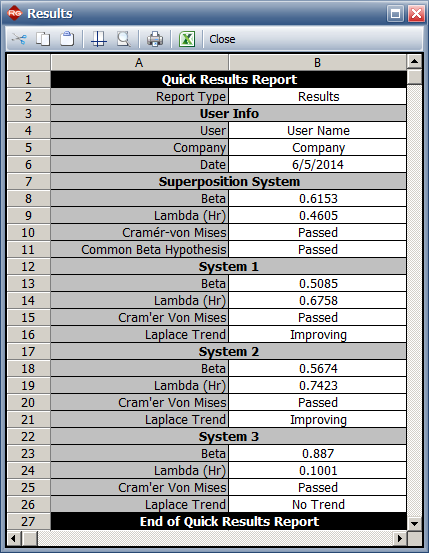
Beta = 0.615, Lambda = 0.461
Results in RGA
Since [math]\displaystyle{ \,\!S_{1}=S_{2}=S_{3}=0 }[/math] and [math]\displaystyle{ \,\!T_{1}=T_{2}=T_{3}=200 }[/math] then the maximum likelihood estimates of [math]\displaystyle{ \,\!\widehat{\beta} }[/math] and [math]\displaystyle{ \,\!\widehat{\lambda } }[/math] are given by:
- [math]\displaystyle{ \begin{align} \widehat{\beta }=&\frac{\sum_{q=1}^{K}N_{q}}{\sum_{q=1}^{K}\sum_{i=1}^{N_{q}}ln \left(\frac{T}{X_{iq}}\right)}\\ \\ =&0.6153 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \widehat{\lambda }=&\frac{\sum_{q=1}^{K}N_{q}}{KT^{\widehat{\beta }}}\\ \\ =&0.4605 \end{align}\,\! }[/math]