Test-Find-Test Data Reference Example
From ReliaWiki
Revision as of 15:50, 13 June 2014 by Beth Ann Paape (talk | contribs)
RGA_Reference_Examples_Banner.png
|
RGA_Reference_Examples |
This example compares the results for test-find-test data.
Reference Case
International Standard IEC 61164 (Reliability Growth in Product Design and Test – Statistical Test and Estimation Methods), Example 4, pg. 32.
Data
The following table shows the data.
| Failure Time | Classification Mode |
|---|---|
| 150 | BD1 |
| 253 | BD2 |
| 475 | BD3 |
| 540 | BD4 |
| 564 | BD5 |
| 636 | A |
| 722 | BD5 |
| 871 | A |
| 996 | BD6 |
| 1003 | BD7 |
| 1025 | A |
| 1120 | BD8 |
| 1209 | BD2 |
| 1255 | BD9 |
| 1334 | BD10 |
| 1647 | BD9 |
| 1774 | BD10 |
| 1927 | BD11 |
| 2130 | A |
| 2214 | A |
| 2293 | A |
| 2448 | A |
| 2490 | BD12 |
| 2508 | A |
| 2601 | BD1 |
| 2635 | BD8 |
| 2731 | A |
| 2747 | BD6 |
| 2850 | BD13 |
| 3040 | BD9 |
| 3154 | BD4 |
| 3171 | A |
| 3206 | A |
| 3245 | DB12 |
| 3249 | BD10 |
| 3420 | BD5 |
| 3502 | BD3 |
| 3646 | BD10 |
| 3649 | A |
| 3663 | BD2 |
| 3730 | BD8 |
| 3794 | BD14 |
| 3890 | BD15 |
| 3949 | A |
| 3952 | BD16 |
| BD Mode | EF |
|---|---|
| 1 | 0.7 |
| 2 | 0.7 |
| 3 | 0.8 |
| 4 | 0.8 |
| 5 | 0.9 |
| 6 | 0.9 |
| 7 | 0.5 |
| 8 | 0.8 |
| 9 | 0.9 |
| 10 | 0.7 |
| 11 | 0.7 |
| 12 | 0.6 |
| 13 | 0.6 |
| 14 | 0.7 |
| 15 | 0.7 |
| 16 | 0.5 |
Result
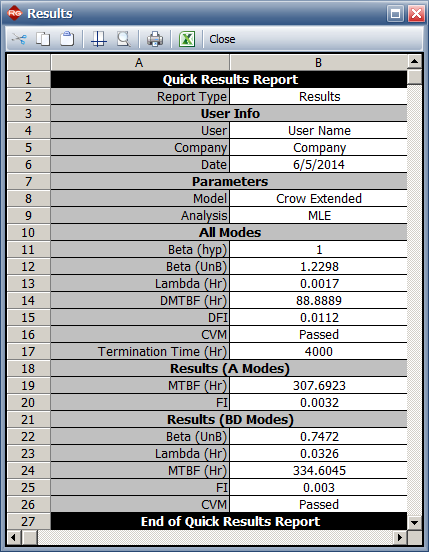
The book has the following results:
- BetaBD (UnB) = 0.7472, LambdaBD = 0.0326
- Unseen BD Mode Failure Intensity = 0.0030/hr
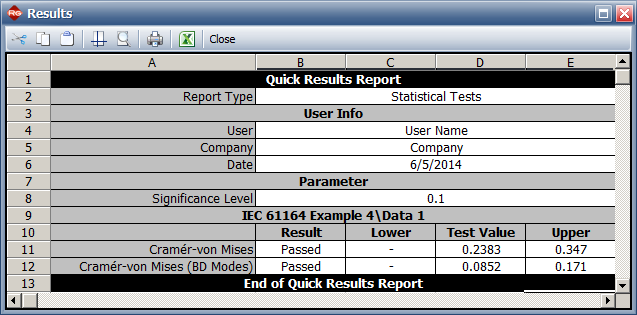
- Goodness of fit for BD modes: CVM = 0.085, critical value = 0.171 with significance level = 0.1. Since CVM < critical value can fail to reject hypothesis that the model fits the data.
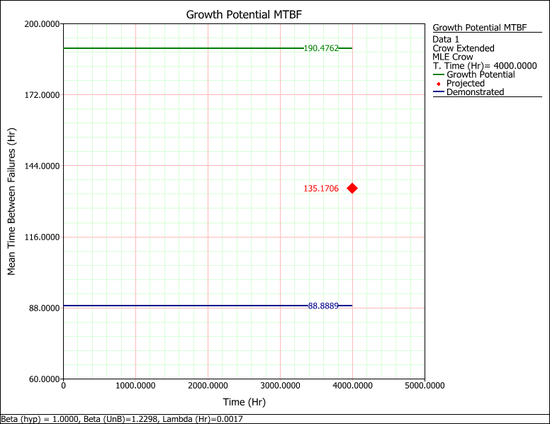
- DMTBF = 88.9 hours
- PMTBF = 135.1 hours
Results in RGA
Since test-find-test, the assumption is [math]\displaystyle{ \,\!\beta =1 }[/math]. Therefore:
- [math]\displaystyle{ \begin{align} DMTBF=&\frac{T}{N}\\ \\ =&\frac{4000}{45}\\ \\ =&88.8889 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \lambda _{p}=&\lambda _{A}+\sum_{i=1}^{N_{BD}}\left ( 1-d_{i} \right )\lambda _{i}+\bar{d}h\left ( T \right )\\ \\ =&\frac{N_{A}}{T}+\sum_{i=1}^{N_{BD}}\left ( 1-d_{i} \right )\frac{N_{i}}{T}+\bar{d}\lambda _{BD}\beta _{BD}T^{\beta -1}\\ \\ =&\frac{13}{4000}+0.002+\left ( 0.7188 \right )\left ( 0.032572 \right )\left ( 0.74715 \right )\left ( 4000 \right )^{0.7472-1}\\ \\ =&0.007398\\ \\ PMTBF=&\frac{1}{\lambda _{p}}\\ \\ =&135.17 \end{align}\,\! }[/math]