Test-Fix-Find-Test Data Example

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.

---

This example appears in the Reliability Growth and Repairable System Analysis Reference.

Consider the data given in the first table below. There were 56 total failures and [math]\displaystyle{ T=400\,\! }[/math]. The effectiveness factors of the unique BD modes are given in the second table. Determine the following:

1) Calculate the demonstrated MTBF and failure intensity.

2) Calculate the projected MTBF and failure intensity.

3) What is the rate at which unique BD modes are being generated during this test?

4) If the test continues for an additional 50 hours, what is the minimum number of new unique BD modes expected to be generated?

Test-Fix-Find-Test Data
[math]\displaystyle{ i\,\! }[/math]	[math]\displaystyle{ {{X}_{i}}\,\! }[/math]	Mode	[math]\displaystyle{ i\,\! }[/math]	[math]\displaystyle{ {{X}_{i}}\,\! }[/math]	Mode
1	0.7	BC17	29	192.7	BD11
2	3.7	BC17	30	213	A
3	13.2	BC17	31	244.8	A
4	15	BD1	32	249	BD12
5	17.6	BC18	33	250.8	A
6	25.3	BD2	34	260.1	BD1
7	47.5	BD3	35	263.5	BD8
8	54	BD4	36	273.1	A
9	54.5	BC19	37	274.7	BD6
10	56.4	BD5	38	282.8	BC27
11	63.6	A	39	285	BD13
12	72.2	BD5	40	304	BD9
13	99.2	BC20	41	315.4	BD4
14	99.6	BD6	42	317.1	A
15	100.3	BD7	43	320.6	A
16	102.5	A	44	324.5	BD12
17	112	BD8	45	324.9	BD10
18	112.2	BC21	46	342	BD5
19	120.9	BD2	47	350.2	BD3
20	121.9	BC22	48	355.2	BC28
21	125.5	BD9	49	364.6	BD10
22	133.4	BD10	50	364.9	A
23	151	BC23	51	366.3	BD2
24	163	BC24	52	373	BD8
25	164.7	BD9	53	379.4	BD14
26	174.5	BC25	54	389	BD15
27	177.4	BD10	55	394.9	A
28	191.6	BC26	56	395.2	BD16

Effectiveness Factors for the Unique BD Modes
BD Mode	EF [math]\displaystyle{ {{d}_{i}}\,\! }[/math]
1	.67
2	.72
3	.77
4	.77
5	.87
6	.92
7	.50
8	.85
9	.89
10	.74
11	.70
12	.63
13	.64
14	.72
15	.69
16	.46

Solution

1) In order to obtain [math]\displaystyle{ {{\widehat{\lambda }}_{CA}}\,\! }[/math], use the traditional Crow-AMSAA model for test-fix-test to fit all 56 data points, regardless of the failure mode classification to get:

[math]\displaystyle{ \begin{align} \widehat{\beta }= & 0.91026 \\ \widehat{\lambda }= & 0.23969 \end{align}\,\! }[/math]

Thus the achieved or demonstrated failure intensity is estimated by:

[math]\displaystyle{ \begin{align} {{\widehat{\lambda }}_{CA}} = & \widehat{\lambda }\widehat{\beta }{{T}^{\widehat{\beta }-1}} \\ = & 0.23969\times 0.91026\times {{400}^{(0.91026-1)}} \\ = & 0.12744 \end{align}\,\! }[/math]

The achieved or demonstrated MTBF, [math]\displaystyle{ {{M}_{CA}}\,\! }[/math], is the system reliability attained at the end of test, [math]\displaystyle{ T=400\,\! }[/math], and is estimated by:

[math]\displaystyle{ {{\widehat{M}}_{CA}}={{[{{\widehat{\lambda }}_{CA}}]}^{-1}}=7.84708\,\! }[/math]

2) For this data set, [math]\displaystyle{ M=16\,\! }[/math] and [math]\displaystyle{ T=400\,\! }[/math].

[math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=\frac{{{N}_{BD}}}{T}=\frac{32}{400}=0.08\,\! }[/math]

[math]\displaystyle{ \overline{d}=\underset{i=1}{\overset{M}{\mathop \sum }}\,{{d}_{i}}/M=0.72125\,\! }[/math]

[math]\displaystyle{ \underset{i=1}{\overset{16}{\mathop \sum }}\,(1-{{d}_{i}}){{N}_{i}}/T=0.01955\,\! }[/math]

Calculate maximum likelihood estimates, [math]\displaystyle{ \hat{\beta }\,\! }[/math] and [math]\displaystyle{ \hat{\lambda }\,\! }[/math], of the BD modes:

[math]\displaystyle{ \begin{align} {{{\hat{\beta }}}_{BD}}= & 0.74715 \\ {{{\hat{\lambda }}}_{BD}} = & 0.18197 \end{align}\,\! }[/math]

Then:

[math]\displaystyle{ \overline{d}\widehat{h}(T|BD)=0.0215\,\! }[/math]

Therefore:

[math]\displaystyle{ \begin{align} {{\widehat{\lambda }}_{EM}} = & {{\widehat{\lambda }}_{CA}}-{{\widehat{\lambda }}_{BD}}+\underset{i=1}{\overset{K}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T}+\overline{d}\widehat{h}(T|BD) \\ = & 0.12744-0.08+0.0196+0.0215 \\ = & 0.08854 \end{align}\,\! }[/math]

The Crow Extended model projected MTBF is:

[math]\displaystyle{ \begin{align} {{\widehat{M}}_{EM}} = & {{[{{\widehat{\lambda }}_{EM}}]}^{-1}} \\ = & 11.29418 \end{align}\,\! }[/math]

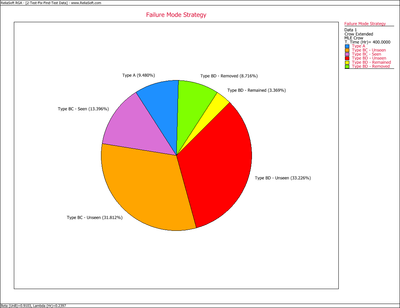
Consequently, based on the Crow Extended model and the data shown in the tables above, the MTBF grew to 7.85 as a result of the corrective actions for the BC failure modes during the test. The MTBF then jumped to 11.29 after the test as a result of the delayed corrective actions for the BD failure modes. The management strategy can be summarized by the Failure Mode Strategy plot, as shown next.

This pie chart shows that 9.48% of the system's failure intensity has been left in (A modes), 31.81% of the failure intensity due to the BC modes has not been seen yet and 13.40% was removed during the test (BC modes - seen). In addition, 33.23% of the failure intensity due to the BD modes has not been seen yet, 3.37% will remain in the system since the corrective actions will not be completely effective at eliminating the identified failure modes, and 8.72% will be removed after the delayed corrective actions.

3) The rate at which unique BD modes are being generated is equal to [math]\displaystyle{ h{{(T|BD)}^{-1}}\,\! }[/math], where:

[math]\displaystyle{ \begin{align} h{{(T|BD)}^{-1}} = & \frac{1}{{{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}}} \\ = & \frac{T}{M{{\widehat{\beta }}_{BD}}} \\ = & 33.4605 \end{align}\,\! }[/math]

4) Unique BD modes are being generated every 33.4605 hours. If the test continues for another 50 hours, then at least one new unique BD mode would be expected to be seen from this additional testing.

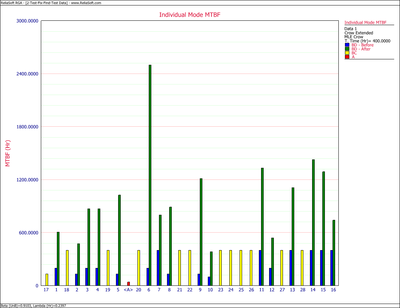
As shown in the next figure, the MTBF of each individual failure mode can be plotted, and the failure modes with the lowest MTBF can be identified. These are the failure modes that cause the majority of the system failures.