Crow Extended: Difference between revisions
Lisa Hacker (talk | contribs) No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
{{template:RGA BOOK|8|Crow Extended}} | {{template:RGA BOOK|8|Crow Extended}} | ||
{{rga crow extended}} | In a previous chapter, we discussed the most widely used traditional reliability growth tracking model, [[Crow-AMSAA - NHPP|Crow-AMSAA (NHPP)]]. Using this model for reliability growth analysis assumes that the corrective actions for the observed failure modes are incorporated during the test (test-fix-test). However, in actual practice, fixes may be delayed until after the completion of the test (test-find-test) or some fixes may be implemented during the test while others are delayed (test-fix-find-test). At the end of a test phase, two reliability estimates are of concern: demonstrated reliability and projected reliability. The demonstrated reliability, which is based on data generated during the test phase, is an estimate of the system reliability for its configuration at the end of the test phase. The projected reliability measures the impact of the delayed fixes at the end of the current test phase. | ||
<br> | |||
Most of the reliability growth literature has been concerned with procedures and models for calculating the demonstrated reliability and very little attention has been paid to techniques for reliability projections. The procedure for making reliability projections utilizes engineering assessments of the effectiveness of the delayed fixes for each observed failure mode. These effectiveness factors are then used with the data generated during the test phase to obtain a projected estimate for the updated configuration by adjusting the number of failures observed during the test phase. The process of estimating the projected reliability is accomplished using the Crow Extended model. The Crow Extended model allows for a flexible growth strategy that can include corrective actions performed during the test, as well as delayed corrective actions. The test-find-test and test-fix-find-test scenarios are simply subsets of the Crow Extended model. | |||
<br> | |||
<br> | |||
==Background== | |||
<br> | |||
When a system is tested and failure modes are observed, management can make one of two possible decisions, either to fix or not fix the failure mode. Therefore, the management strategy places failure modes into two categories: A modes and B modes. A modes are all failure modes such that when seen during the test no corrective action will be taken. This accounts for all modes for which management determines that it is not economically or otherwise justified to take a corrective action. In order to provide the assessment and management metric structure for corrective actions during and after a test, two types of B modes are defined. BC modes are corrected during the test and the corrective actions for BD modes are delayed until the end of the test. The management strategy is defined by how the corrective actions, if any, will be implemented. In summary, the classifications are defined as follows: | |||
<br> | |||
:• A indicates that no corrective action was performed or will be performed (management chooses not to address for technical, financial or other reasons). | |||
:• BC indicates that the corrective action was implemented during the test. The analysis assumes that the effect of the corrective action was experienced during the test (as with other test-fix-test reliability growth analyses). | |||
:• BD indicates that the corrective action will be delayed until after the completion of the current test. | |||
<br> | |||
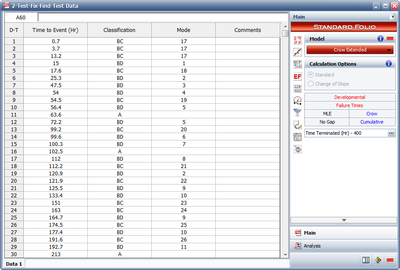
Figure CrowExtend1 shows an example of data entered for the Crow Extended model. | |||
As you can see, each failure is indicated with A, BC, or BD in the Classification column. In addition, any number or text can be used to specify the mode. In Figure CrowExtend1, numbers were used in the Mode column for simplicity, but you could just as easily use Seal Leak, or whatever designation you deem appropriate for identifying the failure mode. | |||
Reliability growth is achieved by decreasing the failure intensity. The failure intensity for the A failure modes will not change. Therefore, reliability growth can only be achieved by decreasing the BC and BD mode failure intensity. It is also clear that, in general, the only part of the BD mode failure intensity that can be decreased is that which has been seen during testing, since the failure intensity due to BD modes that were unseen during testing still remains. BC failure modes are corrected during test and the BC failure intensity will not change any more at the end of test. | |||
<br> | |||
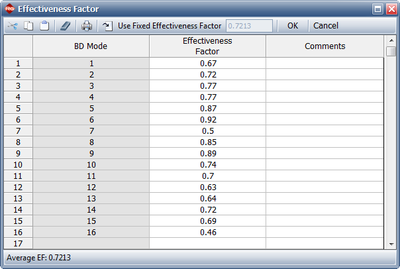
It is very important to note that once a BD failure mode is in the system it is rarely totally eliminated by a corrective action. After a BD mode has been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will generally remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective you will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made and must be a value between 0 and 1. A study on EFs showed that an average EF <math>d</math> was about 70 percent. Therefore, typically about 30 percent, i.e. 100 <math>(1-d)</math> percent, of the BD mode failure intensity will remain in the system after all of the corrective actions have been implemented. However, individual EFs for the failure modes may be larger or smaller than the average. Figure efffact1 displays RGA's Effectiveness Factor window where the effectiveness factors for each unique BD failure mode can be specified. | |||
[[Image:rga9.1.png|thumb|center|400px|Failure times data for a single system in cumulative format, including classification and mode information.]] | |||
<br> | |||
<br> | |||
[[Image:rga9.2.png|thumb|center|400px|Effectiveness factors defined for each unique BD mode.]] | |||
<br> | |||
{{test-find-test rga}} | |||
{{test-fix-find-test rga}} | |||
{{failure mode management strategy rga}} | |||
{{confidence bounds crow extended rga}} | |||
{{grouped data rga}} | |||
{{mixed data rga}} | |||
{{multiple systems with event codes rga}} | |||
==General Examples== | |||
===Example 8=== | |||
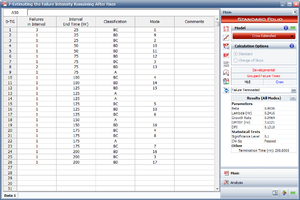
Three systems were subjected to a reliability growth test to evaluate the prototype of a new product. Once the test was completed a failure analysis was done and, based on this, a management strategy was able to be defined. It was determined that all corrective actions will be delayed until after the test. The collected data set is shown in Table 9.6 and the associated effectiveness factors for each unique BD mode are presented in Table 9.7. The prototype is required to meet a projected MTBF goal of 55 hours. Do the following: | |||
<br> | |||
<br> | |||
:1) Estimate the parameters of the Crow Extended model. | |||
:2) Based on the current management strategy what is the projected MTBF? | |||
:3) If the projected MTBF goal is not met, alter the current management strategy to meet this requirement with as little adjustment as possible and without changing the EFs of the existing BD modes. Assume an EF = 0.7 for any newly assigned BD modes. | |||
{|style= align="center" border="1" | |||
|- | |||
|colspan="4" style="text-align:center"|Table 9.6 - Multiple Systems (Concurrent Operating Times) data for Example 8 | |||
|- | |||
! | |||
!System 1 | |||
!System 2 | |||
!System 3 | |||
|- | |||
|Start Time||0|| 0|| 0 | |||
|- | |||
|End Time||541|| 454|| 436 | |||
|- | |||
|Times-to-Failure|| 83 BD37|| 26 BD25|| 23 BD30 | |||
|- | |||
| ||83 BD43|| 26 BD43|| 46 BD49 | |||
|- | |||
| ||83 BD46|| 57 BD37|| 127 BD47 | |||
|- | |||
| ||169 A45|| 64 BD19|| 166 A2 | |||
|- | |||
| ||213 A18|| 169 A45|| 169 BD23 | |||
|- | |||
| ||299 A42|| 213 A32|| 213 BD7 | |||
|- | |||
| ||375 A1|| 231 BD8|| 213 BD29 | |||
|- | |||
| ||431 BD16|| 231 BD25|| 255 BD26 | |||
|- | |||
| || ||231 BD27|| 369 A33 | |||
|- | |||
| || ||231 A28|| 374 BD29 | |||
|- | |||
| || ||304 BD24|| 380 BD22 | |||
|- | |||
| || ||383 BD40|| 415 BD7 | |||
|} | |||
<br> | |||
{|style= align="center" border="1" | |||
|- | |||
|colspan="2" style="text-align:center"|Table 9.7 - Effectiveness factors for Example 8 | |||
|- | |||
!BD Mode | |||
!Effectiveness Factor | |||
|- | |||
|30|| 0.75 | |||
|- | |||
|43|| 0.5 | |||
|- | |||
|25|| 0.5 | |||
|- | |||
|49|| 0.75 | |||
|- | |||
|37|| 0.9 | |||
|- | |||
|19|| 0.75 | |||
|- | |||
|46|| 0.75 | |||
|- | |||
|47|| 0.25 | |||
|- | |||
|23|| 0.5 | |||
|- | |||
|7|| 0.25 | |||
|- | |||
|29|| 0.25 | |||
|- | |||
|8|| 0.5 | |||
|- | |||
|27|| 0.5 | |||
|- | |||
|26|| 0.75 | |||
|- | |||
|24|| 0.5 | |||
|- | |||
|22|| 0.5 | |||
|- | |||
|40|| 0.75 | |||
|- | |||
|16|| 0.75 | |||
|} | |||
[[Image:rga9.29.png|thumb|center|300px|Entered data and the estimated Crow Extended parameters.]] | |||
<br> | |||
<br> | |||
[[Image:rga9.30.png|thumb|center|300px|Calculate the projected MTBF.]] | |||
<br> | |||
[[Image:rga9.31.png|thumb|center|300px|Individual Mode Failure Intensity chart.]] | |||
<br> | |||
[[Image:rga9.32.png|thumb|center|300px|Calculate the projected MTBF based on the change to the management strategy.]] | |||
<br> | |||
<br> | |||
====Solution to Example 8==== | |||
:1) Figure CrowExtend2 shows the estimated Crow Extended parameters. | |||
:2) There are a couple of ways to calculate the projected MTBF, but the easiest is via the Quick Calculation Pad (QCP), as shown in Figure CrowExtend3. | |||
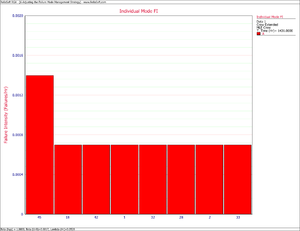
:3) From the previous question, the projected MTBF is estimated to be 53.9390 hours, which is below the goal of 55 hours. To reach our goal, or to see if we can even get there, the management strategy must be changed. The effectiveness factors for the existing BD modes cannot be changed, however it is possible to change an A mode to a BD mode. But which A mode(s) should be changed? To answer this question, you can view the Individual Mode Failure Intensity plot with just the A modes displayed as shown in Figure CrowExtend4. As you can see from the plot, failure mode A45 has the highest failure intensity. Therefore, among the A modes this particular failure mode is having the greatest negative effect in regards to the system MTBF. So change A45 to BD45. Be sure to change all instances of A45 to a BD mode. Enter an effectiveness factor for BD45 equal to 0.7 and recalculate the parameters of the Crow Extended model. Now go back to the QCP to calculate the projected MTBF as shown in Figure CrowExtend5. The projected MTBF is now estimated to be 55.5903 hours. Based on the change in the management strategy, the projected MTBF goal is now expected to be met. | |||
<br> | |||
<br> | |||
===Example 9=== | |||
<br> | |||
A reliability growth test was conducted for 200 hours. Some of the corrective actions were applied during the test while others were delayed until after the test was completed. The data set is given in Table 9.8. The effectiveness factors for the BD modes are given in Table 9.9. Do the following: | |||
<br> | |||
<br> | |||
:1) Estimate the parameters of the Crow Extended model. | |||
:2) Determine the average effectiveness factor of the BC modes using the Function Wizard. | |||
:3) What percent of the failure intensity will be left in the system due to the BD modes after implementing the delayed fixes? | |||
<br> | |||
{|style= align="center" border="1" | |||
|- | |||
|colspan="4" style="text-align:center"|Table 9.8 - Grouped Failure Times data for Example 9 | |||
|- | |||
!Number at Event | |||
!Time to Event | |||
!Classification | |||
!Mode | |||
|- | |||
|3|| 25|| BC|| 1 | |||
|- | |||
|1|| 25|| BD|| 9 | |||
|- | |||
|1|| 25|| BC|| 2 | |||
|- | |||
|1|| 50|| BD|| 10 | |||
|- | |||
|1|| 50|| BD|| 11 | |||
|- | |||
|1|| 75|| BD|| 12 | |||
|- | |||
|1|| 75|| BC|| 3 | |||
|- | |||
|2|| 75|| BD|| 13 | |||
|- | |||
|1|| 75|| A|| | |||
|- | |||
|1|| 100|| BC|| 4 | |||
|- | |||
|1|| 100|| BD|| 14 | |||
|- | |||
|1|| 125|| BD|| 15 | |||
|- | |||
|1|| 125|| A|| | |||
|- | |||
|1|| 125|| A|| | |||
|- | |||
|1|| 125|| BC|| 5 | |||
|- | |||
|1|| 125|| BD|| 10 | |||
|- | |||
|1|| 125|| BC|| 6 | |||
|- | |||
|1|| 150|| A|| | |||
|- | |||
|1|| 150|| BD|| 16 | |||
|- | |||
|1|| 175|| BC|| 4 | |||
|- | |||
|1|| 175|| BC|| 8 | |||
|- | |||
|1|| 175|| A|| | |||
|- | |||
|1|| 175|| BC|| 7 | |||
|- | |||
|1|| 200|| BD|| 16 | |||
|- | |||
|1|| 200|| BC|| 3 | |||
|- | |||
|1|| 200|| BD|| 17 | |||
|} | |||
{|style= align="center" border="1" | |||
|- | |||
|colspan="2" style="text-align:center"|Table 9.9 - Effectiveness factors for Example 9 | |||
|- | |||
!BD Mode | |||
!Effectiveness Factor | |||
|- | |||
|9|| 0.75 | |||
|- | |||
|10|| 0.5 | |||
|- | |||
|11|| 0.9 | |||
|- | |||
|12|| 0.6 | |||
|- | |||
|13|| 0.8 | |||
|- | |||
|14|| 0.8 | |||
|- | |||
|15|| 0.25 | |||
|- | |||
|16|| 0.75 | |||
|- | |||
|17|| 0.8 | |||
|} | |||
====Solution to Example 9==== | |||
:1) Figure CrowExtend6 shows the estimated parameters of the Crow Extended model. | |||
:2) After inserting a General Spreadsheet into the Folio, the Function Wizard can be accessed via the Tools menu. Once the Function Wizard is loaded, select Average Effectiveness Factor from the list of available functions and under Avg. Eff. Factor select BC modes as shown in Figure CrowExtend7. Click OK and the result will be placed into the General Spreadsheet. The average effectiveness factor for the BC modes is 0.6983. | |||
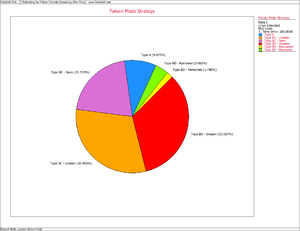
:3) The percent of the failure intensity left in the system due to the BD modes can be determined using the Failure Mode Strategy plot as shown in Figure CrowExtend8. Therefore, the percent of the failure intensity left in the system due to the BD modes is 1.79%. | |||
[[Image:rga9.33.png|thumb|center|300px|Entered data and the estimated Crow Extended parameters.]] | |||
[[Image:rga9.34.png|thumb|center|300px|Calculate the average effectiveness factor for the BC modes using the Function Wizard.]] | |||
[[Image:rga9.35.png|thumb|center|300px|Failure Mode Strategy plot.]] | |||
<br> | |||
===Example 10=== | |||
<br> | |||
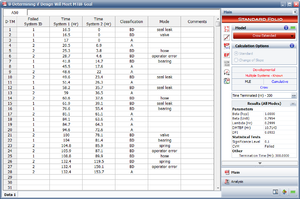
Two prototypes of a new design are tested simultaneously. Whenever a failure was observed for one unit, the current operating time of the other unit was also recorded. The test was terminated after 300 hours. All of the design changes for the prototypes were delayed until after completing the test and the data set is given in Table 9.10. Assume a fixed effectiveness factor equal to 0.7. The MTBF goal for the new design is 30 hours. Do the following: | |||
<br> | |||
<br> | |||
:1) Estimate the parameters of the Crow Extended model. | |||
:2) What is the projected MTBF and growth potential? | |||
:3) Under the current management strategy, is it even possible to reach the MTBF goal of 30 hours? | |||
<br> | |||
{|style= align="center" border="1" | |||
|- | |||
|colspan="5" style="text-align:center"|Table 9.10 - Multiple Systems (Known Operating Times) data for Example 10 | |||
|- | |||
!Failed Unit ID | |||
!Time Unit 1 | |||
!Time Unit 2 | |||
!Classification | |||
!Mode | |||
|- | |||
|1|| 16.5|| 0|| BD|| seal leak | |||
|- | |||
|1|| 16.5|| 0|| BD|| valve | |||
|- | |||
|1|| 17|| 0|| A|| | |||
|- | |||
|2|| 20.5|| 0.9|| A|| | |||
|- | |||
|2|| 25.3|| 3.8|| BD|| hose | |||
|- | |||
|2|| 28.7|| 4.6|| BD|| operator error | |||
|- | |||
|1|| 41.8|| 14.7|| BD|| bearing | |||
|- | |||
|1|| 45.5|| 17.6|| A|| | |||
|- | |||
|2|| 48.6|| 22|| A|| | |||
|- | |||
|2|| 49.6|| 23.4|| BD|| seal leak | |||
|- | |||
|1|| 51.4|| 26.3|| A|| | |||
|- | |||
|1|| 58.2|| 35.7|| BD|| seal leak | |||
|- | |||
|2|| 59|| 36.5|| A|| | |||
|- | |||
|2|| 60.6|| 37.6|| BD|| hose | |||
|- | |||
|1|| 61.9|| 39.1|| BD|| seal leak | |||
|- | |||
|1|| 76.6|| 55.4|| BD|| bearing | |||
|- | |||
|2|| 81.1|| 61.1|| A|| | |||
|- | |||
|1|| 84.1|| 63.6|| A|| | |||
|- | |||
|1|| 84.7|| 64.3|| A|| | |||
|- | |||
|1|| 94.6|| 72.6|| A|| | |||
|- | |||
|2|| 100|| 78.1|| BD|| valve | |||
|- | |||
|1|| 104|| 81.4|| BD|| bearing | |||
|- | |||
|2|| 104.8|| 85.9|| BD|| spring | |||
|- | |||
|2|| 105.9|| 87.1|| BD|| operator error | |||
|- | |||
|1|| 108.8|| 89.9|| BD|| hose | |||
|- | |||
|2|| 132.4|| 119.5|| BD|| spring | |||
|- | |||
|2|| 132.4|| 150.1|| BD|| operator error | |||
|- | |||
|2|| 132.4|| 153.7|| A|| | |||
|} | |||
<br> | |||
====Solution to Example 10==== | |||
<br> | |||
:1) Figure CrowExtend9 shows the estimated Crow Extended parameters. | |||
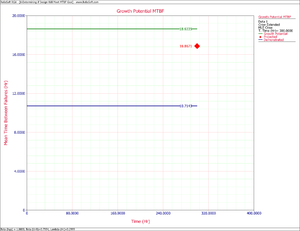
:2) One possible method to calculate the projected MTBF and growth potential is to use the Quick Calculation Pad, but you can also view these two values at the same time by viewing the Growth Potential MTBF plot, which is displayed in Figure CrowExtend10. From the plot, the projected MTBF is equal to 16.87 hours and the growth potential is equal to 18.63 hours. | |||
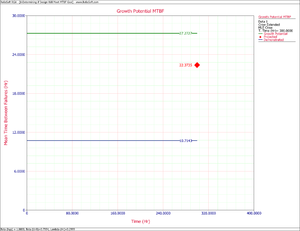
:3) The current projected MTBF and growth potential MTBF are both well below the required goal of 30 hours. To check if this goal can even be reached, you can set the effectiveness factor equal to 1. In other words, if all of the corrective actions were to remove the failure modes completely then what would be the projected and growth potential MTBF? After changing the fixed effectiveness factor to 1, the parameters are recalculated and the Growth Potential plot is refreshed. The refreshed plot is shown in Figure CrowExtend11. Even if you assume an effectiveness factor equal to 1, the growth potential is still only 27.27 hours. Based on the current design process, it will not be possible to reach the MTBF goal of 30 hours. Therefore, there are basically two options: start a new design stage or reduce the required MTBF goal. | |||
<math></math> | |||
[[Image:rga9.36.png|thumb|center|300px|Entered data and the estimated Crow Extended parameters.]] | |||
<br> | |||
<math></math> | |||
[[Image:rga9.37.png|thumb|center|300px|Growth Potential MTBF plot (EF=0.7)]] | |||
<br> | |||
<br> | |||
[[Image:rga9.38.png|thumb|center|300px|Growth Potential MTBF plot (EF=1)]] | |||
<br> | |||
Revision as of 01:11, 23 August 2012
In a previous chapter, we discussed the most widely used traditional reliability growth tracking model, Crow-AMSAA (NHPP). Using this model for reliability growth analysis assumes that the corrective actions for the observed failure modes are incorporated during the test (test-fix-test). However, in actual practice, fixes may be delayed until after the completion of the test (test-find-test) or some fixes may be implemented during the test while others are delayed (test-fix-find-test). At the end of a test phase, two reliability estimates are of concern: demonstrated reliability and projected reliability. The demonstrated reliability, which is based on data generated during the test phase, is an estimate of the system reliability for its configuration at the end of the test phase. The projected reliability measures the impact of the delayed fixes at the end of the current test phase.
Most of the reliability growth literature has been concerned with procedures and models for calculating the demonstrated reliability and very little attention has been paid to techniques for reliability projections. The procedure for making reliability projections utilizes engineering assessments of the effectiveness of the delayed fixes for each observed failure mode. These effectiveness factors are then used with the data generated during the test phase to obtain a projected estimate for the updated configuration by adjusting the number of failures observed during the test phase. The process of estimating the projected reliability is accomplished using the Crow Extended model. The Crow Extended model allows for a flexible growth strategy that can include corrective actions performed during the test, as well as delayed corrective actions. The test-find-test and test-fix-find-test scenarios are simply subsets of the Crow Extended model.
Background
When a system is tested and failure modes are observed, management can make one of two possible decisions, either to fix or not fix the failure mode. Therefore, the management strategy places failure modes into two categories: A modes and B modes. A modes are all failure modes such that when seen during the test no corrective action will be taken. This accounts for all modes for which management determines that it is not economically or otherwise justified to take a corrective action. In order to provide the assessment and management metric structure for corrective actions during and after a test, two types of B modes are defined. BC modes are corrected during the test and the corrective actions for BD modes are delayed until the end of the test. The management strategy is defined by how the corrective actions, if any, will be implemented. In summary, the classifications are defined as follows:
- • A indicates that no corrective action was performed or will be performed (management chooses not to address for technical, financial or other reasons).
- • BC indicates that the corrective action was implemented during the test. The analysis assumes that the effect of the corrective action was experienced during the test (as with other test-fix-test reliability growth analyses).
- • BD indicates that the corrective action will be delayed until after the completion of the current test.
Figure CrowExtend1 shows an example of data entered for the Crow Extended model.
As you can see, each failure is indicated with A, BC, or BD in the Classification column. In addition, any number or text can be used to specify the mode. In Figure CrowExtend1, numbers were used in the Mode column for simplicity, but you could just as easily use Seal Leak, or whatever designation you deem appropriate for identifying the failure mode.
Reliability growth is achieved by decreasing the failure intensity. The failure intensity for the A failure modes will not change. Therefore, reliability growth can only be achieved by decreasing the BC and BD mode failure intensity. It is also clear that, in general, the only part of the BD mode failure intensity that can be decreased is that which has been seen during testing, since the failure intensity due to BD modes that were unseen during testing still remains. BC failure modes are corrected during test and the BC failure intensity will not change any more at the end of test.
It is very important to note that once a BD failure mode is in the system it is rarely totally eliminated by a corrective action. After a BD mode has been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will generally remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective you will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made and must be a value between 0 and 1. A study on EFs showed that an average EF [math]\displaystyle{ d }[/math] was about 70 percent. Therefore, typically about 30 percent, i.e. 100 [math]\displaystyle{ (1-d) }[/math] percent, of the BD mode failure intensity will remain in the system after all of the corrective actions have been implemented. However, individual EFs for the failure modes may be larger or smaller than the average. Figure efffact1 displays RGA's Effectiveness Factor window where the effectiveness factors for each unique BD failure mode can be specified.
In a previous chapter, we discussed the most widely used traditional reliability growth tracking model, Crow-AMSAA (NHPP). Using this model for reliability growth analysis assumes that the corrective actions for the observed failure modes are incorporated during the test (test-fix-test). However, in actual practice, fixes may be delayed until after the completion of the test (test-find-test) or some fixes may be implemented during the test while others are delayed (test-fix-find-test). At the end of a test phase, two reliability estimates are of concern: demonstrated reliability and projected reliability. The demonstrated reliability, which is based on data generated during the test phase, is an estimate of the system reliability for its configuration at the end of the test phase. The projected reliability measures the impact of the delayed fixes at the end of the current test phase.
Most of the reliability growth literature has been concerned with procedures and models for calculating the demonstrated reliability and very little attention has been paid to techniques for reliability projections. The procedure for making reliability projections utilizes engineering assessments of the effectiveness of the delayed fixes for each observed failure mode. These effectiveness factors are then used with the data generated during the test phase to obtain a projected estimate for the updated configuration by adjusting the number of failures observed during the test phase. The process of estimating the projected reliability is accomplished using the Crow Extended model. The Crow Extended model allows for a flexible growth strategy that can include corrective actions performed during the test, as well as delayed corrective actions. The test-find-test and test-fix-find-test scenarios are simply subsets of the Crow Extended model.
Background
When a system is tested and failure modes are observed, management can make one of two possible decisions, either to fix or not fix the failure mode. Therefore, the management strategy places failure modes into two categories: A modes and B modes. A modes are all failure modes such that when seen during the test no corrective action will be taken. This accounts for all modes for which management determines that it is not economically or otherwise justified to take a corrective action. In order to provide the assessment and management metric structure for corrective actions during and after a test, two types of B modes are defined. BC modes are corrected during the test and the corrective actions for BD modes are delayed until the end of the test. The management strategy is defined by how the corrective actions, if any, will be implemented. In summary, the classifications are defined as follows:
- • A indicates that no corrective action was performed or will be performed (management chooses not to address for technical, financial or other reasons).
- • BC indicates that the corrective action was implemented during the test. The analysis assumes that the effect of the corrective action was experienced during the test (as with other test-fix-test reliability growth analyses).
- • BD indicates that the corrective action will be delayed until after the completion of the current test.
Figure CrowExtend1 shows an example of data entered for the Crow Extended model.
As you can see, each failure is indicated with A, BC, or BD in the Classification column. In addition, any number or text can be used to specify the mode. In Figure CrowExtend1, numbers were used in the Mode column for simplicity, but you could just as easily use Seal Leak, or whatever designation you deem appropriate for identifying the failure mode.
Reliability growth is achieved by decreasing the failure intensity. The failure intensity for the A failure modes will not change. Therefore, reliability growth can only be achieved by decreasing the BC and BD mode failure intensity. It is also clear that, in general, the only part of the BD mode failure intensity that can be decreased is that which has been seen during testing, since the failure intensity due to BD modes that were unseen during testing still remains. BC failure modes are corrected during test and the BC failure intensity will not change any more at the end of test.
It is very important to note that once a BD failure mode is in the system it is rarely totally eliminated by a corrective action. After a BD mode has been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will generally remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective you will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made and must be a value between 0 and 1. A study on EFs showed that an average EF [math]\displaystyle{ d }[/math] was about 70 percent. Therefore, typically about 30 percent, i.e. 100 [math]\displaystyle{ (1-d) }[/math] percent, of the BD mode failure intensity will remain in the system after all of the corrective actions have been implemented. However, individual EFs for the failure modes may be larger or smaller than the average. Figure efffact1 displays RGA's Effectiveness Factor window where the effectiveness factors for each unique BD failure mode can be specified.
Template loop detected: Template:Test-find-test rga
Template loop detected: Template:Test-fix-find-test rga
Template loop detected: Template:Failure mode management strategy rga
Template loop detected: Template:Confidence bounds crow extended rga
Template loop detected: Template:Grouped data rga
Template loop detected: Template:Mixed data rga
Template loop detected: Template:Multiple systems with event codes rga
General Examples
Example 8
Three systems were subjected to a reliability growth test to evaluate the prototype of a new product. Once the test was completed a failure analysis was done and, based on this, a management strategy was able to be defined. It was determined that all corrective actions will be delayed until after the test. The collected data set is shown in Table 9.6 and the associated effectiveness factors for each unique BD mode are presented in Table 9.7. The prototype is required to meet a projected MTBF goal of 55 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Based on the current management strategy what is the projected MTBF?
- 3) If the projected MTBF goal is not met, alter the current management strategy to meet this requirement with as little adjustment as possible and without changing the EFs of the existing BD modes. Assume an EF = 0.7 for any newly assigned BD modes.
| Table 9.6 - Multiple Systems (Concurrent Operating Times) data for Example 8 | |||
| System 1 | System 2 | System 3 | |
|---|---|---|---|
| Start Time | 0 | 0 | 0 |
| End Time | 541 | 454 | 436 |
| Times-to-Failure | 83 BD37 | 26 BD25 | 23 BD30 |
| 83 BD43 | 26 BD43 | 46 BD49 | |
| 83 BD46 | 57 BD37 | 127 BD47 | |
| 169 A45 | 64 BD19 | 166 A2 | |
| 213 A18 | 169 A45 | 169 BD23 | |
| 299 A42 | 213 A32 | 213 BD7 | |
| 375 A1 | 231 BD8 | 213 BD29 | |
| 431 BD16 | 231 BD25 | 255 BD26 | |
| 231 BD27 | 369 A33 | ||
| 231 A28 | 374 BD29 | ||
| 304 BD24 | 380 BD22 | ||
| 383 BD40 | 415 BD7 | ||
| Table 9.7 - Effectiveness factors for Example 8 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 30 | 0.75 |
| 43 | 0.5 |
| 25 | 0.5 |
| 49 | 0.75 |
| 37 | 0.9 |
| 19 | 0.75 |
| 46 | 0.75 |
| 47 | 0.25 |
| 23 | 0.5 |
| 7 | 0.25 |
| 29 | 0.25 |
| 8 | 0.5 |
| 27 | 0.5 |
| 26 | 0.75 |
| 24 | 0.5 |
| 22 | 0.5 |
| 40 | 0.75 |
| 16 | 0.75 |
Solution to Example 8
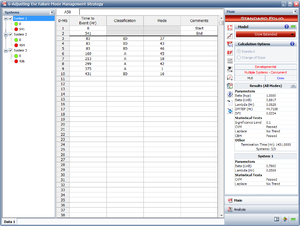
- 1) Figure CrowExtend2 shows the estimated Crow Extended parameters.
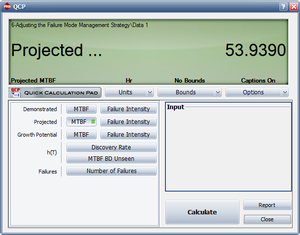
- 2) There are a couple of ways to calculate the projected MTBF, but the easiest is via the Quick Calculation Pad (QCP), as shown in Figure CrowExtend3.
- 3) From the previous question, the projected MTBF is estimated to be 53.9390 hours, which is below the goal of 55 hours. To reach our goal, or to see if we can even get there, the management strategy must be changed. The effectiveness factors for the existing BD modes cannot be changed, however it is possible to change an A mode to a BD mode. But which A mode(s) should be changed? To answer this question, you can view the Individual Mode Failure Intensity plot with just the A modes displayed as shown in Figure CrowExtend4. As you can see from the plot, failure mode A45 has the highest failure intensity. Therefore, among the A modes this particular failure mode is having the greatest negative effect in regards to the system MTBF. So change A45 to BD45. Be sure to change all instances of A45 to a BD mode. Enter an effectiveness factor for BD45 equal to 0.7 and recalculate the parameters of the Crow Extended model. Now go back to the QCP to calculate the projected MTBF as shown in Figure CrowExtend5. The projected MTBF is now estimated to be 55.5903 hours. Based on the change in the management strategy, the projected MTBF goal is now expected to be met.
Example 9
A reliability growth test was conducted for 200 hours. Some of the corrective actions were applied during the test while others were delayed until after the test was completed. The data set is given in Table 9.8. The effectiveness factors for the BD modes are given in Table 9.9. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Determine the average effectiveness factor of the BC modes using the Function Wizard.
- 3) What percent of the failure intensity will be left in the system due to the BD modes after implementing the delayed fixes?
| Table 9.8 - Grouped Failure Times data for Example 9 | |||
| Number at Event | Time to Event | Classification | Mode |
|---|---|---|---|
| 3 | 25 | BC | 1 |
| 1 | 25 | BD | 9 |
| 1 | 25 | BC | 2 |
| 1 | 50 | BD | 10 |
| 1 | 50 | BD | 11 |
| 1 | 75 | BD | 12 |
| 1 | 75 | BC | 3 |
| 2 | 75 | BD | 13 |
| 1 | 75 | A | |
| 1 | 100 | BC | 4 |
| 1 | 100 | BD | 14 |
| 1 | 125 | BD | 15 |
| 1 | 125 | A | |
| 1 | 125 | A | |
| 1 | 125 | BC | 5 |
| 1 | 125 | BD | 10 |
| 1 | 125 | BC | 6 |
| 1 | 150 | A | |
| 1 | 150 | BD | 16 |
| 1 | 175 | BC | 4 |
| 1 | 175 | BC | 8 |
| 1 | 175 | A | |
| 1 | 175 | BC | 7 |
| 1 | 200 | BD | 16 |
| 1 | 200 | BC | 3 |
| 1 | 200 | BD | 17 |
| Table 9.9 - Effectiveness factors for Example 9 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 9 | 0.75 |
| 10 | 0.5 |
| 11 | 0.9 |
| 12 | 0.6 |
| 13 | 0.8 |
| 14 | 0.8 |
| 15 | 0.25 |
| 16 | 0.75 |
| 17 | 0.8 |
Solution to Example 9
- 1) Figure CrowExtend6 shows the estimated parameters of the Crow Extended model.
- 2) After inserting a General Spreadsheet into the Folio, the Function Wizard can be accessed via the Tools menu. Once the Function Wizard is loaded, select Average Effectiveness Factor from the list of available functions and under Avg. Eff. Factor select BC modes as shown in Figure CrowExtend7. Click OK and the result will be placed into the General Spreadsheet. The average effectiveness factor for the BC modes is 0.6983.
- 3) The percent of the failure intensity left in the system due to the BD modes can be determined using the Failure Mode Strategy plot as shown in Figure CrowExtend8. Therefore, the percent of the failure intensity left in the system due to the BD modes is 1.79%.
Example 10
Two prototypes of a new design are tested simultaneously. Whenever a failure was observed for one unit, the current operating time of the other unit was also recorded. The test was terminated after 300 hours. All of the design changes for the prototypes were delayed until after completing the test and the data set is given in Table 9.10. Assume a fixed effectiveness factor equal to 0.7. The MTBF goal for the new design is 30 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) What is the projected MTBF and growth potential?
- 3) Under the current management strategy, is it even possible to reach the MTBF goal of 30 hours?
| Table 9.10 - Multiple Systems (Known Operating Times) data for Example 10 | ||||
| Failed Unit ID | Time Unit 1 | Time Unit 2 | Classification | Mode |
|---|---|---|---|---|
| 1 | 16.5 | 0 | BD | seal leak |
| 1 | 16.5 | 0 | BD | valve |
| 1 | 17 | 0 | A | |
| 2 | 20.5 | 0.9 | A | |
| 2 | 25.3 | 3.8 | BD | hose |
| 2 | 28.7 | 4.6 | BD | operator error |
| 1 | 41.8 | 14.7 | BD | bearing |
| 1 | 45.5 | 17.6 | A | |
| 2 | 48.6 | 22 | A | |
| 2 | 49.6 | 23.4 | BD | seal leak |
| 1 | 51.4 | 26.3 | A | |
| 1 | 58.2 | 35.7 | BD | seal leak |
| 2 | 59 | 36.5 | A | |
| 2 | 60.6 | 37.6 | BD | hose |
| 1 | 61.9 | 39.1 | BD | seal leak |
| 1 | 76.6 | 55.4 | BD | bearing |
| 2 | 81.1 | 61.1 | A | |
| 1 | 84.1 | 63.6 | A | |
| 1 | 84.7 | 64.3 | A | |
| 1 | 94.6 | 72.6 | A | |
| 2 | 100 | 78.1 | BD | valve |
| 1 | 104 | 81.4 | BD | bearing |
| 2 | 104.8 | 85.9 | BD | spring |
| 2 | 105.9 | 87.1 | BD | operator error |
| 1 | 108.8 | 89.9 | BD | hose |
| 2 | 132.4 | 119.5 | BD | spring |
| 2 | 132.4 | 150.1 | BD | operator error |
| 2 | 132.4 | 153.7 | A | |
Solution to Example 10
- 1) Figure CrowExtend9 shows the estimated Crow Extended parameters.
- 2) One possible method to calculate the projected MTBF and growth potential is to use the Quick Calculation Pad, but you can also view these two values at the same time by viewing the Growth Potential MTBF plot, which is displayed in Figure CrowExtend10. From the plot, the projected MTBF is equal to 16.87 hours and the growth potential is equal to 18.63 hours.
- 3) The current projected MTBF and growth potential MTBF are both well below the required goal of 30 hours. To check if this goal can even be reached, you can set the effectiveness factor equal to 1. In other words, if all of the corrective actions were to remove the failure modes completely then what would be the projected and growth potential MTBF? After changing the fixed effectiveness factor to 1, the parameters are recalculated and the Growth Potential plot is refreshed. The refreshed plot is shown in Figure CrowExtend11. Even if you assume an effectiveness factor equal to 1, the growth potential is still only 27.27 hours. Based on the current design process, it will not be possible to reach the MTBF goal of 30 hours. Therefore, there are basically two options: start a new design stage or reduce the required MTBF goal.
[math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math]
In a previous chapter, we discussed the most widely used traditional reliability growth tracking model, Crow-AMSAA (NHPP). Using this model for reliability growth analysis assumes that the corrective actions for the observed failure modes are incorporated during the test (test-fix-test). However, in actual practice, fixes may be delayed until after the completion of the test (test-find-test) or some fixes may be implemented during the test while others are delayed (test-fix-find-test). At the end of a test phase, two reliability estimates are of concern: demonstrated reliability and projected reliability. The demonstrated reliability, which is based on data generated during the test phase, is an estimate of the system reliability for its configuration at the end of the test phase. The projected reliability measures the impact of the delayed fixes at the end of the current test phase.
Most of the reliability growth literature has been concerned with procedures and models for calculating the demonstrated reliability and very little attention has been paid to techniques for reliability projections. The procedure for making reliability projections utilizes engineering assessments of the effectiveness of the delayed fixes for each observed failure mode. These effectiveness factors are then used with the data generated during the test phase to obtain a projected estimate for the updated configuration by adjusting the number of failures observed during the test phase. The process of estimating the projected reliability is accomplished using the Crow Extended model. The Crow Extended model allows for a flexible growth strategy that can include corrective actions performed during the test, as well as delayed corrective actions. The test-find-test and test-fix-find-test scenarios are simply subsets of the Crow Extended model.
Background
When a system is tested and failure modes are observed, management can make one of two possible decisions, either to fix or not fix the failure mode. Therefore, the management strategy places failure modes into two categories: A modes and B modes. A modes are all failure modes such that when seen during the test no corrective action will be taken. This accounts for all modes for which management determines that it is not economically or otherwise justified to take a corrective action. In order to provide the assessment and management metric structure for corrective actions during and after a test, two types of B modes are defined. BC modes are corrected during the test and the corrective actions for BD modes are delayed until the end of the test. The management strategy is defined by how the corrective actions, if any, will be implemented. In summary, the classifications are defined as follows:
- • A indicates that no corrective action was performed or will be performed (management chooses not to address for technical, financial or other reasons).
- • BC indicates that the corrective action was implemented during the test. The analysis assumes that the effect of the corrective action was experienced during the test (as with other test-fix-test reliability growth analyses).
- • BD indicates that the corrective action will be delayed until after the completion of the current test.
Figure CrowExtend1 shows an example of data entered for the Crow Extended model.
As you can see, each failure is indicated with A, BC, or BD in the Classification column. In addition, any number or text can be used to specify the mode. In Figure CrowExtend1, numbers were used in the Mode column for simplicity, but you could just as easily use Seal Leak, or whatever designation you deem appropriate for identifying the failure mode.
Reliability growth is achieved by decreasing the failure intensity. The failure intensity for the A failure modes will not change. Therefore, reliability growth can only be achieved by decreasing the BC and BD mode failure intensity. It is also clear that, in general, the only part of the BD mode failure intensity that can be decreased is that which has been seen during testing, since the failure intensity due to BD modes that were unseen during testing still remains. BC failure modes are corrected during test and the BC failure intensity will not change any more at the end of test.
It is very important to note that once a BD failure mode is in the system it is rarely totally eliminated by a corrective action. After a BD mode has been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will generally remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective you will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made and must be a value between 0 and 1. A study on EFs showed that an average EF [math]\displaystyle{ d }[/math] was about 70 percent. Therefore, typically about 30 percent, i.e. 100 [math]\displaystyle{ (1-d) }[/math] percent, of the BD mode failure intensity will remain in the system after all of the corrective actions have been implemented. However, individual EFs for the failure modes may be larger or smaller than the average. Figure efffact1 displays RGA's Effectiveness Factor window where the effectiveness factors for each unique BD failure mode can be specified.
Template loop detected: Template:Test-find-test rga
Template loop detected: Template:Test-fix-find-test rga
Template loop detected: Template:Failure mode management strategy rga
Template loop detected: Template:Confidence bounds crow extended rga
Template loop detected: Template:Grouped data rga
Template loop detected: Template:Mixed data rga
Template loop detected: Template:Multiple systems with event codes rga
General Examples
Example 8
Three systems were subjected to a reliability growth test to evaluate the prototype of a new product. Once the test was completed a failure analysis was done and, based on this, a management strategy was able to be defined. It was determined that all corrective actions will be delayed until after the test. The collected data set is shown in Table 9.6 and the associated effectiveness factors for each unique BD mode are presented in Table 9.7. The prototype is required to meet a projected MTBF goal of 55 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Based on the current management strategy what is the projected MTBF?
- 3) If the projected MTBF goal is not met, alter the current management strategy to meet this requirement with as little adjustment as possible and without changing the EFs of the existing BD modes. Assume an EF = 0.7 for any newly assigned BD modes.
| Table 9.6 - Multiple Systems (Concurrent Operating Times) data for Example 8 | |||
| System 1 | System 2 | System 3 | |
|---|---|---|---|
| Start Time | 0 | 0 | 0 |
| End Time | 541 | 454 | 436 |
| Times-to-Failure | 83 BD37 | 26 BD25 | 23 BD30 |
| 83 BD43 | 26 BD43 | 46 BD49 | |
| 83 BD46 | 57 BD37 | 127 BD47 | |
| 169 A45 | 64 BD19 | 166 A2 | |
| 213 A18 | 169 A45 | 169 BD23 | |
| 299 A42 | 213 A32 | 213 BD7 | |
| 375 A1 | 231 BD8 | 213 BD29 | |
| 431 BD16 | 231 BD25 | 255 BD26 | |
| 231 BD27 | 369 A33 | ||
| 231 A28 | 374 BD29 | ||
| 304 BD24 | 380 BD22 | ||
| 383 BD40 | 415 BD7 | ||
| Table 9.7 - Effectiveness factors for Example 8 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 30 | 0.75 |
| 43 | 0.5 |
| 25 | 0.5 |
| 49 | 0.75 |
| 37 | 0.9 |
| 19 | 0.75 |
| 46 | 0.75 |
| 47 | 0.25 |
| 23 | 0.5 |
| 7 | 0.25 |
| 29 | 0.25 |
| 8 | 0.5 |
| 27 | 0.5 |
| 26 | 0.75 |
| 24 | 0.5 |
| 22 | 0.5 |
| 40 | 0.75 |
| 16 | 0.75 |
Solution to Example 8
- 1) Figure CrowExtend2 shows the estimated Crow Extended parameters.
- 2) There are a couple of ways to calculate the projected MTBF, but the easiest is via the Quick Calculation Pad (QCP), as shown in Figure CrowExtend3.
- 3) From the previous question, the projected MTBF is estimated to be 53.9390 hours, which is below the goal of 55 hours. To reach our goal, or to see if we can even get there, the management strategy must be changed. The effectiveness factors for the existing BD modes cannot be changed, however it is possible to change an A mode to a BD mode. But which A mode(s) should be changed? To answer this question, you can view the Individual Mode Failure Intensity plot with just the A modes displayed as shown in Figure CrowExtend4. As you can see from the plot, failure mode A45 has the highest failure intensity. Therefore, among the A modes this particular failure mode is having the greatest negative effect in regards to the system MTBF. So change A45 to BD45. Be sure to change all instances of A45 to a BD mode. Enter an effectiveness factor for BD45 equal to 0.7 and recalculate the parameters of the Crow Extended model. Now go back to the QCP to calculate the projected MTBF as shown in Figure CrowExtend5. The projected MTBF is now estimated to be 55.5903 hours. Based on the change in the management strategy, the projected MTBF goal is now expected to be met.
Example 9
A reliability growth test was conducted for 200 hours. Some of the corrective actions were applied during the test while others were delayed until after the test was completed. The data set is given in Table 9.8. The effectiveness factors for the BD modes are given in Table 9.9. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Determine the average effectiveness factor of the BC modes using the Function Wizard.
- 3) What percent of the failure intensity will be left in the system due to the BD modes after implementing the delayed fixes?
| Table 9.8 - Grouped Failure Times data for Example 9 | |||
| Number at Event | Time to Event | Classification | Mode |
|---|---|---|---|
| 3 | 25 | BC | 1 |
| 1 | 25 | BD | 9 |
| 1 | 25 | BC | 2 |
| 1 | 50 | BD | 10 |
| 1 | 50 | BD | 11 |
| 1 | 75 | BD | 12 |
| 1 | 75 | BC | 3 |
| 2 | 75 | BD | 13 |
| 1 | 75 | A | |
| 1 | 100 | BC | 4 |
| 1 | 100 | BD | 14 |
| 1 | 125 | BD | 15 |
| 1 | 125 | A | |
| 1 | 125 | A | |
| 1 | 125 | BC | 5 |
| 1 | 125 | BD | 10 |
| 1 | 125 | BC | 6 |
| 1 | 150 | A | |
| 1 | 150 | BD | 16 |
| 1 | 175 | BC | 4 |
| 1 | 175 | BC | 8 |
| 1 | 175 | A | |
| 1 | 175 | BC | 7 |
| 1 | 200 | BD | 16 |
| 1 | 200 | BC | 3 |
| 1 | 200 | BD | 17 |
| Table 9.9 - Effectiveness factors for Example 9 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 9 | 0.75 |
| 10 | 0.5 |
| 11 | 0.9 |
| 12 | 0.6 |
| 13 | 0.8 |
| 14 | 0.8 |
| 15 | 0.25 |
| 16 | 0.75 |
| 17 | 0.8 |
Solution to Example 9
- 1) Figure CrowExtend6 shows the estimated parameters of the Crow Extended model.
- 2) After inserting a General Spreadsheet into the Folio, the Function Wizard can be accessed via the Tools menu. Once the Function Wizard is loaded, select Average Effectiveness Factor from the list of available functions and under Avg. Eff. Factor select BC modes as shown in Figure CrowExtend7. Click OK and the result will be placed into the General Spreadsheet. The average effectiveness factor for the BC modes is 0.6983.
- 3) The percent of the failure intensity left in the system due to the BD modes can be determined using the Failure Mode Strategy plot as shown in Figure CrowExtend8. Therefore, the percent of the failure intensity left in the system due to the BD modes is 1.79%.
Example 10
Two prototypes of a new design are tested simultaneously. Whenever a failure was observed for one unit, the current operating time of the other unit was also recorded. The test was terminated after 300 hours. All of the design changes for the prototypes were delayed until after completing the test and the data set is given in Table 9.10. Assume a fixed effectiveness factor equal to 0.7. The MTBF goal for the new design is 30 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) What is the projected MTBF and growth potential?
- 3) Under the current management strategy, is it even possible to reach the MTBF goal of 30 hours?
| Table 9.10 - Multiple Systems (Known Operating Times) data for Example 10 | ||||
| Failed Unit ID | Time Unit 1 | Time Unit 2 | Classification | Mode |
|---|---|---|---|---|
| 1 | 16.5 | 0 | BD | seal leak |
| 1 | 16.5 | 0 | BD | valve |
| 1 | 17 | 0 | A | |
| 2 | 20.5 | 0.9 | A | |
| 2 | 25.3 | 3.8 | BD | hose |
| 2 | 28.7 | 4.6 | BD | operator error |
| 1 | 41.8 | 14.7 | BD | bearing |
| 1 | 45.5 | 17.6 | A | |
| 2 | 48.6 | 22 | A | |
| 2 | 49.6 | 23.4 | BD | seal leak |
| 1 | 51.4 | 26.3 | A | |
| 1 | 58.2 | 35.7 | BD | seal leak |
| 2 | 59 | 36.5 | A | |
| 2 | 60.6 | 37.6 | BD | hose |
| 1 | 61.9 | 39.1 | BD | seal leak |
| 1 | 76.6 | 55.4 | BD | bearing |
| 2 | 81.1 | 61.1 | A | |
| 1 | 84.1 | 63.6 | A | |
| 1 | 84.7 | 64.3 | A | |
| 1 | 94.6 | 72.6 | A | |
| 2 | 100 | 78.1 | BD | valve |
| 1 | 104 | 81.4 | BD | bearing |
| 2 | 104.8 | 85.9 | BD | spring |
| 2 | 105.9 | 87.1 | BD | operator error |
| 1 | 108.8 | 89.9 | BD | hose |
| 2 | 132.4 | 119.5 | BD | spring |
| 2 | 132.4 | 150.1 | BD | operator error |
| 2 | 132.4 | 153.7 | A | |
Solution to Example 10
- 1) Figure CrowExtend9 shows the estimated Crow Extended parameters.
- 2) One possible method to calculate the projected MTBF and growth potential is to use the Quick Calculation Pad, but you can also view these two values at the same time by viewing the Growth Potential MTBF plot, which is displayed in Figure CrowExtend10. From the plot, the projected MTBF is equal to 16.87 hours and the growth potential is equal to 18.63 hours.
- 3) The current projected MTBF and growth potential MTBF are both well below the required goal of 30 hours. To check if this goal can even be reached, you can set the effectiveness factor equal to 1. In other words, if all of the corrective actions were to remove the failure modes completely then what would be the projected and growth potential MTBF? After changing the fixed effectiveness factor to 1, the parameters are recalculated and the Growth Potential plot is refreshed. The refreshed plot is shown in Figure CrowExtend11. Even if you assume an effectiveness factor equal to 1, the growth potential is still only 27.27 hours. Based on the current design process, it will not be possible to reach the MTBF goal of 30 hours. Therefore, there are basically two options: start a new design stage or reduce the required MTBF goal.
[math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math]
In a previous chapter, we discussed the most widely used traditional reliability growth tracking model, Crow-AMSAA (NHPP). Using this model for reliability growth analysis assumes that the corrective actions for the observed failure modes are incorporated during the test (test-fix-test). However, in actual practice, fixes may be delayed until after the completion of the test (test-find-test) or some fixes may be implemented during the test while others are delayed (test-fix-find-test). At the end of a test phase, two reliability estimates are of concern: demonstrated reliability and projected reliability. The demonstrated reliability, which is based on data generated during the test phase, is an estimate of the system reliability for its configuration at the end of the test phase. The projected reliability measures the impact of the delayed fixes at the end of the current test phase.
Most of the reliability growth literature has been concerned with procedures and models for calculating the demonstrated reliability and very little attention has been paid to techniques for reliability projections. The procedure for making reliability projections utilizes engineering assessments of the effectiveness of the delayed fixes for each observed failure mode. These effectiveness factors are then used with the data generated during the test phase to obtain a projected estimate for the updated configuration by adjusting the number of failures observed during the test phase. The process of estimating the projected reliability is accomplished using the Crow Extended model. The Crow Extended model allows for a flexible growth strategy that can include corrective actions performed during the test, as well as delayed corrective actions. The test-find-test and test-fix-find-test scenarios are simply subsets of the Crow Extended model.
Background
When a system is tested and failure modes are observed, management can make one of two possible decisions, either to fix or not fix the failure mode. Therefore, the management strategy places failure modes into two categories: A modes and B modes. A modes are all failure modes such that when seen during the test no corrective action will be taken. This accounts for all modes for which management determines that it is not economically or otherwise justified to take a corrective action. In order to provide the assessment and management metric structure for corrective actions during and after a test, two types of B modes are defined. BC modes are corrected during the test and the corrective actions for BD modes are delayed until the end of the test. The management strategy is defined by how the corrective actions, if any, will be implemented. In summary, the classifications are defined as follows:
- • A indicates that no corrective action was performed or will be performed (management chooses not to address for technical, financial or other reasons).
- • BC indicates that the corrective action was implemented during the test. The analysis assumes that the effect of the corrective action was experienced during the test (as with other test-fix-test reliability growth analyses).
- • BD indicates that the corrective action will be delayed until after the completion of the current test.
Figure CrowExtend1 shows an example of data entered for the Crow Extended model.
As you can see, each failure is indicated with A, BC, or BD in the Classification column. In addition, any number or text can be used to specify the mode. In Figure CrowExtend1, numbers were used in the Mode column for simplicity, but you could just as easily use Seal Leak, or whatever designation you deem appropriate for identifying the failure mode.
Reliability growth is achieved by decreasing the failure intensity. The failure intensity for the A failure modes will not change. Therefore, reliability growth can only be achieved by decreasing the BC and BD mode failure intensity. It is also clear that, in general, the only part of the BD mode failure intensity that can be decreased is that which has been seen during testing, since the failure intensity due to BD modes that were unseen during testing still remains. BC failure modes are corrected during test and the BC failure intensity will not change any more at the end of test.
It is very important to note that once a BD failure mode is in the system it is rarely totally eliminated by a corrective action. After a BD mode has been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will generally remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective you will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made and must be a value between 0 and 1. A study on EFs showed that an average EF [math]\displaystyle{ d }[/math] was about 70 percent. Therefore, typically about 30 percent, i.e. 100 [math]\displaystyle{ (1-d) }[/math] percent, of the BD mode failure intensity will remain in the system after all of the corrective actions have been implemented. However, individual EFs for the failure modes may be larger or smaller than the average. Figure efffact1 displays RGA's Effectiveness Factor window where the effectiveness factors for each unique BD failure mode can be specified.
Template loop detected: Template:Test-find-test rga
Template loop detected: Template:Test-fix-find-test rga
Template loop detected: Template:Failure mode management strategy rga
Template loop detected: Template:Confidence bounds crow extended rga
Template loop detected: Template:Grouped data rga
Template loop detected: Template:Mixed data rga
Template loop detected: Template:Multiple systems with event codes rga
General Examples
Example 8
Three systems were subjected to a reliability growth test to evaluate the prototype of a new product. Once the test was completed a failure analysis was done and, based on this, a management strategy was able to be defined. It was determined that all corrective actions will be delayed until after the test. The collected data set is shown in Table 9.6 and the associated effectiveness factors for each unique BD mode are presented in Table 9.7. The prototype is required to meet a projected MTBF goal of 55 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Based on the current management strategy what is the projected MTBF?
- 3) If the projected MTBF goal is not met, alter the current management strategy to meet this requirement with as little adjustment as possible and without changing the EFs of the existing BD modes. Assume an EF = 0.7 for any newly assigned BD modes.
| Table 9.6 - Multiple Systems (Concurrent Operating Times) data for Example 8 | |||
| System 1 | System 2 | System 3 | |
|---|---|---|---|
| Start Time | 0 | 0 | 0 |
| End Time | 541 | 454 | 436 |
| Times-to-Failure | 83 BD37 | 26 BD25 | 23 BD30 |
| 83 BD43 | 26 BD43 | 46 BD49 | |
| 83 BD46 | 57 BD37 | 127 BD47 | |
| 169 A45 | 64 BD19 | 166 A2 | |
| 213 A18 | 169 A45 | 169 BD23 | |
| 299 A42 | 213 A32 | 213 BD7 | |
| 375 A1 | 231 BD8 | 213 BD29 | |
| 431 BD16 | 231 BD25 | 255 BD26 | |
| 231 BD27 | 369 A33 | ||
| 231 A28 | 374 BD29 | ||
| 304 BD24 | 380 BD22 | ||
| 383 BD40 | 415 BD7 | ||
| Table 9.7 - Effectiveness factors for Example 8 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 30 | 0.75 |
| 43 | 0.5 |
| 25 | 0.5 |
| 49 | 0.75 |
| 37 | 0.9 |
| 19 | 0.75 |
| 46 | 0.75 |
| 47 | 0.25 |
| 23 | 0.5 |
| 7 | 0.25 |
| 29 | 0.25 |
| 8 | 0.5 |
| 27 | 0.5 |
| 26 | 0.75 |
| 24 | 0.5 |
| 22 | 0.5 |
| 40 | 0.75 |
| 16 | 0.75 |
Solution to Example 8
- 1) Figure CrowExtend2 shows the estimated Crow Extended parameters.
- 2) There are a couple of ways to calculate the projected MTBF, but the easiest is via the Quick Calculation Pad (QCP), as shown in Figure CrowExtend3.
- 3) From the previous question, the projected MTBF is estimated to be 53.9390 hours, which is below the goal of 55 hours. To reach our goal, or to see if we can even get there, the management strategy must be changed. The effectiveness factors for the existing BD modes cannot be changed, however it is possible to change an A mode to a BD mode. But which A mode(s) should be changed? To answer this question, you can view the Individual Mode Failure Intensity plot with just the A modes displayed as shown in Figure CrowExtend4. As you can see from the plot, failure mode A45 has the highest failure intensity. Therefore, among the A modes this particular failure mode is having the greatest negative effect in regards to the system MTBF. So change A45 to BD45. Be sure to change all instances of A45 to a BD mode. Enter an effectiveness factor for BD45 equal to 0.7 and recalculate the parameters of the Crow Extended model. Now go back to the QCP to calculate the projected MTBF as shown in Figure CrowExtend5. The projected MTBF is now estimated to be 55.5903 hours. Based on the change in the management strategy, the projected MTBF goal is now expected to be met.
Example 9
A reliability growth test was conducted for 200 hours. Some of the corrective actions were applied during the test while others were delayed until after the test was completed. The data set is given in Table 9.8. The effectiveness factors for the BD modes are given in Table 9.9. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Determine the average effectiveness factor of the BC modes using the Function Wizard.
- 3) What percent of the failure intensity will be left in the system due to the BD modes after implementing the delayed fixes?
| Table 9.8 - Grouped Failure Times data for Example 9 | |||
| Number at Event | Time to Event | Classification | Mode |
|---|---|---|---|
| 3 | 25 | BC | 1 |
| 1 | 25 | BD | 9 |
| 1 | 25 | BC | 2 |
| 1 | 50 | BD | 10 |
| 1 | 50 | BD | 11 |
| 1 | 75 | BD | 12 |
| 1 | 75 | BC | 3 |
| 2 | 75 | BD | 13 |
| 1 | 75 | A | |
| 1 | 100 | BC | 4 |
| 1 | 100 | BD | 14 |
| 1 | 125 | BD | 15 |
| 1 | 125 | A | |
| 1 | 125 | A | |
| 1 | 125 | BC | 5 |
| 1 | 125 | BD | 10 |
| 1 | 125 | BC | 6 |
| 1 | 150 | A | |
| 1 | 150 | BD | 16 |
| 1 | 175 | BC | 4 |
| 1 | 175 | BC | 8 |
| 1 | 175 | A | |
| 1 | 175 | BC | 7 |
| 1 | 200 | BD | 16 |
| 1 | 200 | BC | 3 |
| 1 | 200 | BD | 17 |
| Table 9.9 - Effectiveness factors for Example 9 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 9 | 0.75 |
| 10 | 0.5 |
| 11 | 0.9 |
| 12 | 0.6 |
| 13 | 0.8 |
| 14 | 0.8 |
| 15 | 0.25 |
| 16 | 0.75 |
| 17 | 0.8 |
Solution to Example 9
- 1) Figure CrowExtend6 shows the estimated parameters of the Crow Extended model.
- 2) After inserting a General Spreadsheet into the Folio, the Function Wizard can be accessed via the Tools menu. Once the Function Wizard is loaded, select Average Effectiveness Factor from the list of available functions and under Avg. Eff. Factor select BC modes as shown in Figure CrowExtend7. Click OK and the result will be placed into the General Spreadsheet. The average effectiveness factor for the BC modes is 0.6983.
- 3) The percent of the failure intensity left in the system due to the BD modes can be determined using the Failure Mode Strategy plot as shown in Figure CrowExtend8. Therefore, the percent of the failure intensity left in the system due to the BD modes is 1.79%.
Example 10
Two prototypes of a new design are tested simultaneously. Whenever a failure was observed for one unit, the current operating time of the other unit was also recorded. The test was terminated after 300 hours. All of the design changes for the prototypes were delayed until after completing the test and the data set is given in Table 9.10. Assume a fixed effectiveness factor equal to 0.7. The MTBF goal for the new design is 30 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) What is the projected MTBF and growth potential?
- 3) Under the current management strategy, is it even possible to reach the MTBF goal of 30 hours?
| Table 9.10 - Multiple Systems (Known Operating Times) data for Example 10 | ||||
| Failed Unit ID | Time Unit 1 | Time Unit 2 | Classification | Mode |
|---|---|---|---|---|
| 1 | 16.5 | 0 | BD | seal leak |
| 1 | 16.5 | 0 | BD | valve |
| 1 | 17 | 0 | A | |
| 2 | 20.5 | 0.9 | A | |
| 2 | 25.3 | 3.8 | BD | hose |
| 2 | 28.7 | 4.6 | BD | operator error |
| 1 | 41.8 | 14.7 | BD | bearing |
| 1 | 45.5 | 17.6 | A | |
| 2 | 48.6 | 22 | A | |
| 2 | 49.6 | 23.4 | BD | seal leak |
| 1 | 51.4 | 26.3 | A | |
| 1 | 58.2 | 35.7 | BD | seal leak |
| 2 | 59 | 36.5 | A | |
| 2 | 60.6 | 37.6 | BD | hose |
| 1 | 61.9 | 39.1 | BD | seal leak |
| 1 | 76.6 | 55.4 | BD | bearing |
| 2 | 81.1 | 61.1 | A | |
| 1 | 84.1 | 63.6 | A | |
| 1 | 84.7 | 64.3 | A | |
| 1 | 94.6 | 72.6 | A | |
| 2 | 100 | 78.1 | BD | valve |
| 1 | 104 | 81.4 | BD | bearing |
| 2 | 104.8 | 85.9 | BD | spring |
| 2 | 105.9 | 87.1 | BD | operator error |
| 1 | 108.8 | 89.9 | BD | hose |
| 2 | 132.4 | 119.5 | BD | spring |
| 2 | 132.4 | 150.1 | BD | operator error |
| 2 | 132.4 | 153.7 | A | |
Solution to Example 10
- 1) Figure CrowExtend9 shows the estimated Crow Extended parameters.
- 2) One possible method to calculate the projected MTBF and growth potential is to use the Quick Calculation Pad, but you can also view these two values at the same time by viewing the Growth Potential MTBF plot, which is displayed in Figure CrowExtend10. From the plot, the projected MTBF is equal to 16.87 hours and the growth potential is equal to 18.63 hours.
- 3) The current projected MTBF and growth potential MTBF are both well below the required goal of 30 hours. To check if this goal can even be reached, you can set the effectiveness factor equal to 1. In other words, if all of the corrective actions were to remove the failure modes completely then what would be the projected and growth potential MTBF? After changing the fixed effectiveness factor to 1, the parameters are recalculated and the Growth Potential plot is refreshed. The refreshed plot is shown in Figure CrowExtend11. Even if you assume an effectiveness factor equal to 1, the growth potential is still only 27.27 hours. Based on the current design process, it will not be possible to reach the MTBF goal of 30 hours. Therefore, there are basically two options: start a new design stage or reduce the required MTBF goal.
[math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math]
In a previous chapter, we discussed the most widely used traditional reliability growth tracking model, Crow-AMSAA (NHPP). Using this model for reliability growth analysis assumes that the corrective actions for the observed failure modes are incorporated during the test (test-fix-test). However, in actual practice, fixes may be delayed until after the completion of the test (test-find-test) or some fixes may be implemented during the test while others are delayed (test-fix-find-test). At the end of a test phase, two reliability estimates are of concern: demonstrated reliability and projected reliability. The demonstrated reliability, which is based on data generated during the test phase, is an estimate of the system reliability for its configuration at the end of the test phase. The projected reliability measures the impact of the delayed fixes at the end of the current test phase.
Most of the reliability growth literature has been concerned with procedures and models for calculating the demonstrated reliability and very little attention has been paid to techniques for reliability projections. The procedure for making reliability projections utilizes engineering assessments of the effectiveness of the delayed fixes for each observed failure mode. These effectiveness factors are then used with the data generated during the test phase to obtain a projected estimate for the updated configuration by adjusting the number of failures observed during the test phase. The process of estimating the projected reliability is accomplished using the Crow Extended model. The Crow Extended model allows for a flexible growth strategy that can include corrective actions performed during the test, as well as delayed corrective actions. The test-find-test and test-fix-find-test scenarios are simply subsets of the Crow Extended model.
Background
When a system is tested and failure modes are observed, management can make one of two possible decisions, either to fix or not fix the failure mode. Therefore, the management strategy places failure modes into two categories: A modes and B modes. A modes are all failure modes such that when seen during the test no corrective action will be taken. This accounts for all modes for which management determines that it is not economically or otherwise justified to take a corrective action. In order to provide the assessment and management metric structure for corrective actions during and after a test, two types of B modes are defined. BC modes are corrected during the test and the corrective actions for BD modes are delayed until the end of the test. The management strategy is defined by how the corrective actions, if any, will be implemented. In summary, the classifications are defined as follows:
- • A indicates that no corrective action was performed or will be performed (management chooses not to address for technical, financial or other reasons).
- • BC indicates that the corrective action was implemented during the test. The analysis assumes that the effect of the corrective action was experienced during the test (as with other test-fix-test reliability growth analyses).
- • BD indicates that the corrective action will be delayed until after the completion of the current test.
Figure CrowExtend1 shows an example of data entered for the Crow Extended model.
As you can see, each failure is indicated with A, BC, or BD in the Classification column. In addition, any number or text can be used to specify the mode. In Figure CrowExtend1, numbers were used in the Mode column for simplicity, but you could just as easily use Seal Leak, or whatever designation you deem appropriate for identifying the failure mode.
Reliability growth is achieved by decreasing the failure intensity. The failure intensity for the A failure modes will not change. Therefore, reliability growth can only be achieved by decreasing the BC and BD mode failure intensity. It is also clear that, in general, the only part of the BD mode failure intensity that can be decreased is that which has been seen during testing, since the failure intensity due to BD modes that were unseen during testing still remains. BC failure modes are corrected during test and the BC failure intensity will not change any more at the end of test.
It is very important to note that once a BD failure mode is in the system it is rarely totally eliminated by a corrective action. After a BD mode has been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will generally remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective you will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made and must be a value between 0 and 1. A study on EFs showed that an average EF [math]\displaystyle{ d }[/math] was about 70 percent. Therefore, typically about 30 percent, i.e. 100 [math]\displaystyle{ (1-d) }[/math] percent, of the BD mode failure intensity will remain in the system after all of the corrective actions have been implemented. However, individual EFs for the failure modes may be larger or smaller than the average. Figure efffact1 displays RGA's Effectiveness Factor window where the effectiveness factors for each unique BD failure mode can be specified.
Template loop detected: Template:Test-find-test rga
Template loop detected: Template:Test-fix-find-test rga
Template loop detected: Template:Failure mode management strategy rga
Template loop detected: Template:Confidence bounds crow extended rga
Template loop detected: Template:Grouped data rga
Template loop detected: Template:Mixed data rga
Template loop detected: Template:Multiple systems with event codes rga
General Examples
Example 8
Three systems were subjected to a reliability growth test to evaluate the prototype of a new product. Once the test was completed a failure analysis was done and, based on this, a management strategy was able to be defined. It was determined that all corrective actions will be delayed until after the test. The collected data set is shown in Table 9.6 and the associated effectiveness factors for each unique BD mode are presented in Table 9.7. The prototype is required to meet a projected MTBF goal of 55 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Based on the current management strategy what is the projected MTBF?
- 3) If the projected MTBF goal is not met, alter the current management strategy to meet this requirement with as little adjustment as possible and without changing the EFs of the existing BD modes. Assume an EF = 0.7 for any newly assigned BD modes.
| Table 9.6 - Multiple Systems (Concurrent Operating Times) data for Example 8 | |||
| System 1 | System 2 | System 3 | |
|---|---|---|---|
| Start Time | 0 | 0 | 0 |
| End Time | 541 | 454 | 436 |
| Times-to-Failure | 83 BD37 | 26 BD25 | 23 BD30 |
| 83 BD43 | 26 BD43 | 46 BD49 | |
| 83 BD46 | 57 BD37 | 127 BD47 | |
| 169 A45 | 64 BD19 | 166 A2 | |
| 213 A18 | 169 A45 | 169 BD23 | |
| 299 A42 | 213 A32 | 213 BD7 | |
| 375 A1 | 231 BD8 | 213 BD29 | |
| 431 BD16 | 231 BD25 | 255 BD26 | |
| 231 BD27 | 369 A33 | ||
| 231 A28 | 374 BD29 | ||
| 304 BD24 | 380 BD22 | ||
| 383 BD40 | 415 BD7 | ||
| Table 9.7 - Effectiveness factors for Example 8 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 30 | 0.75 |
| 43 | 0.5 |
| 25 | 0.5 |
| 49 | 0.75 |
| 37 | 0.9 |
| 19 | 0.75 |
| 46 | 0.75 |
| 47 | 0.25 |
| 23 | 0.5 |
| 7 | 0.25 |
| 29 | 0.25 |
| 8 | 0.5 |
| 27 | 0.5 |
| 26 | 0.75 |
| 24 | 0.5 |
| 22 | 0.5 |
| 40 | 0.75 |
| 16 | 0.75 |
Solution to Example 8
- 1) Figure CrowExtend2 shows the estimated Crow Extended parameters.
- 2) There are a couple of ways to calculate the projected MTBF, but the easiest is via the Quick Calculation Pad (QCP), as shown in Figure CrowExtend3.
- 3) From the previous question, the projected MTBF is estimated to be 53.9390 hours, which is below the goal of 55 hours. To reach our goal, or to see if we can even get there, the management strategy must be changed. The effectiveness factors for the existing BD modes cannot be changed, however it is possible to change an A mode to a BD mode. But which A mode(s) should be changed? To answer this question, you can view the Individual Mode Failure Intensity plot with just the A modes displayed as shown in Figure CrowExtend4. As you can see from the plot, failure mode A45 has the highest failure intensity. Therefore, among the A modes this particular failure mode is having the greatest negative effect in regards to the system MTBF. So change A45 to BD45. Be sure to change all instances of A45 to a BD mode. Enter an effectiveness factor for BD45 equal to 0.7 and recalculate the parameters of the Crow Extended model. Now go back to the QCP to calculate the projected MTBF as shown in Figure CrowExtend5. The projected MTBF is now estimated to be 55.5903 hours. Based on the change in the management strategy, the projected MTBF goal is now expected to be met.
Example 9
A reliability growth test was conducted for 200 hours. Some of the corrective actions were applied during the test while others were delayed until after the test was completed. The data set is given in Table 9.8. The effectiveness factors for the BD modes are given in Table 9.9. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Determine the average effectiveness factor of the BC modes using the Function Wizard.
- 3) What percent of the failure intensity will be left in the system due to the BD modes after implementing the delayed fixes?
| Table 9.8 - Grouped Failure Times data for Example 9 | |||
| Number at Event | Time to Event | Classification | Mode |
|---|---|---|---|
| 3 | 25 | BC | 1 |
| 1 | 25 | BD | 9 |
| 1 | 25 | BC | 2 |
| 1 | 50 | BD | 10 |
| 1 | 50 | BD | 11 |
| 1 | 75 | BD | 12 |
| 1 | 75 | BC | 3 |
| 2 | 75 | BD | 13 |
| 1 | 75 | A | |
| 1 | 100 | BC | 4 |
| 1 | 100 | BD | 14 |
| 1 | 125 | BD | 15 |
| 1 | 125 | A | |
| 1 | 125 | A | |
| 1 | 125 | BC | 5 |
| 1 | 125 | BD | 10 |
| 1 | 125 | BC | 6 |
| 1 | 150 | A | |
| 1 | 150 | BD | 16 |
| 1 | 175 | BC | 4 |
| 1 | 175 | BC | 8 |
| 1 | 175 | A | |
| 1 | 175 | BC | 7 |
| 1 | 200 | BD | 16 |
| 1 | 200 | BC | 3 |
| 1 | 200 | BD | 17 |
| Table 9.9 - Effectiveness factors for Example 9 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 9 | 0.75 |
| 10 | 0.5 |
| 11 | 0.9 |
| 12 | 0.6 |
| 13 | 0.8 |
| 14 | 0.8 |
| 15 | 0.25 |
| 16 | 0.75 |
| 17 | 0.8 |
Solution to Example 9
- 1) Figure CrowExtend6 shows the estimated parameters of the Crow Extended model.
- 2) After inserting a General Spreadsheet into the Folio, the Function Wizard can be accessed via the Tools menu. Once the Function Wizard is loaded, select Average Effectiveness Factor from the list of available functions and under Avg. Eff. Factor select BC modes as shown in Figure CrowExtend7. Click OK and the result will be placed into the General Spreadsheet. The average effectiveness factor for the BC modes is 0.6983.
- 3) The percent of the failure intensity left in the system due to the BD modes can be determined using the Failure Mode Strategy plot as shown in Figure CrowExtend8. Therefore, the percent of the failure intensity left in the system due to the BD modes is 1.79%.
Example 10
Two prototypes of a new design are tested simultaneously. Whenever a failure was observed for one unit, the current operating time of the other unit was also recorded. The test was terminated after 300 hours. All of the design changes for the prototypes were delayed until after completing the test and the data set is given in Table 9.10. Assume a fixed effectiveness factor equal to 0.7. The MTBF goal for the new design is 30 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) What is the projected MTBF and growth potential?
- 3) Under the current management strategy, is it even possible to reach the MTBF goal of 30 hours?
| Table 9.10 - Multiple Systems (Known Operating Times) data for Example 10 | ||||
| Failed Unit ID | Time Unit 1 | Time Unit 2 | Classification | Mode |
|---|---|---|---|---|
| 1 | 16.5 | 0 | BD | seal leak |
| 1 | 16.5 | 0 | BD | valve |
| 1 | 17 | 0 | A | |
| 2 | 20.5 | 0.9 | A | |
| 2 | 25.3 | 3.8 | BD | hose |
| 2 | 28.7 | 4.6 | BD | operator error |
| 1 | 41.8 | 14.7 | BD | bearing |
| 1 | 45.5 | 17.6 | A | |
| 2 | 48.6 | 22 | A | |
| 2 | 49.6 | 23.4 | BD | seal leak |
| 1 | 51.4 | 26.3 | A | |
| 1 | 58.2 | 35.7 | BD | seal leak |
| 2 | 59 | 36.5 | A | |
| 2 | 60.6 | 37.6 | BD | hose |
| 1 | 61.9 | 39.1 | BD | seal leak |
| 1 | 76.6 | 55.4 | BD | bearing |
| 2 | 81.1 | 61.1 | A | |
| 1 | 84.1 | 63.6 | A | |
| 1 | 84.7 | 64.3 | A | |
| 1 | 94.6 | 72.6 | A | |
| 2 | 100 | 78.1 | BD | valve |
| 1 | 104 | 81.4 | BD | bearing |
| 2 | 104.8 | 85.9 | BD | spring |
| 2 | 105.9 | 87.1 | BD | operator error |
| 1 | 108.8 | 89.9 | BD | hose |
| 2 | 132.4 | 119.5 | BD | spring |
| 2 | 132.4 | 150.1 | BD | operator error |
| 2 | 132.4 | 153.7 | A | |
Solution to Example 10
- 1) Figure CrowExtend9 shows the estimated Crow Extended parameters.
- 2) One possible method to calculate the projected MTBF and growth potential is to use the Quick Calculation Pad, but you can also view these two values at the same time by viewing the Growth Potential MTBF plot, which is displayed in Figure CrowExtend10. From the plot, the projected MTBF is equal to 16.87 hours and the growth potential is equal to 18.63 hours.
- 3) The current projected MTBF and growth potential MTBF are both well below the required goal of 30 hours. To check if this goal can even be reached, you can set the effectiveness factor equal to 1. In other words, if all of the corrective actions were to remove the failure modes completely then what would be the projected and growth potential MTBF? After changing the fixed effectiveness factor to 1, the parameters are recalculated and the Growth Potential plot is refreshed. The refreshed plot is shown in Figure CrowExtend11. Even if you assume an effectiveness factor equal to 1, the growth potential is still only 27.27 hours. Based on the current design process, it will not be possible to reach the MTBF goal of 30 hours. Therefore, there are basically two options: start a new design stage or reduce the required MTBF goal.
[math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math]
In a previous chapter, we discussed the most widely used traditional reliability growth tracking model, Crow-AMSAA (NHPP). Using this model for reliability growth analysis assumes that the corrective actions for the observed failure modes are incorporated during the test (test-fix-test). However, in actual practice, fixes may be delayed until after the completion of the test (test-find-test) or some fixes may be implemented during the test while others are delayed (test-fix-find-test). At the end of a test phase, two reliability estimates are of concern: demonstrated reliability and projected reliability. The demonstrated reliability, which is based on data generated during the test phase, is an estimate of the system reliability for its configuration at the end of the test phase. The projected reliability measures the impact of the delayed fixes at the end of the current test phase.
Most of the reliability growth literature has been concerned with procedures and models for calculating the demonstrated reliability and very little attention has been paid to techniques for reliability projections. The procedure for making reliability projections utilizes engineering assessments of the effectiveness of the delayed fixes for each observed failure mode. These effectiveness factors are then used with the data generated during the test phase to obtain a projected estimate for the updated configuration by adjusting the number of failures observed during the test phase. The process of estimating the projected reliability is accomplished using the Crow Extended model. The Crow Extended model allows for a flexible growth strategy that can include corrective actions performed during the test, as well as delayed corrective actions. The test-find-test and test-fix-find-test scenarios are simply subsets of the Crow Extended model.
Background
When a system is tested and failure modes are observed, management can make one of two possible decisions, either to fix or not fix the failure mode. Therefore, the management strategy places failure modes into two categories: A modes and B modes. A modes are all failure modes such that when seen during the test no corrective action will be taken. This accounts for all modes for which management determines that it is not economically or otherwise justified to take a corrective action. In order to provide the assessment and management metric structure for corrective actions during and after a test, two types of B modes are defined. BC modes are corrected during the test and the corrective actions for BD modes are delayed until the end of the test. The management strategy is defined by how the corrective actions, if any, will be implemented. In summary, the classifications are defined as follows:
- • A indicates that no corrective action was performed or will be performed (management chooses not to address for technical, financial or other reasons).
- • BC indicates that the corrective action was implemented during the test. The analysis assumes that the effect of the corrective action was experienced during the test (as with other test-fix-test reliability growth analyses).
- • BD indicates that the corrective action will be delayed until after the completion of the current test.
Figure CrowExtend1 shows an example of data entered for the Crow Extended model.
As you can see, each failure is indicated with A, BC, or BD in the Classification column. In addition, any number or text can be used to specify the mode. In Figure CrowExtend1, numbers were used in the Mode column for simplicity, but you could just as easily use Seal Leak, or whatever designation you deem appropriate for identifying the failure mode.
Reliability growth is achieved by decreasing the failure intensity. The failure intensity for the A failure modes will not change. Therefore, reliability growth can only be achieved by decreasing the BC and BD mode failure intensity. It is also clear that, in general, the only part of the BD mode failure intensity that can be decreased is that which has been seen during testing, since the failure intensity due to BD modes that were unseen during testing still remains. BC failure modes are corrected during test and the BC failure intensity will not change any more at the end of test.
It is very important to note that once a BD failure mode is in the system it is rarely totally eliminated by a corrective action. After a BD mode has been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will generally remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective you will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made and must be a value between 0 and 1. A study on EFs showed that an average EF [math]\displaystyle{ d }[/math] was about 70 percent. Therefore, typically about 30 percent, i.e. 100 [math]\displaystyle{ (1-d) }[/math] percent, of the BD mode failure intensity will remain in the system after all of the corrective actions have been implemented. However, individual EFs for the failure modes may be larger or smaller than the average. Figure efffact1 displays RGA's Effectiveness Factor window where the effectiveness factors for each unique BD failure mode can be specified.
Template loop detected: Template:Test-find-test rga
Template loop detected: Template:Test-fix-find-test rga
Template loop detected: Template:Failure mode management strategy rga
Template loop detected: Template:Confidence bounds crow extended rga
Template loop detected: Template:Grouped data rga
Template loop detected: Template:Mixed data rga
Template loop detected: Template:Multiple systems with event codes rga
General Examples
Example 8
Three systems were subjected to a reliability growth test to evaluate the prototype of a new product. Once the test was completed a failure analysis was done and, based on this, a management strategy was able to be defined. It was determined that all corrective actions will be delayed until after the test. The collected data set is shown in Table 9.6 and the associated effectiveness factors for each unique BD mode are presented in Table 9.7. The prototype is required to meet a projected MTBF goal of 55 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Based on the current management strategy what is the projected MTBF?
- 3) If the projected MTBF goal is not met, alter the current management strategy to meet this requirement with as little adjustment as possible and without changing the EFs of the existing BD modes. Assume an EF = 0.7 for any newly assigned BD modes.
| Table 9.6 - Multiple Systems (Concurrent Operating Times) data for Example 8 | |||
| System 1 | System 2 | System 3 | |
|---|---|---|---|
| Start Time | 0 | 0 | 0 |
| End Time | 541 | 454 | 436 |
| Times-to-Failure | 83 BD37 | 26 BD25 | 23 BD30 |
| 83 BD43 | 26 BD43 | 46 BD49 | |
| 83 BD46 | 57 BD37 | 127 BD47 | |
| 169 A45 | 64 BD19 | 166 A2 | |
| 213 A18 | 169 A45 | 169 BD23 | |
| 299 A42 | 213 A32 | 213 BD7 | |
| 375 A1 | 231 BD8 | 213 BD29 | |
| 431 BD16 | 231 BD25 | 255 BD26 | |
| 231 BD27 | 369 A33 | ||
| 231 A28 | 374 BD29 | ||
| 304 BD24 | 380 BD22 | ||
| 383 BD40 | 415 BD7 | ||
| Table 9.7 - Effectiveness factors for Example 8 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 30 | 0.75 |
| 43 | 0.5 |
| 25 | 0.5 |
| 49 | 0.75 |
| 37 | 0.9 |
| 19 | 0.75 |
| 46 | 0.75 |
| 47 | 0.25 |
| 23 | 0.5 |
| 7 | 0.25 |
| 29 | 0.25 |
| 8 | 0.5 |
| 27 | 0.5 |
| 26 | 0.75 |
| 24 | 0.5 |
| 22 | 0.5 |
| 40 | 0.75 |
| 16 | 0.75 |
Solution to Example 8
- 1) Figure CrowExtend2 shows the estimated Crow Extended parameters.
- 2) There are a couple of ways to calculate the projected MTBF, but the easiest is via the Quick Calculation Pad (QCP), as shown in Figure CrowExtend3.
- 3) From the previous question, the projected MTBF is estimated to be 53.9390 hours, which is below the goal of 55 hours. To reach our goal, or to see if we can even get there, the management strategy must be changed. The effectiveness factors for the existing BD modes cannot be changed, however it is possible to change an A mode to a BD mode. But which A mode(s) should be changed? To answer this question, you can view the Individual Mode Failure Intensity plot with just the A modes displayed as shown in Figure CrowExtend4. As you can see from the plot, failure mode A45 has the highest failure intensity. Therefore, among the A modes this particular failure mode is having the greatest negative effect in regards to the system MTBF. So change A45 to BD45. Be sure to change all instances of A45 to a BD mode. Enter an effectiveness factor for BD45 equal to 0.7 and recalculate the parameters of the Crow Extended model. Now go back to the QCP to calculate the projected MTBF as shown in Figure CrowExtend5. The projected MTBF is now estimated to be 55.5903 hours. Based on the change in the management strategy, the projected MTBF goal is now expected to be met.
Example 9
A reliability growth test was conducted for 200 hours. Some of the corrective actions were applied during the test while others were delayed until after the test was completed. The data set is given in Table 9.8. The effectiveness factors for the BD modes are given in Table 9.9. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Determine the average effectiveness factor of the BC modes using the Function Wizard.
- 3) What percent of the failure intensity will be left in the system due to the BD modes after implementing the delayed fixes?
| Table 9.8 - Grouped Failure Times data for Example 9 | |||
| Number at Event | Time to Event | Classification | Mode |
|---|---|---|---|
| 3 | 25 | BC | 1 |
| 1 | 25 | BD | 9 |
| 1 | 25 | BC | 2 |
| 1 | 50 | BD | 10 |
| 1 | 50 | BD | 11 |
| 1 | 75 | BD | 12 |
| 1 | 75 | BC | 3 |
| 2 | 75 | BD | 13 |
| 1 | 75 | A | |
| 1 | 100 | BC | 4 |
| 1 | 100 | BD | 14 |
| 1 | 125 | BD | 15 |
| 1 | 125 | A | |
| 1 | 125 | A | |
| 1 | 125 | BC | 5 |
| 1 | 125 | BD | 10 |
| 1 | 125 | BC | 6 |
| 1 | 150 | A | |
| 1 | 150 | BD | 16 |
| 1 | 175 | BC | 4 |
| 1 | 175 | BC | 8 |
| 1 | 175 | A | |
| 1 | 175 | BC | 7 |
| 1 | 200 | BD | 16 |
| 1 | 200 | BC | 3 |
| 1 | 200 | BD | 17 |
| Table 9.9 - Effectiveness factors for Example 9 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 9 | 0.75 |
| 10 | 0.5 |
| 11 | 0.9 |
| 12 | 0.6 |
| 13 | 0.8 |
| 14 | 0.8 |
| 15 | 0.25 |
| 16 | 0.75 |
| 17 | 0.8 |
Solution to Example 9
- 1) Figure CrowExtend6 shows the estimated parameters of the Crow Extended model.
- 2) After inserting a General Spreadsheet into the Folio, the Function Wizard can be accessed via the Tools menu. Once the Function Wizard is loaded, select Average Effectiveness Factor from the list of available functions and under Avg. Eff. Factor select BC modes as shown in Figure CrowExtend7. Click OK and the result will be placed into the General Spreadsheet. The average effectiveness factor for the BC modes is 0.6983.
- 3) The percent of the failure intensity left in the system due to the BD modes can be determined using the Failure Mode Strategy plot as shown in Figure CrowExtend8. Therefore, the percent of the failure intensity left in the system due to the BD modes is 1.79%.
Example 10
Two prototypes of a new design are tested simultaneously. Whenever a failure was observed for one unit, the current operating time of the other unit was also recorded. The test was terminated after 300 hours. All of the design changes for the prototypes were delayed until after completing the test and the data set is given in Table 9.10. Assume a fixed effectiveness factor equal to 0.7. The MTBF goal for the new design is 30 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) What is the projected MTBF and growth potential?
- 3) Under the current management strategy, is it even possible to reach the MTBF goal of 30 hours?
| Table 9.10 - Multiple Systems (Known Operating Times) data for Example 10 | ||||
| Failed Unit ID | Time Unit 1 | Time Unit 2 | Classification | Mode |
|---|---|---|---|---|
| 1 | 16.5 | 0 | BD | seal leak |
| 1 | 16.5 | 0 | BD | valve |
| 1 | 17 | 0 | A | |
| 2 | 20.5 | 0.9 | A | |
| 2 | 25.3 | 3.8 | BD | hose |
| 2 | 28.7 | 4.6 | BD | operator error |
| 1 | 41.8 | 14.7 | BD | bearing |
| 1 | 45.5 | 17.6 | A | |
| 2 | 48.6 | 22 | A | |
| 2 | 49.6 | 23.4 | BD | seal leak |
| 1 | 51.4 | 26.3 | A | |
| 1 | 58.2 | 35.7 | BD | seal leak |
| 2 | 59 | 36.5 | A | |
| 2 | 60.6 | 37.6 | BD | hose |
| 1 | 61.9 | 39.1 | BD | seal leak |
| 1 | 76.6 | 55.4 | BD | bearing |
| 2 | 81.1 | 61.1 | A | |
| 1 | 84.1 | 63.6 | A | |
| 1 | 84.7 | 64.3 | A | |
| 1 | 94.6 | 72.6 | A | |
| 2 | 100 | 78.1 | BD | valve |
| 1 | 104 | 81.4 | BD | bearing |
| 2 | 104.8 | 85.9 | BD | spring |
| 2 | 105.9 | 87.1 | BD | operator error |
| 1 | 108.8 | 89.9 | BD | hose |
| 2 | 132.4 | 119.5 | BD | spring |
| 2 | 132.4 | 150.1 | BD | operator error |
| 2 | 132.4 | 153.7 | A | |
Solution to Example 10
- 1) Figure CrowExtend9 shows the estimated Crow Extended parameters.
- 2) One possible method to calculate the projected MTBF and growth potential is to use the Quick Calculation Pad, but you can also view these two values at the same time by viewing the Growth Potential MTBF plot, which is displayed in Figure CrowExtend10. From the plot, the projected MTBF is equal to 16.87 hours and the growth potential is equal to 18.63 hours.
- 3) The current projected MTBF and growth potential MTBF are both well below the required goal of 30 hours. To check if this goal can even be reached, you can set the effectiveness factor equal to 1. In other words, if all of the corrective actions were to remove the failure modes completely then what would be the projected and growth potential MTBF? After changing the fixed effectiveness factor to 1, the parameters are recalculated and the Growth Potential plot is refreshed. The refreshed plot is shown in Figure CrowExtend11. Even if you assume an effectiveness factor equal to 1, the growth potential is still only 27.27 hours. Based on the current design process, it will not be possible to reach the MTBF goal of 30 hours. Therefore, there are basically two options: start a new design stage or reduce the required MTBF goal.
[math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math]
In a previous chapter, we discussed the most widely used traditional reliability growth tracking model, Crow-AMSAA (NHPP). Using this model for reliability growth analysis assumes that the corrective actions for the observed failure modes are incorporated during the test (test-fix-test). However, in actual practice, fixes may be delayed until after the completion of the test (test-find-test) or some fixes may be implemented during the test while others are delayed (test-fix-find-test). At the end of a test phase, two reliability estimates are of concern: demonstrated reliability and projected reliability. The demonstrated reliability, which is based on data generated during the test phase, is an estimate of the system reliability for its configuration at the end of the test phase. The projected reliability measures the impact of the delayed fixes at the end of the current test phase.
Most of the reliability growth literature has been concerned with procedures and models for calculating the demonstrated reliability and very little attention has been paid to techniques for reliability projections. The procedure for making reliability projections utilizes engineering assessments of the effectiveness of the delayed fixes for each observed failure mode. These effectiveness factors are then used with the data generated during the test phase to obtain a projected estimate for the updated configuration by adjusting the number of failures observed during the test phase. The process of estimating the projected reliability is accomplished using the Crow Extended model. The Crow Extended model allows for a flexible growth strategy that can include corrective actions performed during the test, as well as delayed corrective actions. The test-find-test and test-fix-find-test scenarios are simply subsets of the Crow Extended model.
Background
When a system is tested and failure modes are observed, management can make one of two possible decisions, either to fix or not fix the failure mode. Therefore, the management strategy places failure modes into two categories: A modes and B modes. A modes are all failure modes such that when seen during the test no corrective action will be taken. This accounts for all modes for which management determines that it is not economically or otherwise justified to take a corrective action. In order to provide the assessment and management metric structure for corrective actions during and after a test, two types of B modes are defined. BC modes are corrected during the test and the corrective actions for BD modes are delayed until the end of the test. The management strategy is defined by how the corrective actions, if any, will be implemented. In summary, the classifications are defined as follows:
- • A indicates that no corrective action was performed or will be performed (management chooses not to address for technical, financial or other reasons).
- • BC indicates that the corrective action was implemented during the test. The analysis assumes that the effect of the corrective action was experienced during the test (as with other test-fix-test reliability growth analyses).
- • BD indicates that the corrective action will be delayed until after the completion of the current test.
Figure CrowExtend1 shows an example of data entered for the Crow Extended model.
As you can see, each failure is indicated with A, BC, or BD in the Classification column. In addition, any number or text can be used to specify the mode. In Figure CrowExtend1, numbers were used in the Mode column for simplicity, but you could just as easily use Seal Leak, or whatever designation you deem appropriate for identifying the failure mode.
Reliability growth is achieved by decreasing the failure intensity. The failure intensity for the A failure modes will not change. Therefore, reliability growth can only be achieved by decreasing the BC and BD mode failure intensity. It is also clear that, in general, the only part of the BD mode failure intensity that can be decreased is that which has been seen during testing, since the failure intensity due to BD modes that were unseen during testing still remains. BC failure modes are corrected during test and the BC failure intensity will not change any more at the end of test.
It is very important to note that once a BD failure mode is in the system it is rarely totally eliminated by a corrective action. After a BD mode has been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will generally remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective you will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made and must be a value between 0 and 1. A study on EFs showed that an average EF [math]\displaystyle{ d }[/math] was about 70 percent. Therefore, typically about 30 percent, i.e. 100 [math]\displaystyle{ (1-d) }[/math] percent, of the BD mode failure intensity will remain in the system after all of the corrective actions have been implemented. However, individual EFs for the failure modes may be larger or smaller than the average. Figure efffact1 displays RGA's Effectiveness Factor window where the effectiveness factors for each unique BD failure mode can be specified.
Template loop detected: Template:Test-find-test rga
Template loop detected: Template:Test-fix-find-test rga
Template loop detected: Template:Failure mode management strategy rga
Template loop detected: Template:Confidence bounds crow extended rga
Template loop detected: Template:Grouped data rga
Template loop detected: Template:Mixed data rga
Template loop detected: Template:Multiple systems with event codes rga
General Examples
Example 8
Three systems were subjected to a reliability growth test to evaluate the prototype of a new product. Once the test was completed a failure analysis was done and, based on this, a management strategy was able to be defined. It was determined that all corrective actions will be delayed until after the test. The collected data set is shown in Table 9.6 and the associated effectiveness factors for each unique BD mode are presented in Table 9.7. The prototype is required to meet a projected MTBF goal of 55 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Based on the current management strategy what is the projected MTBF?
- 3) If the projected MTBF goal is not met, alter the current management strategy to meet this requirement with as little adjustment as possible and without changing the EFs of the existing BD modes. Assume an EF = 0.7 for any newly assigned BD modes.
| Table 9.6 - Multiple Systems (Concurrent Operating Times) data for Example 8 | |||
| System 1 | System 2 | System 3 | |
|---|---|---|---|
| Start Time | 0 | 0 | 0 |
| End Time | 541 | 454 | 436 |
| Times-to-Failure | 83 BD37 | 26 BD25 | 23 BD30 |
| 83 BD43 | 26 BD43 | 46 BD49 | |
| 83 BD46 | 57 BD37 | 127 BD47 | |
| 169 A45 | 64 BD19 | 166 A2 | |
| 213 A18 | 169 A45 | 169 BD23 | |
| 299 A42 | 213 A32 | 213 BD7 | |
| 375 A1 | 231 BD8 | 213 BD29 | |
| 431 BD16 | 231 BD25 | 255 BD26 | |
| 231 BD27 | 369 A33 | ||
| 231 A28 | 374 BD29 | ||
| 304 BD24 | 380 BD22 | ||
| 383 BD40 | 415 BD7 | ||
| Table 9.7 - Effectiveness factors for Example 8 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 30 | 0.75 |
| 43 | 0.5 |
| 25 | 0.5 |
| 49 | 0.75 |
| 37 | 0.9 |
| 19 | 0.75 |
| 46 | 0.75 |
| 47 | 0.25 |
| 23 | 0.5 |
| 7 | 0.25 |
| 29 | 0.25 |
| 8 | 0.5 |
| 27 | 0.5 |
| 26 | 0.75 |
| 24 | 0.5 |
| 22 | 0.5 |
| 40 | 0.75 |
| 16 | 0.75 |
Solution to Example 8
- 1) Figure CrowExtend2 shows the estimated Crow Extended parameters.
- 2) There are a couple of ways to calculate the projected MTBF, but the easiest is via the Quick Calculation Pad (QCP), as shown in Figure CrowExtend3.
- 3) From the previous question, the projected MTBF is estimated to be 53.9390 hours, which is below the goal of 55 hours. To reach our goal, or to see if we can even get there, the management strategy must be changed. The effectiveness factors for the existing BD modes cannot be changed, however it is possible to change an A mode to a BD mode. But which A mode(s) should be changed? To answer this question, you can view the Individual Mode Failure Intensity plot with just the A modes displayed as shown in Figure CrowExtend4. As you can see from the plot, failure mode A45 has the highest failure intensity. Therefore, among the A modes this particular failure mode is having the greatest negative effect in regards to the system MTBF. So change A45 to BD45. Be sure to change all instances of A45 to a BD mode. Enter an effectiveness factor for BD45 equal to 0.7 and recalculate the parameters of the Crow Extended model. Now go back to the QCP to calculate the projected MTBF as shown in Figure CrowExtend5. The projected MTBF is now estimated to be 55.5903 hours. Based on the change in the management strategy, the projected MTBF goal is now expected to be met.
Example 9
A reliability growth test was conducted for 200 hours. Some of the corrective actions were applied during the test while others were delayed until after the test was completed. The data set is given in Table 9.8. The effectiveness factors for the BD modes are given in Table 9.9. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Determine the average effectiveness factor of the BC modes using the Function Wizard.
- 3) What percent of the failure intensity will be left in the system due to the BD modes after implementing the delayed fixes?
| Table 9.8 - Grouped Failure Times data for Example 9 | |||
| Number at Event | Time to Event | Classification | Mode |
|---|---|---|---|
| 3 | 25 | BC | 1 |
| 1 | 25 | BD | 9 |
| 1 | 25 | BC | 2 |
| 1 | 50 | BD | 10 |
| 1 | 50 | BD | 11 |
| 1 | 75 | BD | 12 |
| 1 | 75 | BC | 3 |
| 2 | 75 | BD | 13 |
| 1 | 75 | A | |
| 1 | 100 | BC | 4 |
| 1 | 100 | BD | 14 |
| 1 | 125 | BD | 15 |
| 1 | 125 | A | |
| 1 | 125 | A | |
| 1 | 125 | BC | 5 |
| 1 | 125 | BD | 10 |
| 1 | 125 | BC | 6 |
| 1 | 150 | A | |
| 1 | 150 | BD | 16 |
| 1 | 175 | BC | 4 |
| 1 | 175 | BC | 8 |
| 1 | 175 | A | |
| 1 | 175 | BC | 7 |
| 1 | 200 | BD | 16 |
| 1 | 200 | BC | 3 |
| 1 | 200 | BD | 17 |
| Table 9.9 - Effectiveness factors for Example 9 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 9 | 0.75 |
| 10 | 0.5 |
| 11 | 0.9 |
| 12 | 0.6 |
| 13 | 0.8 |
| 14 | 0.8 |
| 15 | 0.25 |
| 16 | 0.75 |
| 17 | 0.8 |
Solution to Example 9
- 1) Figure CrowExtend6 shows the estimated parameters of the Crow Extended model.
- 2) After inserting a General Spreadsheet into the Folio, the Function Wizard can be accessed via the Tools menu. Once the Function Wizard is loaded, select Average Effectiveness Factor from the list of available functions and under Avg. Eff. Factor select BC modes as shown in Figure CrowExtend7. Click OK and the result will be placed into the General Spreadsheet. The average effectiveness factor for the BC modes is 0.6983.
- 3) The percent of the failure intensity left in the system due to the BD modes can be determined using the Failure Mode Strategy plot as shown in Figure CrowExtend8. Therefore, the percent of the failure intensity left in the system due to the BD modes is 1.79%.
Example 10
Two prototypes of a new design are tested simultaneously. Whenever a failure was observed for one unit, the current operating time of the other unit was also recorded. The test was terminated after 300 hours. All of the design changes for the prototypes were delayed until after completing the test and the data set is given in Table 9.10. Assume a fixed effectiveness factor equal to 0.7. The MTBF goal for the new design is 30 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) What is the projected MTBF and growth potential?
- 3) Under the current management strategy, is it even possible to reach the MTBF goal of 30 hours?
| Table 9.10 - Multiple Systems (Known Operating Times) data for Example 10 | ||||
| Failed Unit ID | Time Unit 1 | Time Unit 2 | Classification | Mode |
|---|---|---|---|---|
| 1 | 16.5 | 0 | BD | seal leak |
| 1 | 16.5 | 0 | BD | valve |
| 1 | 17 | 0 | A | |
| 2 | 20.5 | 0.9 | A | |
| 2 | 25.3 | 3.8 | BD | hose |
| 2 | 28.7 | 4.6 | BD | operator error |
| 1 | 41.8 | 14.7 | BD | bearing |
| 1 | 45.5 | 17.6 | A | |
| 2 | 48.6 | 22 | A | |
| 2 | 49.6 | 23.4 | BD | seal leak |
| 1 | 51.4 | 26.3 | A | |
| 1 | 58.2 | 35.7 | BD | seal leak |
| 2 | 59 | 36.5 | A | |
| 2 | 60.6 | 37.6 | BD | hose |
| 1 | 61.9 | 39.1 | BD | seal leak |
| 1 | 76.6 | 55.4 | BD | bearing |
| 2 | 81.1 | 61.1 | A | |
| 1 | 84.1 | 63.6 | A | |
| 1 | 84.7 | 64.3 | A | |
| 1 | 94.6 | 72.6 | A | |
| 2 | 100 | 78.1 | BD | valve |
| 1 | 104 | 81.4 | BD | bearing |
| 2 | 104.8 | 85.9 | BD | spring |
| 2 | 105.9 | 87.1 | BD | operator error |
| 1 | 108.8 | 89.9 | BD | hose |
| 2 | 132.4 | 119.5 | BD | spring |
| 2 | 132.4 | 150.1 | BD | operator error |
| 2 | 132.4 | 153.7 | A | |
Solution to Example 10
- 1) Figure CrowExtend9 shows the estimated Crow Extended parameters.
- 2) One possible method to calculate the projected MTBF and growth potential is to use the Quick Calculation Pad, but you can also view these two values at the same time by viewing the Growth Potential MTBF plot, which is displayed in Figure CrowExtend10. From the plot, the projected MTBF is equal to 16.87 hours and the growth potential is equal to 18.63 hours.
- 3) The current projected MTBF and growth potential MTBF are both well below the required goal of 30 hours. To check if this goal can even be reached, you can set the effectiveness factor equal to 1. In other words, if all of the corrective actions were to remove the failure modes completely then what would be the projected and growth potential MTBF? After changing the fixed effectiveness factor to 1, the parameters are recalculated and the Growth Potential plot is refreshed. The refreshed plot is shown in Figure CrowExtend11. Even if you assume an effectiveness factor equal to 1, the growth potential is still only 27.27 hours. Based on the current design process, it will not be possible to reach the MTBF goal of 30 hours. Therefore, there are basically two options: start a new design stage or reduce the required MTBF goal.
[math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math]
In a previous chapter, we discussed the most widely used traditional reliability growth tracking model, Crow-AMSAA (NHPP). Using this model for reliability growth analysis assumes that the corrective actions for the observed failure modes are incorporated during the test (test-fix-test). However, in actual practice, fixes may be delayed until after the completion of the test (test-find-test) or some fixes may be implemented during the test while others are delayed (test-fix-find-test). At the end of a test phase, two reliability estimates are of concern: demonstrated reliability and projected reliability. The demonstrated reliability, which is based on data generated during the test phase, is an estimate of the system reliability for its configuration at the end of the test phase. The projected reliability measures the impact of the delayed fixes at the end of the current test phase.
Most of the reliability growth literature has been concerned with procedures and models for calculating the demonstrated reliability and very little attention has been paid to techniques for reliability projections. The procedure for making reliability projections utilizes engineering assessments of the effectiveness of the delayed fixes for each observed failure mode. These effectiveness factors are then used with the data generated during the test phase to obtain a projected estimate for the updated configuration by adjusting the number of failures observed during the test phase. The process of estimating the projected reliability is accomplished using the Crow Extended model. The Crow Extended model allows for a flexible growth strategy that can include corrective actions performed during the test, as well as delayed corrective actions. The test-find-test and test-fix-find-test scenarios are simply subsets of the Crow Extended model.
Background
When a system is tested and failure modes are observed, management can make one of two possible decisions, either to fix or not fix the failure mode. Therefore, the management strategy places failure modes into two categories: A modes and B modes. A modes are all failure modes such that when seen during the test no corrective action will be taken. This accounts for all modes for which management determines that it is not economically or otherwise justified to take a corrective action. In order to provide the assessment and management metric structure for corrective actions during and after a test, two types of B modes are defined. BC modes are corrected during the test and the corrective actions for BD modes are delayed until the end of the test. The management strategy is defined by how the corrective actions, if any, will be implemented. In summary, the classifications are defined as follows:
- • A indicates that no corrective action was performed or will be performed (management chooses not to address for technical, financial or other reasons).
- • BC indicates that the corrective action was implemented during the test. The analysis assumes that the effect of the corrective action was experienced during the test (as with other test-fix-test reliability growth analyses).
- • BD indicates that the corrective action will be delayed until after the completion of the current test.
Figure CrowExtend1 shows an example of data entered for the Crow Extended model.
As you can see, each failure is indicated with A, BC, or BD in the Classification column. In addition, any number or text can be used to specify the mode. In Figure CrowExtend1, numbers were used in the Mode column for simplicity, but you could just as easily use Seal Leak, or whatever designation you deem appropriate for identifying the failure mode.
Reliability growth is achieved by decreasing the failure intensity. The failure intensity for the A failure modes will not change. Therefore, reliability growth can only be achieved by decreasing the BC and BD mode failure intensity. It is also clear that, in general, the only part of the BD mode failure intensity that can be decreased is that which has been seen during testing, since the failure intensity due to BD modes that were unseen during testing still remains. BC failure modes are corrected during test and the BC failure intensity will not change any more at the end of test.
It is very important to note that once a BD failure mode is in the system it is rarely totally eliminated by a corrective action. After a BD mode has been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will generally remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective you will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made and must be a value between 0 and 1. A study on EFs showed that an average EF [math]\displaystyle{ d }[/math] was about 70 percent. Therefore, typically about 30 percent, i.e. 100 [math]\displaystyle{ (1-d) }[/math] percent, of the BD mode failure intensity will remain in the system after all of the corrective actions have been implemented. However, individual EFs for the failure modes may be larger or smaller than the average. Figure efffact1 displays RGA's Effectiveness Factor window where the effectiveness factors for each unique BD failure mode can be specified.
Template loop detected: Template:Test-find-test rga
Template loop detected: Template:Test-fix-find-test rga
Template loop detected: Template:Failure mode management strategy rga
Template loop detected: Template:Confidence bounds crow extended rga
Template loop detected: Template:Grouped data rga
Template loop detected: Template:Mixed data rga
Template loop detected: Template:Multiple systems with event codes rga
General Examples
Example 8
Three systems were subjected to a reliability growth test to evaluate the prototype of a new product. Once the test was completed a failure analysis was done and, based on this, a management strategy was able to be defined. It was determined that all corrective actions will be delayed until after the test. The collected data set is shown in Table 9.6 and the associated effectiveness factors for each unique BD mode are presented in Table 9.7. The prototype is required to meet a projected MTBF goal of 55 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Based on the current management strategy what is the projected MTBF?
- 3) If the projected MTBF goal is not met, alter the current management strategy to meet this requirement with as little adjustment as possible and without changing the EFs of the existing BD modes. Assume an EF = 0.7 for any newly assigned BD modes.
| Table 9.6 - Multiple Systems (Concurrent Operating Times) data for Example 8 | |||
| System 1 | System 2 | System 3 | |
|---|---|---|---|
| Start Time | 0 | 0 | 0 |
| End Time | 541 | 454 | 436 |
| Times-to-Failure | 83 BD37 | 26 BD25 | 23 BD30 |
| 83 BD43 | 26 BD43 | 46 BD49 | |
| 83 BD46 | 57 BD37 | 127 BD47 | |
| 169 A45 | 64 BD19 | 166 A2 | |
| 213 A18 | 169 A45 | 169 BD23 | |
| 299 A42 | 213 A32 | 213 BD7 | |
| 375 A1 | 231 BD8 | 213 BD29 | |
| 431 BD16 | 231 BD25 | 255 BD26 | |
| 231 BD27 | 369 A33 | ||
| 231 A28 | 374 BD29 | ||
| 304 BD24 | 380 BD22 | ||
| 383 BD40 | 415 BD7 | ||
| Table 9.7 - Effectiveness factors for Example 8 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 30 | 0.75 |
| 43 | 0.5 |
| 25 | 0.5 |
| 49 | 0.75 |
| 37 | 0.9 |
| 19 | 0.75 |
| 46 | 0.75 |
| 47 | 0.25 |
| 23 | 0.5 |
| 7 | 0.25 |
| 29 | 0.25 |
| 8 | 0.5 |
| 27 | 0.5 |
| 26 | 0.75 |
| 24 | 0.5 |
| 22 | 0.5 |
| 40 | 0.75 |
| 16 | 0.75 |
Solution to Example 8
- 1) Figure CrowExtend2 shows the estimated Crow Extended parameters.
- 2) There are a couple of ways to calculate the projected MTBF, but the easiest is via the Quick Calculation Pad (QCP), as shown in Figure CrowExtend3.
- 3) From the previous question, the projected MTBF is estimated to be 53.9390 hours, which is below the goal of 55 hours. To reach our goal, or to see if we can even get there, the management strategy must be changed. The effectiveness factors for the existing BD modes cannot be changed, however it is possible to change an A mode to a BD mode. But which A mode(s) should be changed? To answer this question, you can view the Individual Mode Failure Intensity plot with just the A modes displayed as shown in Figure CrowExtend4. As you can see from the plot, failure mode A45 has the highest failure intensity. Therefore, among the A modes this particular failure mode is having the greatest negative effect in regards to the system MTBF. So change A45 to BD45. Be sure to change all instances of A45 to a BD mode. Enter an effectiveness factor for BD45 equal to 0.7 and recalculate the parameters of the Crow Extended model. Now go back to the QCP to calculate the projected MTBF as shown in Figure CrowExtend5. The projected MTBF is now estimated to be 55.5903 hours. Based on the change in the management strategy, the projected MTBF goal is now expected to be met.
Example 9
A reliability growth test was conducted for 200 hours. Some of the corrective actions were applied during the test while others were delayed until after the test was completed. The data set is given in Table 9.8. The effectiveness factors for the BD modes are given in Table 9.9. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Determine the average effectiveness factor of the BC modes using the Function Wizard.
- 3) What percent of the failure intensity will be left in the system due to the BD modes after implementing the delayed fixes?
| Table 9.8 - Grouped Failure Times data for Example 9 | |||
| Number at Event | Time to Event | Classification | Mode |
|---|---|---|---|
| 3 | 25 | BC | 1 |
| 1 | 25 | BD | 9 |
| 1 | 25 | BC | 2 |
| 1 | 50 | BD | 10 |
| 1 | 50 | BD | 11 |
| 1 | 75 | BD | 12 |
| 1 | 75 | BC | 3 |
| 2 | 75 | BD | 13 |
| 1 | 75 | A | |
| 1 | 100 | BC | 4 |
| 1 | 100 | BD | 14 |
| 1 | 125 | BD | 15 |
| 1 | 125 | A | |
| 1 | 125 | A | |
| 1 | 125 | BC | 5 |
| 1 | 125 | BD | 10 |
| 1 | 125 | BC | 6 |
| 1 | 150 | A | |
| 1 | 150 | BD | 16 |
| 1 | 175 | BC | 4 |
| 1 | 175 | BC | 8 |
| 1 | 175 | A | |
| 1 | 175 | BC | 7 |
| 1 | 200 | BD | 16 |
| 1 | 200 | BC | 3 |
| 1 | 200 | BD | 17 |
| Table 9.9 - Effectiveness factors for Example 9 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 9 | 0.75 |
| 10 | 0.5 |
| 11 | 0.9 |
| 12 | 0.6 |
| 13 | 0.8 |
| 14 | 0.8 |
| 15 | 0.25 |
| 16 | 0.75 |
| 17 | 0.8 |
Solution to Example 9
- 1) Figure CrowExtend6 shows the estimated parameters of the Crow Extended model.
- 2) After inserting a General Spreadsheet into the Folio, the Function Wizard can be accessed via the Tools menu. Once the Function Wizard is loaded, select Average Effectiveness Factor from the list of available functions and under Avg. Eff. Factor select BC modes as shown in Figure CrowExtend7. Click OK and the result will be placed into the General Spreadsheet. The average effectiveness factor for the BC modes is 0.6983.
- 3) The percent of the failure intensity left in the system due to the BD modes can be determined using the Failure Mode Strategy plot as shown in Figure CrowExtend8. Therefore, the percent of the failure intensity left in the system due to the BD modes is 1.79%.
Example 10
Two prototypes of a new design are tested simultaneously. Whenever a failure was observed for one unit, the current operating time of the other unit was also recorded. The test was terminated after 300 hours. All of the design changes for the prototypes were delayed until after completing the test and the data set is given in Table 9.10. Assume a fixed effectiveness factor equal to 0.7. The MTBF goal for the new design is 30 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) What is the projected MTBF and growth potential?
- 3) Under the current management strategy, is it even possible to reach the MTBF goal of 30 hours?
| Table 9.10 - Multiple Systems (Known Operating Times) data for Example 10 | ||||
| Failed Unit ID | Time Unit 1 | Time Unit 2 | Classification | Mode |
|---|---|---|---|---|
| 1 | 16.5 | 0 | BD | seal leak |
| 1 | 16.5 | 0 | BD | valve |
| 1 | 17 | 0 | A | |
| 2 | 20.5 | 0.9 | A | |
| 2 | 25.3 | 3.8 | BD | hose |
| 2 | 28.7 | 4.6 | BD | operator error |
| 1 | 41.8 | 14.7 | BD | bearing |
| 1 | 45.5 | 17.6 | A | |
| 2 | 48.6 | 22 | A | |
| 2 | 49.6 | 23.4 | BD | seal leak |
| 1 | 51.4 | 26.3 | A | |
| 1 | 58.2 | 35.7 | BD | seal leak |
| 2 | 59 | 36.5 | A | |
| 2 | 60.6 | 37.6 | BD | hose |
| 1 | 61.9 | 39.1 | BD | seal leak |
| 1 | 76.6 | 55.4 | BD | bearing |
| 2 | 81.1 | 61.1 | A | |
| 1 | 84.1 | 63.6 | A | |
| 1 | 84.7 | 64.3 | A | |
| 1 | 94.6 | 72.6 | A | |
| 2 | 100 | 78.1 | BD | valve |
| 1 | 104 | 81.4 | BD | bearing |
| 2 | 104.8 | 85.9 | BD | spring |
| 2 | 105.9 | 87.1 | BD | operator error |
| 1 | 108.8 | 89.9 | BD | hose |
| 2 | 132.4 | 119.5 | BD | spring |
| 2 | 132.4 | 150.1 | BD | operator error |
| 2 | 132.4 | 153.7 | A | |
Solution to Example 10
- 1) Figure CrowExtend9 shows the estimated Crow Extended parameters.
- 2) One possible method to calculate the projected MTBF and growth potential is to use the Quick Calculation Pad, but you can also view these two values at the same time by viewing the Growth Potential MTBF plot, which is displayed in Figure CrowExtend10. From the plot, the projected MTBF is equal to 16.87 hours and the growth potential is equal to 18.63 hours.
- 3) The current projected MTBF and growth potential MTBF are both well below the required goal of 30 hours. To check if this goal can even be reached, you can set the effectiveness factor equal to 1. In other words, if all of the corrective actions were to remove the failure modes completely then what would be the projected and growth potential MTBF? After changing the fixed effectiveness factor to 1, the parameters are recalculated and the Growth Potential plot is refreshed. The refreshed plot is shown in Figure CrowExtend11. Even if you assume an effectiveness factor equal to 1, the growth potential is still only 27.27 hours. Based on the current design process, it will not be possible to reach the MTBF goal of 30 hours. Therefore, there are basically two options: start a new design stage or reduce the required MTBF goal.
[math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math]
General Examples
Example 8
Three systems were subjected to a reliability growth test to evaluate the prototype of a new product. Once the test was completed a failure analysis was done and, based on this, a management strategy was able to be defined. It was determined that all corrective actions will be delayed until after the test. The collected data set is shown in Table 9.6 and the associated effectiveness factors for each unique BD mode are presented in Table 9.7. The prototype is required to meet a projected MTBF goal of 55 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Based on the current management strategy what is the projected MTBF?
- 3) If the projected MTBF goal is not met, alter the current management strategy to meet this requirement with as little adjustment as possible and without changing the EFs of the existing BD modes. Assume an EF = 0.7 for any newly assigned BD modes.
| Table 9.6 - Multiple Systems (Concurrent Operating Times) data for Example 8 | |||
| System 1 | System 2 | System 3 | |
|---|---|---|---|
| Start Time | 0 | 0 | 0 |
| End Time | 541 | 454 | 436 |
| Times-to-Failure | 83 BD37 | 26 BD25 | 23 BD30 |
| 83 BD43 | 26 BD43 | 46 BD49 | |
| 83 BD46 | 57 BD37 | 127 BD47 | |
| 169 A45 | 64 BD19 | 166 A2 | |
| 213 A18 | 169 A45 | 169 BD23 | |
| 299 A42 | 213 A32 | 213 BD7 | |
| 375 A1 | 231 BD8 | 213 BD29 | |
| 431 BD16 | 231 BD25 | 255 BD26 | |
| 231 BD27 | 369 A33 | ||
| 231 A28 | 374 BD29 | ||
| 304 BD24 | 380 BD22 | ||
| 383 BD40 | 415 BD7 | ||
| Table 9.7 - Effectiveness factors for Example 8 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 30 | 0.75 |
| 43 | 0.5 |
| 25 | 0.5 |
| 49 | 0.75 |
| 37 | 0.9 |
| 19 | 0.75 |
| 46 | 0.75 |
| 47 | 0.25 |
| 23 | 0.5 |
| 7 | 0.25 |
| 29 | 0.25 |
| 8 | 0.5 |
| 27 | 0.5 |
| 26 | 0.75 |
| 24 | 0.5 |
| 22 | 0.5 |
| 40 | 0.75 |
| 16 | 0.75 |
Solution to Example 8
- 1) Figure CrowExtend2 shows the estimated Crow Extended parameters.
- 2) There are a couple of ways to calculate the projected MTBF, but the easiest is via the Quick Calculation Pad (QCP), as shown in Figure CrowExtend3.
- 3) From the previous question, the projected MTBF is estimated to be 53.9390 hours, which is below the goal of 55 hours. To reach our goal, or to see if we can even get there, the management strategy must be changed. The effectiveness factors for the existing BD modes cannot be changed, however it is possible to change an A mode to a BD mode. But which A mode(s) should be changed? To answer this question, you can view the Individual Mode Failure Intensity plot with just the A modes displayed as shown in Figure CrowExtend4. As you can see from the plot, failure mode A45 has the highest failure intensity. Therefore, among the A modes this particular failure mode is having the greatest negative effect in regards to the system MTBF. So change A45 to BD45. Be sure to change all instances of A45 to a BD mode. Enter an effectiveness factor for BD45 equal to 0.7 and recalculate the parameters of the Crow Extended model. Now go back to the QCP to calculate the projected MTBF as shown in Figure CrowExtend5. The projected MTBF is now estimated to be 55.5903 hours. Based on the change in the management strategy, the projected MTBF goal is now expected to be met.
Example 9
A reliability growth test was conducted for 200 hours. Some of the corrective actions were applied during the test while others were delayed until after the test was completed. The data set is given in Table 9.8. The effectiveness factors for the BD modes are given in Table 9.9. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) Determine the average effectiveness factor of the BC modes using the Function Wizard.
- 3) What percent of the failure intensity will be left in the system due to the BD modes after implementing the delayed fixes?
| Table 9.8 - Grouped Failure Times data for Example 9 | |||
| Number at Event | Time to Event | Classification | Mode |
|---|---|---|---|
| 3 | 25 | BC | 1 |
| 1 | 25 | BD | 9 |
| 1 | 25 | BC | 2 |
| 1 | 50 | BD | 10 |
| 1 | 50 | BD | 11 |
| 1 | 75 | BD | 12 |
| 1 | 75 | BC | 3 |
| 2 | 75 | BD | 13 |
| 1 | 75 | A | |
| 1 | 100 | BC | 4 |
| 1 | 100 | BD | 14 |
| 1 | 125 | BD | 15 |
| 1 | 125 | A | |
| 1 | 125 | A | |
| 1 | 125 | BC | 5 |
| 1 | 125 | BD | 10 |
| 1 | 125 | BC | 6 |
| 1 | 150 | A | |
| 1 | 150 | BD | 16 |
| 1 | 175 | BC | 4 |
| 1 | 175 | BC | 8 |
| 1 | 175 | A | |
| 1 | 175 | BC | 7 |
| 1 | 200 | BD | 16 |
| 1 | 200 | BC | 3 |
| 1 | 200 | BD | 17 |
| Table 9.9 - Effectiveness factors for Example 9 | |
| BD Mode | Effectiveness Factor |
|---|---|
| 9 | 0.75 |
| 10 | 0.5 |
| 11 | 0.9 |
| 12 | 0.6 |
| 13 | 0.8 |
| 14 | 0.8 |
| 15 | 0.25 |
| 16 | 0.75 |
| 17 | 0.8 |
Solution to Example 9
- 1) Figure CrowExtend6 shows the estimated parameters of the Crow Extended model.
- 2) After inserting a General Spreadsheet into the Folio, the Function Wizard can be accessed via the Tools menu. Once the Function Wizard is loaded, select Average Effectiveness Factor from the list of available functions and under Avg. Eff. Factor select BC modes as shown in Figure CrowExtend7. Click OK and the result will be placed into the General Spreadsheet. The average effectiveness factor for the BC modes is 0.6983.
- 3) The percent of the failure intensity left in the system due to the BD modes can be determined using the Failure Mode Strategy plot as shown in Figure CrowExtend8. Therefore, the percent of the failure intensity left in the system due to the BD modes is 1.79%.
Example 10
Two prototypes of a new design are tested simultaneously. Whenever a failure was observed for one unit, the current operating time of the other unit was also recorded. The test was terminated after 300 hours. All of the design changes for the prototypes were delayed until after completing the test and the data set is given in Table 9.10. Assume a fixed effectiveness factor equal to 0.7. The MTBF goal for the new design is 30 hours. Do the following:
- 1) Estimate the parameters of the Crow Extended model.
- 2) What is the projected MTBF and growth potential?
- 3) Under the current management strategy, is it even possible to reach the MTBF goal of 30 hours?
| Table 9.10 - Multiple Systems (Known Operating Times) data for Example 10 | ||||
| Failed Unit ID | Time Unit 1 | Time Unit 2 | Classification | Mode |
|---|---|---|---|---|
| 1 | 16.5 | 0 | BD | seal leak |
| 1 | 16.5 | 0 | BD | valve |
| 1 | 17 | 0 | A | |
| 2 | 20.5 | 0.9 | A | |
| 2 | 25.3 | 3.8 | BD | hose |
| 2 | 28.7 | 4.6 | BD | operator error |
| 1 | 41.8 | 14.7 | BD | bearing |
| 1 | 45.5 | 17.6 | A | |
| 2 | 48.6 | 22 | A | |
| 2 | 49.6 | 23.4 | BD | seal leak |
| 1 | 51.4 | 26.3 | A | |
| 1 | 58.2 | 35.7 | BD | seal leak |
| 2 | 59 | 36.5 | A | |
| 2 | 60.6 | 37.6 | BD | hose |
| 1 | 61.9 | 39.1 | BD | seal leak |
| 1 | 76.6 | 55.4 | BD | bearing |
| 2 | 81.1 | 61.1 | A | |
| 1 | 84.1 | 63.6 | A | |
| 1 | 84.7 | 64.3 | A | |
| 1 | 94.6 | 72.6 | A | |
| 2 | 100 | 78.1 | BD | valve |
| 1 | 104 | 81.4 | BD | bearing |
| 2 | 104.8 | 85.9 | BD | spring |
| 2 | 105.9 | 87.1 | BD | operator error |
| 1 | 108.8 | 89.9 | BD | hose |
| 2 | 132.4 | 119.5 | BD | spring |
| 2 | 132.4 | 150.1 | BD | operator error |
| 2 | 132.4 | 153.7 | A | |
Solution to Example 10
- 1) Figure CrowExtend9 shows the estimated Crow Extended parameters.
- 2) One possible method to calculate the projected MTBF and growth potential is to use the Quick Calculation Pad, but you can also view these two values at the same time by viewing the Growth Potential MTBF plot, which is displayed in Figure CrowExtend10. From the plot, the projected MTBF is equal to 16.87 hours and the growth potential is equal to 18.63 hours.
- 3) The current projected MTBF and growth potential MTBF are both well below the required goal of 30 hours. To check if this goal can even be reached, you can set the effectiveness factor equal to 1. In other words, if all of the corrective actions were to remove the failure modes completely then what would be the projected and growth potential MTBF? After changing the fixed effectiveness factor to 1, the parameters are recalculated and the Growth Potential plot is refreshed. The refreshed plot is shown in Figure CrowExtend11. Even if you assume an effectiveness factor equal to 1, the growth potential is still only 27.27 hours. Based on the current design process, it will not be possible to reach the MTBF goal of 30 hours. Therefore, there are basically two options: start a new design stage or reduce the required MTBF goal.
[math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math]