Inverse Power Law (IPL)-Lognormal Model: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(23 intermediate revisions by 2 users not shown)
Line 1: Line 1:
{{Reference Example|ALTA_Reference_Examples_Banner.png|ALTA_Reference_Examples}}
{{Reference Example|{{Banner ALTA Reference Examples}}}}


This example validates the IPL life stress relationship with a lognormal distribution.
This example validates the calculations for the IPL life stress relationship with a lognormal distribution in ALTA standard folios.




Line 11: Line 11:
{{Reference_Example_Heading2}}
{{Reference_Example_Heading2}}


A Mylar-Polyurethane Insulating structure was tested under several different voltage settings. The test data is given in the table shown next.
A Mylar-Polyurethane insulating structure was tested under several different voltage settings. The following table shows the test data.


{| {{table}}
{| {{table}}
Line 94: Line 94:
{{Reference_Example_Heading3}}
{{Reference_Example_Heading3}}


The following function is used for the Ln-Mean :
The following function is used for the Ln-Mean <math>\,\!\mu {}'</math>:


::<math>\,\!</math>


where V is the voltage and its natural log transform is used in the above life stress relation.  
::<math>\,\!\mu {}'=\beta _{0}+\beta _{1}\times log\left ( V \right )</math>
 
 
where ''V'' is the voltage and its natural log transform is used in the above life stress relation.  
 


This function can be written in the following way:
This function can be written in the following way:


::<math>\,\!</math>


The above equation is the general log-linear model in ALTA. In ALTA, the coefficients are denoted by .
::<math>\,\!e^{\mu {}'}=e^{\alpha _{0}+\alpha _{1}log\left ( V \right )}</math>
 
 
The above equation is the general log-linear model in ALTA. In ALTA, the coefficients are denoted by <math>\,\!\alpha _{i}</math>.
 


In fact, the above model also can be expressed using the traditional IPL (inverse power law) model:
In fact, the above model also can be expressed using the traditional IPL (inverse power law) model:


::<math>\,\!</math>
 
::<math>\,\!e^{\mu {}'}=\frac{1}{K\cdot V^{n}}</math>
 
   
   
where <math>\,\!</math>  and <math>\,\!</math> .  
where <math>\,\!K=e^{-\alpha _{0}}</math>  and <math>\,\!n=-\alpha _{1}</math>.  




In the book, the following results are provided:
In the book, the following results are provided:


*ML estimations for the model parameters are: <math>\,\!</math> , <math>\,\!</math> and <math>\,\!</math> .
*ML estimations for the model parameters are: <math>\,\!\sigma =1.05</math> , <math>\,\!\beta _{0}=27.5</math> and <math>\,\!\beta _{1}=-4.29</math>.
*The standard deviation of each parameter are: <math>\,\!</math> , <math>\,\!</math> and <math>\,\!</math> . Therefore, their variances are: <math>\,\!</math> , <math>\,\!</math> , <math>\,\!</math> .  
 
 
*The standard deviation of each parameter are: <math>\,\!std\left ( \sigma  \right )=0.12</math> , <math>\,\!std\left ( \beta _{0}  \right )=3.0</math> and <math>\,\!std\left ( \beta _{1}  \right )=0.6</math>.  
 
:Therefore, their variances are: <math>\,\!Var\left ( \sigma  \right )=0.0144</math> , <math>\,\!Var\left ( \beta _{0}  \right )=9</math> and <math>\,\!Var\left ( \beta _{1}  \right )=0.36</math>.  
 
*The log-likelihood value is -271.4.
*The log-likelihood value is -271.4.
*The 95% two-sided confidence intervals are: for <math>\,\!</math> , it is [0.83, 1.32]; for <math>\,\!</math> it is [21.6, 33.4]; for <math>\,\!</math> , <math>\,\!</math> it is [-5.46, -3.11].
 
 
*The 95% two-sided confidence intervals are: for <math>\,\!\sigma</math> , it is [0.83, 1.32]; for <math>\,\!\beta _{0}</math> , it is [21.6, 33.4]; and for <math>\,\!\beta _{1}</math> , it is [-5.46, -3.11].
 




{{Reference_Example_Heading4|ALTA}}
{{Reference_Example_Heading4|ALTA}}
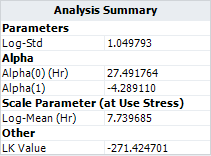
*ML estimations for the model parameters are:
[[image:IPL Lognormal_Analysis Summary.png|center]]
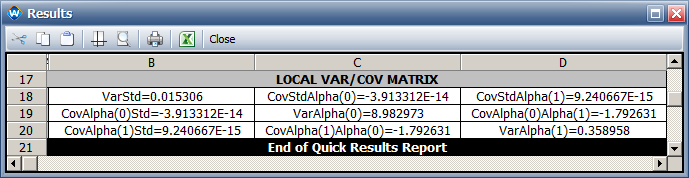
*The variance and covariance matrix for model parameters is:
[[image:IPL Lognormal_Var_Cov Results.png|center]]
*The log-likelihood value is -271.4247.
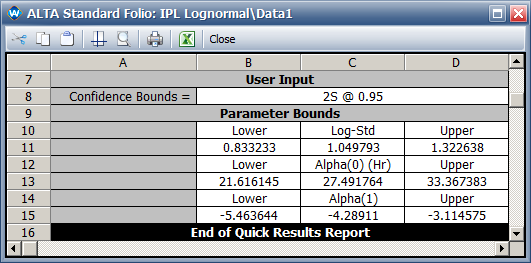
*The 95% two-sided confidence intervals are:
[[image:IPL Lognormal_Parameter Bounds.png|center]]

Latest revision as of 18:19, 28 September 2015

ALTA Reference Examples Banner.png


New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.



Inverse Power Law (IPL)-Lognormal Model

This example validates the calculations for the IPL life stress relationship with a lognormal distribution in ALTA standard folios.


Reference Case

The data set is from Example 19.10 on page 504 in book Statistical Methods for Reliability Data by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998.


Data

A Mylar-Polyurethane insulating structure was tested under several different voltage settings. The following table shows the test data.

Time Failed (Hr) Voltage (kV)
15 219
16 219
36 219
50 219
55 219
95 219
122 219
129 219
625 219
700 219
49 157.1
99 157.1
154.5 157.1
180 157.1
291 157.1
447 157.1
510 157.1
600 157.1
1656 157.1
1721 157.1
188 122.4
297 122.4
405 122.4
744 122.4
1218 122.4
1340 122.4
1715 122.4
3382 122.4
606 100.3
1012 100.3
2520 100.3
2610 100.3
3988 100.3
4100 100.3
5025 100.3
6842 100.3


Result

The following function is used for the Ln-Mean [math]\displaystyle{ \,\!\mu {}' }[/math]:


[math]\displaystyle{ \,\!\mu {}'=\beta _{0}+\beta _{1}\times log\left ( V \right ) }[/math]


where V is the voltage and its natural log transform is used in the above life stress relation.


This function can be written in the following way:


[math]\displaystyle{ \,\!e^{\mu {}'}=e^{\alpha _{0}+\alpha _{1}log\left ( V \right )} }[/math]


The above equation is the general log-linear model in ALTA. In ALTA, the coefficients are denoted by [math]\displaystyle{ \,\!\alpha _{i} }[/math].


In fact, the above model also can be expressed using the traditional IPL (inverse power law) model:


[math]\displaystyle{ \,\!e^{\mu {}'}=\frac{1}{K\cdot V^{n}} }[/math]


where [math]\displaystyle{ \,\!K=e^{-\alpha _{0}} }[/math] and [math]\displaystyle{ \,\!n=-\alpha _{1} }[/math].


In the book, the following results are provided:

  • ML estimations for the model parameters are: [math]\displaystyle{ \,\!\sigma =1.05 }[/math] , [math]\displaystyle{ \,\!\beta _{0}=27.5 }[/math] and [math]\displaystyle{ \,\!\beta _{1}=-4.29 }[/math].


  • The standard deviation of each parameter are: [math]\displaystyle{ \,\!std\left ( \sigma \right )=0.12 }[/math] , [math]\displaystyle{ \,\!std\left ( \beta _{0} \right )=3.0 }[/math] and [math]\displaystyle{ \,\!std\left ( \beta _{1} \right )=0.6 }[/math].
Therefore, their variances are: [math]\displaystyle{ \,\!Var\left ( \sigma \right )=0.0144 }[/math] , [math]\displaystyle{ \,\!Var\left ( \beta _{0} \right )=9 }[/math] and [math]\displaystyle{ \,\!Var\left ( \beta _{1} \right )=0.36 }[/math].


  • The log-likelihood value is -271.4.


  • The 95% two-sided confidence intervals are: for [math]\displaystyle{ \,\!\sigma }[/math] , it is [0.83, 1.32]; for [math]\displaystyle{ \,\!\beta _{0} }[/math] , it is [21.6, 33.4]; and for [math]\displaystyle{ \,\!\beta _{1} }[/math] , it is [-5.46, -3.11].


Results in ALTA

  • ML estimations for the model parameters are:
IPL Lognormal Analysis Summary.png


  • The variance and covariance matrix for model parameters is:
IPL Lognormal Var Cov Results.png


  • The log-likelihood value is -271.4247.


  • The 95% two-sided confidence intervals are:
IPL Lognormal Parameter Bounds.png
Retrieved from "https://www.reliawiki.com/index.php?title=Inverse_Power_Law_(IPL)-Lognormal_Model&oldid=60831"