Test-Find-Test Data Example: Difference between revisions
No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| (8 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner RGA Examples}} | <noinclude>{{Banner RGA Examples}} | ||
''This example appears in the [ | ''This example appears in the [https://help.reliasoft.com/reference/reliability_growth_and_repairable_system_analysis Reliability growth reference]''. | ||
</noinclude> | </noinclude> | ||
Consider the data in the first table below. A system was tested for <math>T=400\,\!</math> hours. There were a total of <math>N=42\,\!</math> failures and all corrective actions will be delayed until after the end of the 400 hour test. Each failure has been designated as either an A failure mode (the cause will not receive a corrective action) or a BD mode (the cause will receive a corrective action). There are <math>{{N}_{A}}=10\,\!</math> A mode failures and <math>{{N}_{BD}}=32\,\!</math> BD mode failures. In addition, there are <math>M=16\,\!</math> distinct BD failure modes, which means 16 distinct corrective actions will be incorporated into the system at the end of test. The total number of failures for the <math>{{j}^{th}}\,\!</math> observed distinct BD mode is denoted by <math>{{N}_{j}}\,\!</math>, and the total number of BD failures during the test is <math>{{N}_{BD}}=\underset{j=1}{\overset{M}{\mathop{\sum }}}\,{{N}_{j}}\,\!</math>. These values and effectiveness factors are given in the second table | Consider the data in the first table below. A system was tested for <math>T=400\,\!</math> hours. There were a total of <math>N=42\,\!</math> failures and all corrective actions will be delayed until after the end of the 400 hour test. Each failure has been designated as either an A failure mode (the cause will not receive a corrective action) or a BD mode (the cause will receive a corrective action). There are <math>{{N}_{A}}=10\,\!</math> A mode failures and <math>{{N}_{BD}}=32\,\!</math> BD mode failures. In addition, there are <math>M=16\,\!</math> distinct BD failure modes, which means 16 distinct corrective actions will be incorporated into the system at the end of test. The total number of failures for the <math>{{j}^{th}}\,\!</math> observed distinct BD mode is denoted by <math>{{N}_{j}}\,\!</math>, and the total number of BD failures during the test is <math>{{N}_{BD}}=\underset{j=1}{\overset{M}{\mathop{\sum }}}\,{{N}_{j}}\,\!</math>. These values and effectiveness factors are given in the second table | ||
Do the following: | Do the following: | ||
#Determine the projected MTBF and failure intensity. | |||
#Determine the growth potential MTBF and failure intensity. | |||
#Determine the demonstrated MTBF and failure intensity. | |||
<div style="margin-left:auto; margin-right: auto; width: 590px;"> | |||
<div style="float: left;"> | |||
<div style="width: | |||
{|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | {|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | ||
|- | |- | ||
| Line 71: | Line 70: | ||
</div> | </div> | ||
<div style=" | <div style="float: right;"> | ||
{|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | {|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | ||
|- | |- | ||
| Line 113: | Line 112: | ||
|16|| 1|| 395.2|| .46 | |16|| 1|| 395.2|| .46 | ||
|} | |} | ||
</div> | |||
</div> | </div> | ||
<p style="clear: both;"></p> | <p style="clear: both;"></p> | ||
| Line 118: | Line 118: | ||
'''Solution''' | '''Solution''' | ||
<ol> | |||
<li>The maximum likelihood estimates of <math>{{\beta }_{BD}}\,\!</math> and <math>{{\lambda }_{BD}}\,\!</math> are determined to be: | |||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 144: | Line 145: | ||
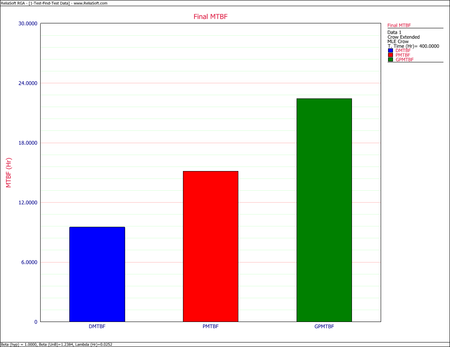
:<math>M\widehat{T}B{{F}_{P}}={{[r(T)]}^{-1}}=15.127\,\!</math> | :<math>M\widehat{T}B{{F}_{P}}={{[r(T)]}^{-1}}=15.127\,\!</math> | ||
</li> | |||
<li>To estimate the maximum reliability that can be attained with this management strategy, use the following calculations. | |||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 163: | Line 165: | ||
:<math>M\widehat{T}B{{F}_{GP}}={{[{{\widehat{r}}_{GP}}]}^{-1}}=22.4467\,\!</math> | :<math>M\widehat{T}B{{F}_{GP}}={{[{{\widehat{r}}_{GP}}]}^{-1}}=22.4467\,\!</math> | ||
</li> | |||
<li>The demonstrated failure intensity and MTBF are estimated by: | |||
:<math>\begin{align} | :<math>\begin{align} | ||
{{\widehat{\lambda }}_{D}}(T) = & \frac{{{N}_{A}}+{{N}_{BD}}}{T} \\ | {{\widehat{\lambda }}_{D}}(T) = & \frac{{{N}_{A}}+{{N}_{BD}}}{T} \\ | ||
| Line 179: | Line 182: | ||
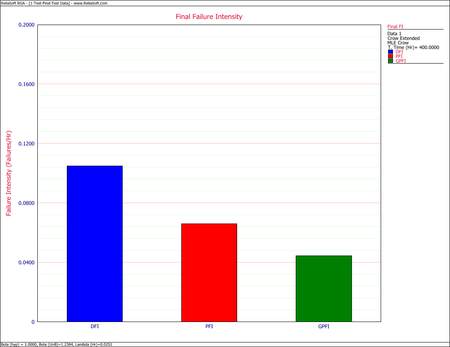
The first chart below shows the demonstrated, projected and growth potential MTBF. The second shows the demonstrated, projected and growth potential failure intensity. | The first chart below shows the demonstrated, projected and growth potential MTBF. The second shows the demonstrated, projected and growth potential failure intensity. | ||
[[Image:rga9.3.png|center| | [[Image:rga9.3.png|center|450px]] | ||
[[Image:rga9.4.png|center| | [[Image:rga9.4.png|center|450px]] | ||
</li> | |||
</ol> | |||
Latest revision as of 21:30, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability growth reference.
Consider the data in the first table below. A system was tested for [math]\displaystyle{ T=400\,\! }[/math] hours. There were a total of [math]\displaystyle{ N=42\,\! }[/math] failures and all corrective actions will be delayed until after the end of the 400 hour test. Each failure has been designated as either an A failure mode (the cause will not receive a corrective action) or a BD mode (the cause will receive a corrective action). There are [math]\displaystyle{ {{N}_{A}}=10\,\! }[/math] A mode failures and [math]\displaystyle{ {{N}_{BD}}=32\,\! }[/math] BD mode failures. In addition, there are [math]\displaystyle{ M=16\,\! }[/math] distinct BD failure modes, which means 16 distinct corrective actions will be incorporated into the system at the end of test. The total number of failures for the [math]\displaystyle{ {{j}^{th}}\,\! }[/math] observed distinct BD mode is denoted by [math]\displaystyle{ {{N}_{j}}\,\! }[/math], and the total number of BD failures during the test is [math]\displaystyle{ {{N}_{BD}}=\underset{j=1}{\overset{M}{\mathop{\sum }}}\,{{N}_{j}}\,\! }[/math]. These values and effectiveness factors are given in the second table
Do the following:
- Determine the projected MTBF and failure intensity.
- Determine the growth potential MTBF and failure intensity.
- Determine the demonstrated MTBF and failure intensity.
| Test-Find-Test Data | ||||||
| [math]\displaystyle{ i\,\! }[/math] | [math]\displaystyle{ {{X}_{i}}\,\! }[/math] | Mode | [math]\displaystyle{ i\,\! }[/math] | [math]\displaystyle{ {{X}_{i}}\,\! }[/math] | Mode | |
|---|---|---|---|---|---|---|
| 1 | 15 | BD1 | 22 | 260.1 | BD1 | |
| 2 | 25.3 | BD2 | 23 | 263.5 | BD8 | |
| 3 | 47.5 | BD3 | 24 | 273.1 | A | |
| 4 | 54 | BD4 | 25 | 274.7 | BD6 | |
| 5 | 56.4 | BD5 | 26 | 285 | BD13 | |
| 6 | 63.6 | A | 27 | 304 | BD9 | |
| 7 | 72.2 | BD5 | 28 | 315.4 | BD4 | |
| 8 | 99.6 | BD6 | 29 | 317.1 | A | |
| 9 | 100.3 | BD7 | 30 | 320.6 | A | |
| 10 | 102.5 | A | 31 | 324.5 | BD12 | |
| 11 | 112 | BD8 | 32 | 324.9 | BD10 | |
| 12 | 120.9 | BD2 | 33 | 342 | BD5 | |
| 13 | 125.5 | BD9 | 34 | 350.2 | BD3 | |
| 14 | 133.4 | BD10 | 35 | 364.6 | BD10 | |
| 15 | 164.7 | BD9 | 36 | 364.9 | A | |
| 16 | 177.4 | BD10 | 37 | 366.3 | BD2 | |
| 17 | 192.7 | BD11 | 38 | 373 | BD8 | |
| 18 | 213 | A | 39 | 379.4 | BD14 | |
| 19 | 244.8 | A | 40 | 389 | BD15 | |
| 20 | 249 | BD12 | 41 | 394.9 | A | |
| 21 | 250.8 | A | 42 | 395.2 | BD16 | |
| Effectiveness Factors for the Unique BD Modes | |||
| BD Mode | Number [math]\displaystyle{ {{N}_{j}}\,\! }[/math] | First Occurrence | EF [math]\displaystyle{ {{d}_{i}}\,\! }[/math] |
|---|---|---|---|
| 1 | 2 | 15.0 | .67 |
| 2 | 3 | 25.3 | .72 |
| 3 | 2 | 47.5 | .77 |
| 4 | 2 | 54.0 | .77 |
| 5 | 3 | 54.0 | .87 |
| 6 | 2 | 99.6 | .92 |
| 7 | 1 | 100.3 | .50 |
| 8 | 3 | 112.0 | .85 |
| 9 | 3 | 125.5 | .89 |
| 10 | 4 | 133.4 | .74 |
| 11 | 1 | 192.7 | .70 |
| 12 | 2 | 249.0 | .63 |
| 13 | 1 | 285.0 | .64 |
| 14 | 1 | 379.4 | .72 |
| 15 | 1 | 389.0 | .69 |
| 16 | 1 | 395.2 | .46 |
Solution
- The maximum likelihood estimates of [math]\displaystyle{ {{\beta }_{BD}}\,\! }[/math] and [math]\displaystyle{ {{\lambda }_{BD}}\,\! }[/math] are determined to be:
- [math]\displaystyle{ \begin{align} {{{\hat{\beta }}}_{BD}} = & \frac{M}{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,\ln (\tfrac{T}{{{X}_{i}}})} \\ = & 0.7970 \\ {{{\hat{\lambda }}}_{BD}} = & 0.1350 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{\overline{\beta }}_{BD}} = & \frac{M-1}{M}{{{\hat{\beta }}}_{BD}} \\ = & 0.7472 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} r(T) = & \left( \frac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T} \right)+\overline{d}\left( \frac{M}{T}{{\overline{\beta }}_{BD}} \right) \\ = & 0.0661 \end{align}\,\! }[/math]
- [math]\displaystyle{ M\widehat{T}B{{F}_{P}}={{[r(T)]}^{-1}}=15.127\,\! }[/math]
- To estimate the maximum reliability that can be attained with this management strategy, use the following calculations.
- [math]\displaystyle{ \begin{align} {{N}_{A}}/T=0.0250 \end{align}\,\! }[/math]
- [math]\displaystyle{ \frac{1}{T}\underset{i=1}{\overset{16}{\mathop \sum }}\,(1-{{d}_{i}}){{N}_{i}}=0.0196\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{\widehat{r}}_{GP}}(T) = & \left( \frac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T} \right) \\ = & 0.0250+0.0196 \\ = & 0.0446 \end{align}\,\! }[/math]
- [math]\displaystyle{ M\widehat{T}B{{F}_{GP}}={{[{{\widehat{r}}_{GP}}]}^{-1}}=22.4467\,\! }[/math]
- The demonstrated failure intensity and MTBF are estimated by:
- [math]\displaystyle{ \begin{align} {{\widehat{\lambda }}_{D}}(T) = & \frac{{{N}_{A}}+{{N}_{BD}}}{T} \\ = & \frac{42}{400} \\ = & 0.1050 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} M\widehat{T}B{{F}_{D}} = & {{[{{\widehat{\lambda }}_{D}}(T)]}^{-1}} \\ = & 9.5238 \end{align}\,\! }[/math]