Test-Find-Test Data Example

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.

---

This example appears in the Reliability growth reference.

Consider the data in the first table below. A system was tested for [math]\displaystyle{ T=400\,\! }[/math] hours. There were a total of [math]\displaystyle{ N=42\,\! }[/math] failures and all corrective actions will be delayed until after the end of the 400 hour test. Each failure has been designated as either an A failure mode (the cause will not receive a corrective action) or a BD mode (the cause will receive a corrective action). There are [math]\displaystyle{ {{N}_{A}}=10\,\! }[/math] A mode failures and [math]\displaystyle{ {{N}_{BD}}=32\,\! }[/math] BD mode failures. In addition, there are [math]\displaystyle{ M=16\,\! }[/math] distinct BD failure modes, which means 16 distinct corrective actions will be incorporated into the system at the end of test. The total number of failures for the [math]\displaystyle{ {{j}^{th}}\,\! }[/math] observed distinct BD mode is denoted by [math]\displaystyle{ {{N}_{j}}\,\! }[/math], and the total number of BD failures during the test is [math]\displaystyle{ {{N}_{BD}}=\underset{j=1}{\overset{M}{\mathop{\sum }}}\,{{N}_{j}}\,\! }[/math]. These values and effectiveness factors are given in the second table

Do the following:

1. Determine the projected MTBF and failure intensity.
2. Determine the growth potential MTBF and failure intensity.
3. Determine the demonstrated MTBF and failure intensity.

Test-Find-Test Data
[math]\displaystyle{ i\,\! }[/math]	[math]\displaystyle{ {{X}_{i}}\,\! }[/math]	Mode		[math]\displaystyle{ i\,\! }[/math]	[math]\displaystyle{ {{X}_{i}}\,\! }[/math]	Mode
1	15	BD1		22	260.1	BD1
2	25.3	BD2		23	263.5	BD8
3	47.5	BD3		24	273.1	A
4	54	BD4		25	274.7	BD6
5	56.4	BD5		26	285	BD13
6	63.6	A		27	304	BD9
7	72.2	BD5		28	315.4	BD4
8	99.6	BD6		29	317.1	A
9	100.3	BD7		30	320.6	A
10	102.5	A		31	324.5	BD12
11	112	BD8		32	324.9	BD10
12	120.9	BD2		33	342	BD5
13	125.5	BD9		34	350.2	BD3
14	133.4	BD10		35	364.6	BD10
15	164.7	BD9		36	364.9	A
16	177.4	BD10		37	366.3	BD2
17	192.7	BD11		38	373	BD8
18	213	A		39	379.4	BD14
19	244.8	A		40	389	BD15
20	249	BD12		41	394.9	A
21	250.8	A		42	395.2	BD16

 

Effectiveness Factors for the Unique BD Modes
BD Mode	Number [math]\displaystyle{ {{N}_{j}}\,\! }[/math]	First Occurrence	EF [math]\displaystyle{ {{d}_{i}}\,\! }[/math]
1	2	15.0	.67
2	3	25.3	.72
3	2	47.5	.77
4	2	54.0	.77
5	3	54.0	.87
6	2	99.6	.92
7	1	100.3	.50
8	3	112.0	.85
9	3	125.5	.89
10	4	133.4	.74
11	1	192.7	.70
12	2	249.0	.63
13	1	285.0	.64
14	1	379.4	.72
15	1	389.0	.69
16	1	395.2	.46

Solution

1. The maximum likelihood estimates of [math]\displaystyle{ {{\beta }_{BD}}\,\! }[/math] and [math]\displaystyle{ {{\lambda }_{BD}}\,\! }[/math] are determined to be:

   [math]\displaystyle{ \begin{align} {{{\hat{\beta }}}_{BD}} = & \frac{M}{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,\ln (\tfrac{T}{{{X}_{i}}})} \\ = & 0.7970 \\ {{{\hat{\lambda }}}_{BD}} = & 0.1350 \end{align}\,\! }[/math]

   The unbiased estimate of [math]\displaystyle{ \beta \,\! }[/math] is:

   [math]\displaystyle{ \begin{align} {{\overline{\beta }}_{BD}} = & \frac{M-1}{M}{{{\hat{\beta }}}_{BD}} \\ = & 0.7472 \end{align}\,\! }[/math]

   Based on the test data, [math]\displaystyle{ \overline{d}=\tfrac{1}{M}\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{i}}= 0.72125\,\! }[/math]. Therefore, [math]\displaystyle{ B(T)=\overline{d}\tfrac{M{{\overline{\beta }}_{BD}}}{T}=0.0215\,\! }[/math]. The projected failure intensity due to incorporating the 16 corrective actions is:

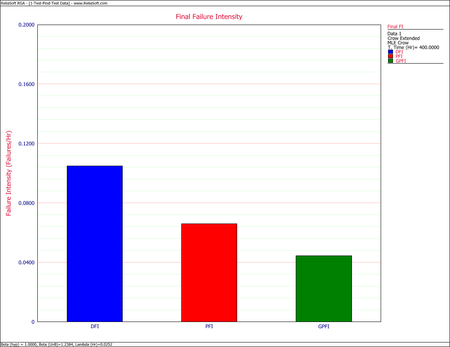
   [math]\displaystyle{ \begin{align} r(T) = & \left( \frac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T} \right)+\overline{d}\left( \frac{M}{T}{{\overline{\beta }}_{BD}} \right) \\ = & 0.0661 \end{align}\,\! }[/math]

   The projected MTBF is:

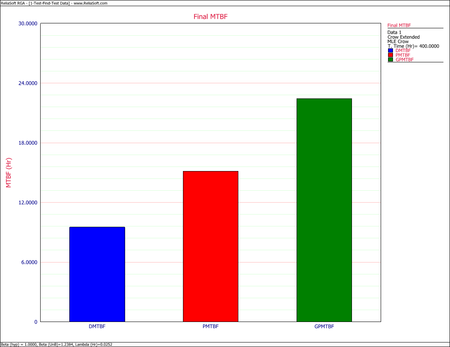
   [math]\displaystyle{ M\widehat{T}B{{F}_{P}}={{[r(T)]}^{-1}}=15.127\,\! }[/math]

2. To estimate the maximum reliability that can be attained with this management strategy, use the following calculations.

   [math]\displaystyle{ \begin{align} {{N}_{A}}/T=0.0250 \end{align}\,\! }[/math]

   [math]\displaystyle{ \frac{1}{T}\underset{i=1}{\overset{16}{\mathop \sum }}\,(1-{{d}_{i}}){{N}_{i}}=0.0196\,\! }[/math]

   The growth potential failure intensity is estimated by:

   [math]\displaystyle{ \begin{align} {{\widehat{r}}_{GP}}(T) = & \left( \frac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T} \right) \\ = & 0.0250+0.0196 \\ = & 0.0446 \end{align}\,\! }[/math]

   The growth potential MTBF is:

   [math]\displaystyle{ M\widehat{T}B{{F}_{GP}}={{[{{\widehat{r}}_{GP}}]}^{-1}}=22.4467\,\! }[/math]

3. The demonstrated failure intensity and MTBF are estimated by:

   [math]\displaystyle{ \begin{align} {{\widehat{\lambda }}_{D}}(T) = & \frac{{{N}_{A}}+{{N}_{BD}}}{T} \\ = & \frac{42}{400} \\ = & 0.1050 \end{align}\,\! }[/math]

   [math]\displaystyle{ \begin{align} M\widehat{T}B{{F}_{D}} = & {{[{{\widehat{\lambda }}_{D}}(T)]}^{-1}} \\ = & 9.5238 \end{align}\,\! }[/math]

   The first chart below shows the demonstrated, projected and growth potential MTBF. The second shows the demonstrated, projected and growth potential failure intensity.