Cumulative Damage Model for Progress Stress Profiles: Difference between revisions
Jump to navigation
Jump to search
Kate Racaza (talk | contribs) No edit summary |
Kate Racaza (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
{{Reference Example|ALTA_Reference_Examples_Banner.png|ALTA_Reference_Examples}} | {{Reference Example|ALTA_Reference_Examples_Banner.png|ALTA_Reference_Examples}} | ||
Compares the results | Compares the results of a cumulative damage model for a ramp stress test. | ||
{{Reference_Example_Heading1}} | {{Reference_Example_Heading1}} | ||
The data set is from the table on page 232 in the book ''Accelerated Testing: Statistical Models, Test Plans, and Data Analysis'' by Dr. Nelson, John Wiley & Sons, 1990. The model of Eqn. (3.10) is used and the results are given in Section 3 of Table 3.2 on page 511. | The data set is from the table on page 232 in the book ''Accelerated Testing: Statistical Models, Test Plans, and Data Analysis'' by Dr. Nelson, John Wiley & Sons, 1990. The model of Eqn. (3.10) is used and the results are given in Section 3 of Table 3.2 on page 511. | ||
{{Reference_Example_Heading2}} | {{Reference_Example_Heading2}} | ||
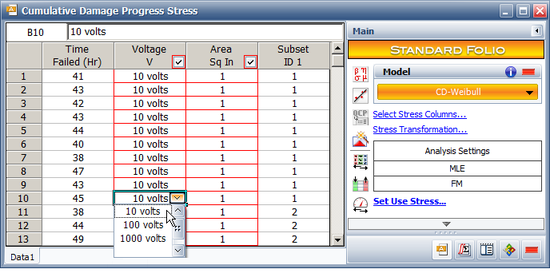
An accelerated test employed a pair of parallel disk electrodes immersed in insulating oil. The voltage ''V'' across the pair was increased linearly with time ''t'' at a specified rate, and then the voltage at oil breakdown was recorded. Since ''V = Rt'' (''R'' is the ramp rate), the time to breakdown can be recorded. The breakdown time is also affected by the two electrode areas ''A''. Three voltage linear rates and two electrode areas are used. The six stress profiles are: | |||
{| {{table}} | {| {{table}} | ||
| Line 299: | Line 300: | ||
{{Reference_Example_Heading3}} | {{Reference_Example_Heading3}} | ||
The following life stress relationship and Weibull distribution are used | The following life stress relationship and Weibull distribution are used to analyze the data. At a constant stress ''V'', the <math>\eta\,\!</math> is: | ||
::<math>ln(\eta(V, A)) = \alpha_{0}+\alpha_{1}ln(V)+\alpha_{2}ln(A)\,\!</math> | ::<math>ln\left(\eta(V, A)\right) = \alpha_{0}+\alpha_{1}ln(V)+\alpha_{2}ln(A)\,\!</math> | ||
| Line 311: | Line 312: | ||
When stress is varying with time, the reliability at time ''t'' is given as | When stress is varying with time, the reliability at time ''t'' is given as follows: | ||
::<math>R(t,V,A) = e^{-\left(\int_{0}^{t}\frac{1}{\eta(x,A)}dx\right)^\beta}</math> | ::<math>R(t,V,A) = e^{-\left(\int_{0}^{t}\frac{1}{\eta(x,A)}dx\right)^\beta}</math> | ||
| Line 329: | Line 330: | ||
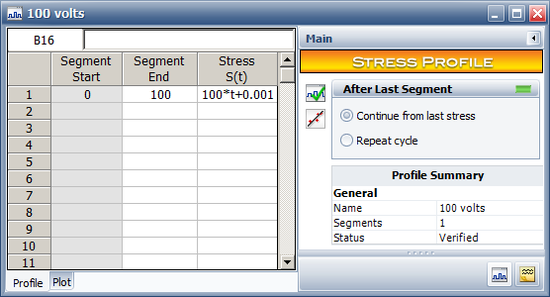
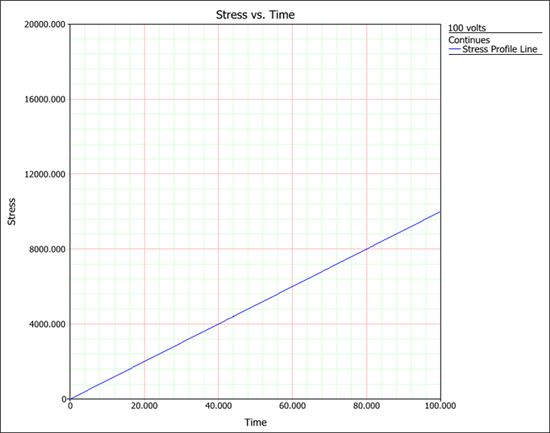
Note that the log transformation is used for voltage. At time 0, the voltage value will be 0 if the profile is defined as ''V(t) = 100*t''; therefore, to define this stress profile, we add a small number (i.e., 0.001)to the voltage function. | Note that the log transformation is used for voltage. At time 0, the voltage value will be 0 if the profile is defined as ''V(t) = 100*t''; therefore, to define this stress profile, we add a small number (i.e., 0.001) to the voltage function. | ||
The following picture shows the plot for this stress profile. | The following picture shows the plot for this stress profile. | ||
| Line 341: | Line 342: | ||
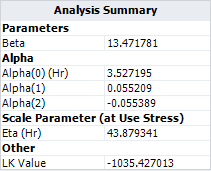
The log transformation is used for both stresses. The results in ALTA show that the calculated parameters are close to the results in the book, while the log likelihood value ( | The log transformation is used for both stresses. The results in ALTA show that the calculated parameters are close to the results in the book, while the log likelihood value (LK Value) is exactly the same as the value given in the book, as shown next. | ||
[[Image:Cum_Damage_Stress_Profile_result1.png|center]] | [[Image:Cum_Damage_Stress_Profile_result1.png|center]] | ||
Revision as of 23:19, 11 June 2014
ALTA_Reference_Examples_Banner.png