Crow Extended - Continuous Evaluation: Difference between revisions
Lisa Hacker (talk | contribs) No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 2: | Line 2: | ||
As discussed in the previous chapter, the [[Crow Extended|Crow Extended model]] is designed for a single test phase. However, in most cases testing for a system will be conducted in multiple phases. The Crow Extended - Continuous Evaluation model is designed for analyzing data across multiple test phases, while considering the data for all phases as one data set. In the RGA software, it is applied when using the Multi-Phase data sheet. | As discussed in the previous chapter, the [[Crow Extended|Crow Extended model]] is designed for a single test phase. However, in most cases testing for a system will be conducted in multiple phases. The Crow Extended - Continuous Evaluation model is designed for analyzing data across multiple test phases, while considering the data for all phases as one data set. In the RGA software, it is applied when using the Multi-Phase data sheet. | ||
<br> | <br> | ||
The Crow Extended - Continuous Evaluation (3-parameter) model is an extension of the Crow Extended model, and is designed for the practical testing situation where we need the flexibility to apply corrective actions at the time of failure or at a later time during the test, at the end of the current test or during a subsequent test phase. This three-parameter model is free of the constraint that testing must be stopped and all BD modes must be corrected at the end of the test, as in the Crow Extended model. The failure modes can be corrected during the test or when the testing is stopped for the incorporation of the fixes, or even not corrected at all at the end of the test phase. Based on this flexibility, the end time of testing is also not predefined, and it can be continuously updated with new test data, and this is the reason behind the naming, continuous evaluation. | The Crow Extended - Continuous Evaluation (3-parameter) model is an extension of the Crow Extended model, and is designed for the practical testing situation where we need the flexibility to apply corrective actions at the time of failure or at a later time during the test, at the end of the current test or during a subsequent test phase. This three-parameter model is free of the constraint that testing must be stopped and all BD modes must be corrected at the end of the test, as in the Crow Extended model. The failure modes can be corrected during the test or when the testing is stopped for the incorporation of the fixes, or even not corrected at all at the end of the test phase. Based on this flexibility, the end time of testing is also not predefined, and it can be continuously updated with new test data, and this is the reason behind the naming, continuous evaluation. | ||
Revision as of 00:40, 23 August 2012
As discussed in the previous chapter, the Crow Extended model is designed for a single test phase. However, in most cases testing for a system will be conducted in multiple phases. The Crow Extended - Continuous Evaluation model is designed for analyzing data across multiple test phases, while considering the data for all phases as one data set. In the RGA software, it is applied when using the Multi-Phase data sheet.
The Crow Extended - Continuous Evaluation (3-parameter) model is an extension of the Crow Extended model, and is designed for the practical testing situation where we need the flexibility to apply corrective actions at the time of failure or at a later time during the test, at the end of the current test or during a subsequent test phase. This three-parameter model is free of the constraint that testing must be stopped and all BD modes must be corrected at the end of the test, as in the Crow Extended model. The failure modes can be corrected during the test or when the testing is stopped for the incorporation of the fixes, or even not corrected at all at the end of the test phase. Based on this flexibility, the end time of testing is also not predefined, and it can be continuously updated with new test data, and this is the reason behind the naming, continuous evaluation.
Definitions
As discussed in the previous chapter, the Crow Extended model is designed for a single test phase. However, in most cases testing for a system will be conducted in multiple phases. The Crow Extended - Continuous Evaluation model is designed for analyzing data across multiple test phases, while considering the data for all phases as one data set. In the RGA software, it is applied when using the Multi-Phase data sheet.
The Crow Extended - Continuous Evaluation (3-parameter) model is an extension of the Crow Extended model, and is designed for the practical testing situation where we need the flexibility to apply corrective actions at the time of failure or at a later time during the test, at the end of the current test or during a subsequent test phase. This three-parameter model is free of the constraint that testing must be stopped and all BD modes must be corrected at the end of the test, as in the Crow Extended model. The failure modes can be corrected during the test or when the testing is stopped for the incorporation of the fixes, or even not corrected at all at the end of the test phase. Based on this flexibility, the end time of testing is also not predefined, and it can be continuously updated with new test data, and this is the reason behind the naming, continuous evaluation.
Definitions
Template loop detected: Template:Classifications crow rga Template loop detected: Template:Event codes crow rga
Template loop detected: Template:P ratio crow rga
Template loop detected: Template:Effectiveness factor crow rga
Template loop detected: Template:Growth potential and projections crow rga
Example 1
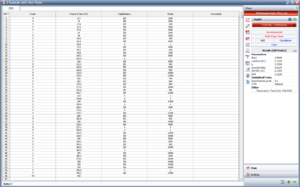
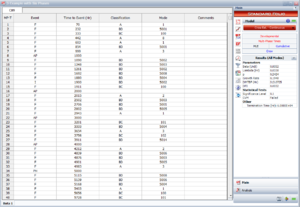
Table 10.2 shows the Multi-Phase data with failure and fix implementation events. Figure Example 1 data in RGA 7 shows the Table 10.2 data as entered in RGA 7. Note that since this is a time terminated test with a single phase ending at [math]\displaystyle{ T=400 }[/math] , the last event entry is a phase (PH) with time to event = 400.
| Table 10.2 - Multi-Phase data for a time terminated test at [math]\displaystyle{ T=400 }[/math] | ||||||||
| Event | Time to Event | Classification | Mode | Event | Time to Event | Classification | Mode | |
|---|---|---|---|---|---|---|---|---|
| F | 0.7 | BD | 1000 | F | 244.8 | A | 3 | |
| F | 15 | BD | 2000 | F | 249 | BD | 13000 | |
| F | 17.6 | BC | 200 | F | 250.8 | A | 2 | |
| F | 25.3 | BD | 3000 | F | 260.1 | BD | 2000 | |
| F | 47.5 | BD | 4000 | F | 273.1 | A | 5 | |
| I | 50 | BD | 1000 | F | 274.7 | BD | 11000 | |
| F | 54 | BD | 5000 | I | 280 | BD | 9000 | |
| F | 54.5 | BC | 300 | F | 282.8 | BC | 902 | |
| F | 56.4 | BD | 6000 | F | 285 | BD | 14000 | |
| F | 63.6 | A | 1 | F | 315.4 | BD | 4000 | |
| F | 72.2 | BD | 5000 | F | 317.1 | A | 3 | |
| F | 99.2 | BC | 400 | F | 320.6 | A | 1 | |
| F | 99.6 | BD | 7000 | F | 324.5 | BD | 12000 | |
| F | 100.3 | BD | 8000 | F | 324.9 | BD | 10000 | |
| F | 102.5 | A | 2 | F | 342 | BD | 5000 | |
| F | 112 | BD | 9000 | F | 350.2 | BD | 3000 | |
| F | 112.2 | BC | 500 | F | 355.2 | BC | 903 | |
| F | 120.9 | BD | 2000 | F | 364.6 | BD | 10000 | |
| F | 121.9 | BC | 600 | F | 364.9 | A | 1 | |
| F | 125.5 | BD | 10000 | I | 365 | BD | 10000 | |
| F | 133.4 | BD | 11000 | F | 366.3 | BD | 2000 | |
| F | 151 | BC | 700 | F | 379.4 | BD | 15000 | |
| F | 163 | BC | 800 | F | 389 | BD | 16000 | |
| F | 174.5 | BC | 900 | I | 390 | BD | 15000 | |
| F | 177.4 | BD | 10000 | I | 393 | BD | 16000 | |
| F | 191.6 | BC | 901 | F | 394.9 | A | 3 | |
| F | 192.7 | BD | 12000 | F | 395.2 | BD | 17000 | |
| F | 213 | A | 1 | |||||
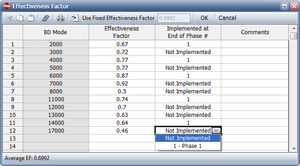
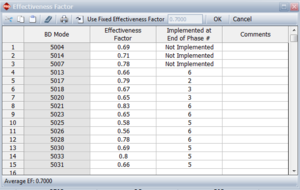
Figure EF example 1 shows the effectiveness factors for the unfixed BD modes and information concerning whether the fix will be implemented. Since we have only one test phase for this example, a 1 indicates that the fix will be implemented at the end of the first (and only) phase.
Do the following:
- 1) Determine the current demonstrated MTBF and failure intensity at time [math]\displaystyle{ T }[/math] .
- 2) Determine the nominal and actual average effectiveness factor at time [math]\displaystyle{ T }[/math] .
- 3) Determine the ratio.
- 4) Determine the nominal and actual growth potential factor.
- 5) Determine the unfixed BD mode failure intensity at time [math]\displaystyle{ T. }[/math]
- 6) Determine the rate of discovery parameters and the rate of discovery function at time [math]\displaystyle{ T }[/math] .
- 7) Determine the nominal growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 8) Determine the nominal projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 9) Determine the actual growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 10) Determine the actual projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
Solution
- 1) As seen in Chapter 5, for a time terminated test, [math]\displaystyle{ \beta }[/math] is estimated by the following equation:
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
where in this case [math]\displaystyle{ {{T}^{*}}= }[/math] termination time [math]\displaystyle{ =400, }[/math] and [math]\displaystyle{ n }[/math] is the total number of failures. In this example [math]\displaystyle{ n=50 }[/math] . Note that there are five fix implementation events and one event that marks the end of the phase. These should not be counted as failures.
So in this case we find that [math]\displaystyle{ \beta =0.9866. }[/math]
Note that here we calculated the biased estimate of [math]\displaystyle{ \beta }[/math] but we could have used the unbiased estimate as presented in Chapter 5. The choice of calculating the biased or unbiased estimate of [math]\displaystyle{ \beta }[/math] can be set in the User Setup in RGA 7.
Then solve for [math]\displaystyle{ \lambda , }[/math] based on the Crow-AMSAA (NHPP) equation explained in Chapter 5, Section 5.1.1:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{n}{{{T}^{*\beta }}} \\ & = & \frac{50}{{{400}^{0.9866}}} \\ & = & 0.1354 \end{align} }[/math]
The demonstrated MTBF of the system at time [math]\displaystyle{ T=400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{D}}= & \frac{1}{\lambda \beta {{T}^{\beta -1}}} \\ & = & 8.1087 \end{align} }[/math]
The corresponding current demonstrated failure intensity is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{D}}= & \frac{1}{MTB{{F}_{D}}} \\ & = & 0.1233 \end{align} }[/math]
- 2) The average nominal effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average Nominal EF):
- [math]\displaystyle{ \begin{align} & {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ & = & \frac{0.67+0.72+0.77+0.77+0.87+0.92+0.5+0.74+0.7+0.63+0.64+0.46}{12} \\ & = & 0.6992 \end{align} }[/math]
The average actual effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average actual EF):
- [math]\displaystyle{ \begin{align} & {{d}_{A}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M} \\ & = & \frac{0.67+0+0.77+0+0.87+0+0+0.74+0+0+0.64+0}{12} \\ & = & 0.3075 \end{align} }[/math]
- 3) The [math]\displaystyle{ p }[/math] ratio is calculated by using Eqn. (p ratio):
- [math]\displaystyle{ \begin{align} & p= & \frac{\text{Total number of distinct unfixed BD modes at time }400}{\text{Total number of distinct BD modes at time }400\text{ (both fixed and unfixed)}} \\ & = & \frac{12}{12+5} \\ & = & 0.7059 \end{align} }[/math]
- 4) The nominal growth potential factor is given by Eqn. (Nonimal GP Factor) :
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ni}} \right)\frac{{{N}_{i}}}{T} }[/math]
The total number [math]\displaystyle{ M }[/math] of distinct unfixed BD modes at time [math]\displaystyle{ 400 }[/math] is [math]\displaystyle{ M=12. }[/math]
- [math]\displaystyle{ {{d}_{Ni}} }[/math] is the assigned (nominal) EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}}, }[/math] (as given in Figure EF example 1).
- [math]\displaystyle{ {{N}_{i}} }[/math] is the total number of failures over (0, [math]\displaystyle{ 400 }[/math] ) for the distinct unfixed BD mode [math]\displaystyle{ i }[/math] . This is summarized in Table 10.3.
| Table 10.3 - Number of failures for unfixed BD modes | ||
| Classification | Mode | Number of Failures |
|---|---|---|
| BD | 2000 | 4 |
| BD | 3000 | 2 |
| BD | 4000 | 2 |
| BD | 5000 | 3 |
| BD | 6000 | 1 |
| BD | 7000 | 1 |
| BD | 8000 | 1 |
| BD | 11000 | 2 |
| BD | 12000 | 2 |
| BD | 13000 | 1 |
| BD | 14000 | 1 |
| BD | 17000 | 1 |
| Sum = 21 | ||
Based on the above, the nominal growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=0.0153 }[/math]
The actual growth potential factor is given by Eqn. (Actual GP factor):
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ai}} \right)\frac{{{N}_{i}}}{T} }[/math]
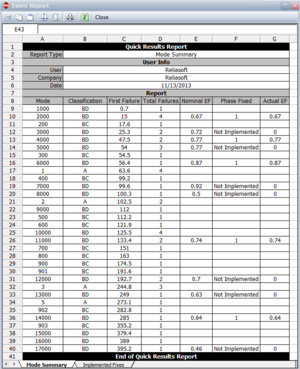
where [math]\displaystyle{ {{d}_{Ai}} }[/math] is the actual EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time 400, depending on whether a fix was implemented at time 400 or not. Figure Event report example 1 shows an event report from RGA 7 where it can be seen that the actual EF is zero if a fix was not implemented at 400, or equal to the nominal EF if the fix was implemented at 400.
Based on the above, the actual growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=0.0344 }[/math]
- 5) The total number of unfixed BD modes is 21, based on Table 10.2. From Eqn. (lambdaBDunfixed), the unfixed BD mode failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- 6) The discovery rate parameters at time [math]\displaystyle{ 400 }[/math] are calculated using all the first occurrences of all the BD modes, both fixed and unfixed. [math]\displaystyle{ {{\widehat{\beta }}_{BD}} }[/math] is the unbiased estimated of [math]\displaystyle{ \beta }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes in our example. [math]\displaystyle{ {{\widehat{\lambda }}_{BD}} }[/math] is the unbiased estimate of [math]\displaystyle{ \lambda }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the [math]\displaystyle{ 17 }[/math] distinct BD modes. Figure first occurence BD shows the first time to failure for each of the 17 distinct modes and the results of the analysis using the Crow-AMSAA (NHPP) model in RGA 7 (note that the calculation settings in the User Setup have to be set to calculate unbiased [math]\displaystyle{ \beta }[/math] in this case).
So we have:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6055 }[/math]
- and:
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.4518 }[/math]
The equations used to determine these parameters have been explained in question 1 of this example and are also presented in detail in Chapter 5, Section 5.1.1.
Based on Eqn. (Discovery Function), the discovery rate function at time 400 is:
- [math]\displaystyle{ \begin{align} & \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & 0.4518\cdot 0.6055\cdot {{400}^{0.6055-1}} \\ & = & 0.0257 \end{align} }[/math]
This is the failure intensity of the unseen BD modes at time 400. In this case, it means that 0.0257 new BD modes are discovered per hour, or one new BD mode is discovered every 38.9 hours.
Based on Eqn. (Nominal Growth Potential failure intensity), the nominal growth potential failure intensity is:
This is the minimum attainable failure intensity if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
From Eqn. (Nominal Growth Potential MTBF), the nominal growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NGP}}= & \frac{1}{{{\lambda }_{NGP}}} \\ & = & \frac{1}{0.080} \\ & = & 12.37 \end{align} }[/math]
This is the maximum attainable MTBF if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
- 8) From Eqn. (Nominal projected failure intensity), the nominal projected failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{NP}}= & {{\lambda }_{NGP}}+{{d}_{N}}h(400) \\ & = & 0.080+0.6992\cdot 0.0257 \\ & = & 0.0988 \end{align} }[/math]
This is the projected failure intensity assuming all delayed fixes have been implemented for the modes that have been seen.
The nominal projected MTBF at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NP}}= & \frac{1}{{{\lambda }_{NP}}} \\ & = & \frac{1}{0.0988} \\ & = & 10.11 \end{align} }[/math]
This is the projected MTBF assuming all delayed fixes have been implemented for the modes that have been seen.
- 9) Based on Eqn. (Actual GP FI), the actual growth potential failure intensity is:
This is the minimum attainable failure intensity based on the current management strategy.
The actual growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AGP}}= & \frac{1}{{{\lambda }_{AGP}}} \\ & = & \frac{1}{0.1029} \\ & = & 9.71 \end{align} }[/math]
This is the maximum attainable MTBF based on the current management strategy.
- 10) From Eqn. (Actual projected FI), the actual projected failure intensity at time is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{AP}}= & {{\lambda }_{AGP}}+{{d}_{A}}\cdot h\left( 400 \right) \\ & = & 0.1029+0.3075\cdot 0.0257 \\ & = & 0.1108 \end{align} }[/math]
This is the projected failure intensity based on the current management strategy.
The actual projected MTBF at time is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AP}}= & \frac{1}{{{\lambda }_{AP}}} \\ & = & \frac{1}{0.1108} \\ & = & 9.01 \end{align} }[/math]
This is the projected MTBF based on the current management strategy.
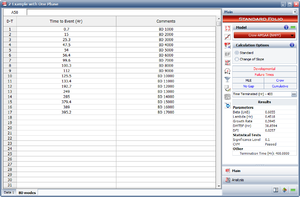
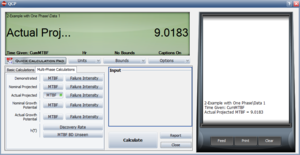
Figure QCP MTBFac demonstrates how we can derive the results of this example by using RGA 7's Quick Calculation Pad (QCP). Here we chose to calculate the actual projected MTBF.
Example 2
The Crow Extended - Continuous Evaluation model allows data analysis across multiple phases, up to seven individual phases. Figure Example2table, 6 phases shows a portion of failure time test results obtained across six phases. Analysis points are specified for continuous evaluation every 1000 hours. The cumulative test times at the end of each test phase are 5000, 15000, 25000, 35000, 45000 and 60000 hours.
Figure EFxample2 shows the effectiveness factors for the BD modes that do not have an associated fix implementation event. In other words, these are unfixed BD modes. Note that this specifies the phase after which the BD mode will be fixed, if any.
[math]\displaystyle{ }[/math]
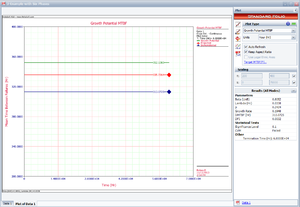
Figure Example2Plot shows the overall test results in terms of demonstrated, projected and growth potential MTBF.
[math]\displaystyle{ }[/math]
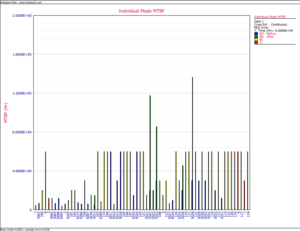
Figure Indivdual Mode MTBF shows the Before and After MTBFs for all the individual modes. Note that the After MTBFs are calculated by taking into account the respective effectiveness factors for each of the unfixed BD modes.
[math]\displaystyle{ }[/math]
The analysis points are used to track overall growth inside and across phases, at desired intervals. A multi-phase plot can be created by right-clicking Additional Plots in the Project Explorer and selecting Add MultiPhase Plot. The MultiPhase Plot Wizard guides you through the process concerning the data sheet selection. Since the Crow Extended - Continuous Evaluation was used for the six-phase test, we select the Multi-Phase option.
A Multi-Phase data sheet can be associated with the multi-phase plot. Also, if there is an existing Planning folio, the multi-phase plot can bring the test results together with the Planning. This allows you to track the overall reliability program against the goals and set plans at each stage of the test. Additional information on combining a Planning folio and a MultiPhase plot is presented in Chapter 11.
Figure Multi-phase plot shows the multi-phase plot for the six phases of the reliability growth test program. This plot can be a powerful tool for overall tracking of the reliability growth program. It displays the termination time for each phase of testing along with the demonstrated, projected and growth potential MTBFs at those times. The plot also displays these calculated MTBFs at specified analysis points, which are determined based on the "AP" events in the data sheet.
[math]\displaystyle{ }[/math]
Template loop detected: Template:Discrete data crow rga
Template loop detected: Template:Statistical tests for effectiveness of corrective actions crow rga
As discussed in the previous chapter, the Crow Extended model is designed for a single test phase. However, in most cases testing for a system will be conducted in multiple phases. The Crow Extended - Continuous Evaluation model is designed for analyzing data across multiple test phases, while considering the data for all phases as one data set. In the RGA software, it is applied when using the Multi-Phase data sheet.
The Crow Extended - Continuous Evaluation (3-parameter) model is an extension of the Crow Extended model, and is designed for the practical testing situation where we need the flexibility to apply corrective actions at the time of failure or at a later time during the test, at the end of the current test or during a subsequent test phase. This three-parameter model is free of the constraint that testing must be stopped and all BD modes must be corrected at the end of the test, as in the Crow Extended model. The failure modes can be corrected during the test or when the testing is stopped for the incorporation of the fixes, or even not corrected at all at the end of the test phase. Based on this flexibility, the end time of testing is also not predefined, and it can be continuously updated with new test data, and this is the reason behind the naming, continuous evaluation.
Definitions
Template loop detected: Template:Classifications crow rga Template loop detected: Template:Event codes crow rga
Template loop detected: Template:P ratio crow rga
Template loop detected: Template:Effectiveness factor crow rga
Template loop detected: Template:Growth potential and projections crow rga
Example 1
Table 10.2 shows the Multi-Phase data with failure and fix implementation events. Figure Example 1 data in RGA 7 shows the Table 10.2 data as entered in RGA 7. Note that since this is a time terminated test with a single phase ending at [math]\displaystyle{ T=400 }[/math] , the last event entry is a phase (PH) with time to event = 400.
| Table 10.2 - Multi-Phase data for a time terminated test at [math]\displaystyle{ T=400 }[/math] | ||||||||
| Event | Time to Event | Classification | Mode | Event | Time to Event | Classification | Mode | |
|---|---|---|---|---|---|---|---|---|
| F | 0.7 | BD | 1000 | F | 244.8 | A | 3 | |
| F | 15 | BD | 2000 | F | 249 | BD | 13000 | |
| F | 17.6 | BC | 200 | F | 250.8 | A | 2 | |
| F | 25.3 | BD | 3000 | F | 260.1 | BD | 2000 | |
| F | 47.5 | BD | 4000 | F | 273.1 | A | 5 | |
| I | 50 | BD | 1000 | F | 274.7 | BD | 11000 | |
| F | 54 | BD | 5000 | I | 280 | BD | 9000 | |
| F | 54.5 | BC | 300 | F | 282.8 | BC | 902 | |
| F | 56.4 | BD | 6000 | F | 285 | BD | 14000 | |
| F | 63.6 | A | 1 | F | 315.4 | BD | 4000 | |
| F | 72.2 | BD | 5000 | F | 317.1 | A | 3 | |
| F | 99.2 | BC | 400 | F | 320.6 | A | 1 | |
| F | 99.6 | BD | 7000 | F | 324.5 | BD | 12000 | |
| F | 100.3 | BD | 8000 | F | 324.9 | BD | 10000 | |
| F | 102.5 | A | 2 | F | 342 | BD | 5000 | |
| F | 112 | BD | 9000 | F | 350.2 | BD | 3000 | |
| F | 112.2 | BC | 500 | F | 355.2 | BC | 903 | |
| F | 120.9 | BD | 2000 | F | 364.6 | BD | 10000 | |
| F | 121.9 | BC | 600 | F | 364.9 | A | 1 | |
| F | 125.5 | BD | 10000 | I | 365 | BD | 10000 | |
| F | 133.4 | BD | 11000 | F | 366.3 | BD | 2000 | |
| F | 151 | BC | 700 | F | 379.4 | BD | 15000 | |
| F | 163 | BC | 800 | F | 389 | BD | 16000 | |
| F | 174.5 | BC | 900 | I | 390 | BD | 15000 | |
| F | 177.4 | BD | 10000 | I | 393 | BD | 16000 | |
| F | 191.6 | BC | 901 | F | 394.9 | A | 3 | |
| F | 192.7 | BD | 12000 | F | 395.2 | BD | 17000 | |
| F | 213 | A | 1 | |||||
Figure EF example 1 shows the effectiveness factors for the unfixed BD modes and information concerning whether the fix will be implemented. Since we have only one test phase for this example, a 1 indicates that the fix will be implemented at the end of the first (and only) phase.
Do the following:
- 1) Determine the current demonstrated MTBF and failure intensity at time [math]\displaystyle{ T }[/math] .
- 2) Determine the nominal and actual average effectiveness factor at time [math]\displaystyle{ T }[/math] .
- 3) Determine the ratio.
- 4) Determine the nominal and actual growth potential factor.
- 5) Determine the unfixed BD mode failure intensity at time [math]\displaystyle{ T. }[/math]
- 6) Determine the rate of discovery parameters and the rate of discovery function at time [math]\displaystyle{ T }[/math] .
- 7) Determine the nominal growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 8) Determine the nominal projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 9) Determine the actual growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 10) Determine the actual projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
Solution
- 1) As seen in Chapter 5, for a time terminated test, [math]\displaystyle{ \beta }[/math] is estimated by the following equation:
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
where in this case [math]\displaystyle{ {{T}^{*}}= }[/math] termination time [math]\displaystyle{ =400, }[/math] and [math]\displaystyle{ n }[/math] is the total number of failures. In this example [math]\displaystyle{ n=50 }[/math] . Note that there are five fix implementation events and one event that marks the end of the phase. These should not be counted as failures.
So in this case we find that [math]\displaystyle{ \beta =0.9866. }[/math]
Note that here we calculated the biased estimate of [math]\displaystyle{ \beta }[/math] but we could have used the unbiased estimate as presented in Chapter 5. The choice of calculating the biased or unbiased estimate of [math]\displaystyle{ \beta }[/math] can be set in the User Setup in RGA 7.
Then solve for [math]\displaystyle{ \lambda , }[/math] based on the Crow-AMSAA (NHPP) equation explained in Chapter 5, Section 5.1.1:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{n}{{{T}^{*\beta }}} \\ & = & \frac{50}{{{400}^{0.9866}}} \\ & = & 0.1354 \end{align} }[/math]
The demonstrated MTBF of the system at time [math]\displaystyle{ T=400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{D}}= & \frac{1}{\lambda \beta {{T}^{\beta -1}}} \\ & = & 8.1087 \end{align} }[/math]
The corresponding current demonstrated failure intensity is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{D}}= & \frac{1}{MTB{{F}_{D}}} \\ & = & 0.1233 \end{align} }[/math]
- 2) The average nominal effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average Nominal EF):
- [math]\displaystyle{ \begin{align} & {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ & = & \frac{0.67+0.72+0.77+0.77+0.87+0.92+0.5+0.74+0.7+0.63+0.64+0.46}{12} \\ & = & 0.6992 \end{align} }[/math]
The average actual effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average actual EF):
- [math]\displaystyle{ \begin{align} & {{d}_{A}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M} \\ & = & \frac{0.67+0+0.77+0+0.87+0+0+0.74+0+0+0.64+0}{12} \\ & = & 0.3075 \end{align} }[/math]
- 3) The [math]\displaystyle{ p }[/math] ratio is calculated by using Eqn. (p ratio):
- [math]\displaystyle{ \begin{align} & p= & \frac{\text{Total number of distinct unfixed BD modes at time }400}{\text{Total number of distinct BD modes at time }400\text{ (both fixed and unfixed)}} \\ & = & \frac{12}{12+5} \\ & = & 0.7059 \end{align} }[/math]
- 4) The nominal growth potential factor is given by Eqn. (Nonimal GP Factor) :
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ni}} \right)\frac{{{N}_{i}}}{T} }[/math]
The total number [math]\displaystyle{ M }[/math] of distinct unfixed BD modes at time [math]\displaystyle{ 400 }[/math] is [math]\displaystyle{ M=12. }[/math]
- [math]\displaystyle{ {{d}_{Ni}} }[/math] is the assigned (nominal) EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}}, }[/math] (as given in Figure EF example 1).
- [math]\displaystyle{ {{N}_{i}} }[/math] is the total number of failures over (0, [math]\displaystyle{ 400 }[/math] ) for the distinct unfixed BD mode [math]\displaystyle{ i }[/math] . This is summarized in Table 10.3.
| Table 10.3 - Number of failures for unfixed BD modes | ||
| Classification | Mode | Number of Failures |
|---|---|---|
| BD | 2000 | 4 |
| BD | 3000 | 2 |
| BD | 4000 | 2 |
| BD | 5000 | 3 |
| BD | 6000 | 1 |
| BD | 7000 | 1 |
| BD | 8000 | 1 |
| BD | 11000 | 2 |
| BD | 12000 | 2 |
| BD | 13000 | 1 |
| BD | 14000 | 1 |
| BD | 17000 | 1 |
| Sum = 21 | ||
Based on the above, the nominal growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=0.0153 }[/math]
The actual growth potential factor is given by Eqn. (Actual GP factor):
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ai}} \right)\frac{{{N}_{i}}}{T} }[/math]
where [math]\displaystyle{ {{d}_{Ai}} }[/math] is the actual EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time 400, depending on whether a fix was implemented at time 400 or not. Figure Event report example 1 shows an event report from RGA 7 where it can be seen that the actual EF is zero if a fix was not implemented at 400, or equal to the nominal EF if the fix was implemented at 400.
Based on the above, the actual growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=0.0344 }[/math]
- 5) The total number of unfixed BD modes is 21, based on Table 10.2. From Eqn. (lambdaBDunfixed), the unfixed BD mode failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- 6) The discovery rate parameters at time [math]\displaystyle{ 400 }[/math] are calculated using all the first occurrences of all the BD modes, both fixed and unfixed. [math]\displaystyle{ {{\widehat{\beta }}_{BD}} }[/math] is the unbiased estimated of [math]\displaystyle{ \beta }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes in our example. [math]\displaystyle{ {{\widehat{\lambda }}_{BD}} }[/math] is the unbiased estimate of [math]\displaystyle{ \lambda }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the [math]\displaystyle{ 17 }[/math] distinct BD modes. Figure first occurence BD shows the first time to failure for each of the 17 distinct modes and the results of the analysis using the Crow-AMSAA (NHPP) model in RGA 7 (note that the calculation settings in the User Setup have to be set to calculate unbiased [math]\displaystyle{ \beta }[/math] in this case).
So we have:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6055 }[/math]
- and:
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.4518 }[/math]
The equations used to determine these parameters have been explained in question 1 of this example and are also presented in detail in Chapter 5, Section 5.1.1.
Based on Eqn. (Discovery Function), the discovery rate function at time 400 is:
- [math]\displaystyle{ \begin{align} & \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & 0.4518\cdot 0.6055\cdot {{400}^{0.6055-1}} \\ & = & 0.0257 \end{align} }[/math]
This is the failure intensity of the unseen BD modes at time 400. In this case, it means that 0.0257 new BD modes are discovered per hour, or one new BD mode is discovered every 38.9 hours.
Based on Eqn. (Nominal Growth Potential failure intensity), the nominal growth potential failure intensity is:
This is the minimum attainable failure intensity if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
From Eqn. (Nominal Growth Potential MTBF), the nominal growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NGP}}= & \frac{1}{{{\lambda }_{NGP}}} \\ & = & \frac{1}{0.080} \\ & = & 12.37 \end{align} }[/math]
This is the maximum attainable MTBF if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
- 8) From Eqn. (Nominal projected failure intensity), the nominal projected failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{NP}}= & {{\lambda }_{NGP}}+{{d}_{N}}h(400) \\ & = & 0.080+0.6992\cdot 0.0257 \\ & = & 0.0988 \end{align} }[/math]
This is the projected failure intensity assuming all delayed fixes have been implemented for the modes that have been seen.
The nominal projected MTBF at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NP}}= & \frac{1}{{{\lambda }_{NP}}} \\ & = & \frac{1}{0.0988} \\ & = & 10.11 \end{align} }[/math]
This is the projected MTBF assuming all delayed fixes have been implemented for the modes that have been seen.
- 9) Based on Eqn. (Actual GP FI), the actual growth potential failure intensity is:
This is the minimum attainable failure intensity based on the current management strategy.
The actual growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AGP}}= & \frac{1}{{{\lambda }_{AGP}}} \\ & = & \frac{1}{0.1029} \\ & = & 9.71 \end{align} }[/math]
This is the maximum attainable MTBF based on the current management strategy.
- 10) From Eqn. (Actual projected FI), the actual projected failure intensity at time is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{AP}}= & {{\lambda }_{AGP}}+{{d}_{A}}\cdot h\left( 400 \right) \\ & = & 0.1029+0.3075\cdot 0.0257 \\ & = & 0.1108 \end{align} }[/math]
This is the projected failure intensity based on the current management strategy.
The actual projected MTBF at time is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AP}}= & \frac{1}{{{\lambda }_{AP}}} \\ & = & \frac{1}{0.1108} \\ & = & 9.01 \end{align} }[/math]
This is the projected MTBF based on the current management strategy.
Figure QCP MTBFac demonstrates how we can derive the results of this example by using RGA 7's Quick Calculation Pad (QCP). Here we chose to calculate the actual projected MTBF.
Example 2
The Crow Extended - Continuous Evaluation model allows data analysis across multiple phases, up to seven individual phases. Figure Example2table, 6 phases shows a portion of failure time test results obtained across six phases. Analysis points are specified for continuous evaluation every 1000 hours. The cumulative test times at the end of each test phase are 5000, 15000, 25000, 35000, 45000 and 60000 hours.
Figure EFxample2 shows the effectiveness factors for the BD modes that do not have an associated fix implementation event. In other words, these are unfixed BD modes. Note that this specifies the phase after which the BD mode will be fixed, if any.
[math]\displaystyle{ }[/math]
Figure Example2Plot shows the overall test results in terms of demonstrated, projected and growth potential MTBF.
[math]\displaystyle{ }[/math]
Figure Indivdual Mode MTBF shows the Before and After MTBFs for all the individual modes. Note that the After MTBFs are calculated by taking into account the respective effectiveness factors for each of the unfixed BD modes.
[math]\displaystyle{ }[/math]
The analysis points are used to track overall growth inside and across phases, at desired intervals. A multi-phase plot can be created by right-clicking Additional Plots in the Project Explorer and selecting Add MultiPhase Plot. The MultiPhase Plot Wizard guides you through the process concerning the data sheet selection. Since the Crow Extended - Continuous Evaluation was used for the six-phase test, we select the Multi-Phase option.
A Multi-Phase data sheet can be associated with the multi-phase plot. Also, if there is an existing Planning folio, the multi-phase plot can bring the test results together with the Planning. This allows you to track the overall reliability program against the goals and set plans at each stage of the test. Additional information on combining a Planning folio and a MultiPhase plot is presented in Chapter 11.
Figure Multi-phase plot shows the multi-phase plot for the six phases of the reliability growth test program. This plot can be a powerful tool for overall tracking of the reliability growth program. It displays the termination time for each phase of testing along with the demonstrated, projected and growth potential MTBFs at those times. The plot also displays these calculated MTBFs at specified analysis points, which are determined based on the "AP" events in the data sheet.
[math]\displaystyle{ }[/math]
Template loop detected: Template:Discrete data crow rga
Template loop detected: Template:Statistical tests for effectiveness of corrective actions crow rga
As discussed in the previous chapter, the Crow Extended model is designed for a single test phase. However, in most cases testing for a system will be conducted in multiple phases. The Crow Extended - Continuous Evaluation model is designed for analyzing data across multiple test phases, while considering the data for all phases as one data set. In the RGA software, it is applied when using the Multi-Phase data sheet.
The Crow Extended - Continuous Evaluation (3-parameter) model is an extension of the Crow Extended model, and is designed for the practical testing situation where we need the flexibility to apply corrective actions at the time of failure or at a later time during the test, at the end of the current test or during a subsequent test phase. This three-parameter model is free of the constraint that testing must be stopped and all BD modes must be corrected at the end of the test, as in the Crow Extended model. The failure modes can be corrected during the test or when the testing is stopped for the incorporation of the fixes, or even not corrected at all at the end of the test phase. Based on this flexibility, the end time of testing is also not predefined, and it can be continuously updated with new test data, and this is the reason behind the naming, continuous evaluation.
Definitions
Template loop detected: Template:Classifications crow rga Template loop detected: Template:Event codes crow rga
Template loop detected: Template:P ratio crow rga
Template loop detected: Template:Effectiveness factor crow rga
Template loop detected: Template:Growth potential and projections crow rga
Example 1
Table 10.2 shows the Multi-Phase data with failure and fix implementation events. Figure Example 1 data in RGA 7 shows the Table 10.2 data as entered in RGA 7. Note that since this is a time terminated test with a single phase ending at [math]\displaystyle{ T=400 }[/math] , the last event entry is a phase (PH) with time to event = 400.
| Table 10.2 - Multi-Phase data for a time terminated test at [math]\displaystyle{ T=400 }[/math] | ||||||||
| Event | Time to Event | Classification | Mode | Event | Time to Event | Classification | Mode | |
|---|---|---|---|---|---|---|---|---|
| F | 0.7 | BD | 1000 | F | 244.8 | A | 3 | |
| F | 15 | BD | 2000 | F | 249 | BD | 13000 | |
| F | 17.6 | BC | 200 | F | 250.8 | A | 2 | |
| F | 25.3 | BD | 3000 | F | 260.1 | BD | 2000 | |
| F | 47.5 | BD | 4000 | F | 273.1 | A | 5 | |
| I | 50 | BD | 1000 | F | 274.7 | BD | 11000 | |
| F | 54 | BD | 5000 | I | 280 | BD | 9000 | |
| F | 54.5 | BC | 300 | F | 282.8 | BC | 902 | |
| F | 56.4 | BD | 6000 | F | 285 | BD | 14000 | |
| F | 63.6 | A | 1 | F | 315.4 | BD | 4000 | |
| F | 72.2 | BD | 5000 | F | 317.1 | A | 3 | |
| F | 99.2 | BC | 400 | F | 320.6 | A | 1 | |
| F | 99.6 | BD | 7000 | F | 324.5 | BD | 12000 | |
| F | 100.3 | BD | 8000 | F | 324.9 | BD | 10000 | |
| F | 102.5 | A | 2 | F | 342 | BD | 5000 | |
| F | 112 | BD | 9000 | F | 350.2 | BD | 3000 | |
| F | 112.2 | BC | 500 | F | 355.2 | BC | 903 | |
| F | 120.9 | BD | 2000 | F | 364.6 | BD | 10000 | |
| F | 121.9 | BC | 600 | F | 364.9 | A | 1 | |
| F | 125.5 | BD | 10000 | I | 365 | BD | 10000 | |
| F | 133.4 | BD | 11000 | F | 366.3 | BD | 2000 | |
| F | 151 | BC | 700 | F | 379.4 | BD | 15000 | |
| F | 163 | BC | 800 | F | 389 | BD | 16000 | |
| F | 174.5 | BC | 900 | I | 390 | BD | 15000 | |
| F | 177.4 | BD | 10000 | I | 393 | BD | 16000 | |
| F | 191.6 | BC | 901 | F | 394.9 | A | 3 | |
| F | 192.7 | BD | 12000 | F | 395.2 | BD | 17000 | |
| F | 213 | A | 1 | |||||
Figure EF example 1 shows the effectiveness factors for the unfixed BD modes and information concerning whether the fix will be implemented. Since we have only one test phase for this example, a 1 indicates that the fix will be implemented at the end of the first (and only) phase.
Do the following:
- 1) Determine the current demonstrated MTBF and failure intensity at time [math]\displaystyle{ T }[/math] .
- 2) Determine the nominal and actual average effectiveness factor at time [math]\displaystyle{ T }[/math] .
- 3) Determine the ratio.
- 4) Determine the nominal and actual growth potential factor.
- 5) Determine the unfixed BD mode failure intensity at time [math]\displaystyle{ T. }[/math]
- 6) Determine the rate of discovery parameters and the rate of discovery function at time [math]\displaystyle{ T }[/math] .
- 7) Determine the nominal growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 8) Determine the nominal projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 9) Determine the actual growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 10) Determine the actual projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
Solution
- 1) As seen in Chapter 5, for a time terminated test, [math]\displaystyle{ \beta }[/math] is estimated by the following equation:
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
where in this case [math]\displaystyle{ {{T}^{*}}= }[/math] termination time [math]\displaystyle{ =400, }[/math] and [math]\displaystyle{ n }[/math] is the total number of failures. In this example [math]\displaystyle{ n=50 }[/math] . Note that there are five fix implementation events and one event that marks the end of the phase. These should not be counted as failures.
So in this case we find that [math]\displaystyle{ \beta =0.9866. }[/math]
Note that here we calculated the biased estimate of [math]\displaystyle{ \beta }[/math] but we could have used the unbiased estimate as presented in Chapter 5. The choice of calculating the biased or unbiased estimate of [math]\displaystyle{ \beta }[/math] can be set in the User Setup in RGA 7.
Then solve for [math]\displaystyle{ \lambda , }[/math] based on the Crow-AMSAA (NHPP) equation explained in Chapter 5, Section 5.1.1:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{n}{{{T}^{*\beta }}} \\ & = & \frac{50}{{{400}^{0.9866}}} \\ & = & 0.1354 \end{align} }[/math]
The demonstrated MTBF of the system at time [math]\displaystyle{ T=400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{D}}= & \frac{1}{\lambda \beta {{T}^{\beta -1}}} \\ & = & 8.1087 \end{align} }[/math]
The corresponding current demonstrated failure intensity is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{D}}= & \frac{1}{MTB{{F}_{D}}} \\ & = & 0.1233 \end{align} }[/math]
- 2) The average nominal effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average Nominal EF):
- [math]\displaystyle{ \begin{align} & {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ & = & \frac{0.67+0.72+0.77+0.77+0.87+0.92+0.5+0.74+0.7+0.63+0.64+0.46}{12} \\ & = & 0.6992 \end{align} }[/math]
The average actual effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average actual EF):
- [math]\displaystyle{ \begin{align} & {{d}_{A}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M} \\ & = & \frac{0.67+0+0.77+0+0.87+0+0+0.74+0+0+0.64+0}{12} \\ & = & 0.3075 \end{align} }[/math]
- 3) The [math]\displaystyle{ p }[/math] ratio is calculated by using Eqn. (p ratio):
- [math]\displaystyle{ \begin{align} & p= & \frac{\text{Total number of distinct unfixed BD modes at time }400}{\text{Total number of distinct BD modes at time }400\text{ (both fixed and unfixed)}} \\ & = & \frac{12}{12+5} \\ & = & 0.7059 \end{align} }[/math]
- 4) The nominal growth potential factor is given by Eqn. (Nonimal GP Factor) :
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ni}} \right)\frac{{{N}_{i}}}{T} }[/math]
The total number [math]\displaystyle{ M }[/math] of distinct unfixed BD modes at time [math]\displaystyle{ 400 }[/math] is [math]\displaystyle{ M=12. }[/math]
- [math]\displaystyle{ {{d}_{Ni}} }[/math] is the assigned (nominal) EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}}, }[/math] (as given in Figure EF example 1).
- [math]\displaystyle{ {{N}_{i}} }[/math] is the total number of failures over (0, [math]\displaystyle{ 400 }[/math] ) for the distinct unfixed BD mode [math]\displaystyle{ i }[/math] . This is summarized in Table 10.3.
| Table 10.3 - Number of failures for unfixed BD modes | ||
| Classification | Mode | Number of Failures |
|---|---|---|
| BD | 2000 | 4 |
| BD | 3000 | 2 |
| BD | 4000 | 2 |
| BD | 5000 | 3 |
| BD | 6000 | 1 |
| BD | 7000 | 1 |
| BD | 8000 | 1 |
| BD | 11000 | 2 |
| BD | 12000 | 2 |
| BD | 13000 | 1 |
| BD | 14000 | 1 |
| BD | 17000 | 1 |
| Sum = 21 | ||
Based on the above, the nominal growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=0.0153 }[/math]
The actual growth potential factor is given by Eqn. (Actual GP factor):
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ai}} \right)\frac{{{N}_{i}}}{T} }[/math]
where [math]\displaystyle{ {{d}_{Ai}} }[/math] is the actual EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time 400, depending on whether a fix was implemented at time 400 or not. Figure Event report example 1 shows an event report from RGA 7 where it can be seen that the actual EF is zero if a fix was not implemented at 400, or equal to the nominal EF if the fix was implemented at 400.
Based on the above, the actual growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=0.0344 }[/math]
- 5) The total number of unfixed BD modes is 21, based on Table 10.2. From Eqn. (lambdaBDunfixed), the unfixed BD mode failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- 6) The discovery rate parameters at time [math]\displaystyle{ 400 }[/math] are calculated using all the first occurrences of all the BD modes, both fixed and unfixed. [math]\displaystyle{ {{\widehat{\beta }}_{BD}} }[/math] is the unbiased estimated of [math]\displaystyle{ \beta }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes in our example. [math]\displaystyle{ {{\widehat{\lambda }}_{BD}} }[/math] is the unbiased estimate of [math]\displaystyle{ \lambda }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the [math]\displaystyle{ 17 }[/math] distinct BD modes. Figure first occurence BD shows the first time to failure for each of the 17 distinct modes and the results of the analysis using the Crow-AMSAA (NHPP) model in RGA 7 (note that the calculation settings in the User Setup have to be set to calculate unbiased [math]\displaystyle{ \beta }[/math] in this case).
So we have:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6055 }[/math]
- and:
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.4518 }[/math]
The equations used to determine these parameters have been explained in question 1 of this example and are also presented in detail in Chapter 5, Section 5.1.1.
Based on Eqn. (Discovery Function), the discovery rate function at time 400 is:
- [math]\displaystyle{ \begin{align} & \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & 0.4518\cdot 0.6055\cdot {{400}^{0.6055-1}} \\ & = & 0.0257 \end{align} }[/math]
This is the failure intensity of the unseen BD modes at time 400. In this case, it means that 0.0257 new BD modes are discovered per hour, or one new BD mode is discovered every 38.9 hours.
Based on Eqn. (Nominal Growth Potential failure intensity), the nominal growth potential failure intensity is:
This is the minimum attainable failure intensity if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
From Eqn. (Nominal Growth Potential MTBF), the nominal growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NGP}}= & \frac{1}{{{\lambda }_{NGP}}} \\ & = & \frac{1}{0.080} \\ & = & 12.37 \end{align} }[/math]
This is the maximum attainable MTBF if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
- 8) From Eqn. (Nominal projected failure intensity), the nominal projected failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{NP}}= & {{\lambda }_{NGP}}+{{d}_{N}}h(400) \\ & = & 0.080+0.6992\cdot 0.0257 \\ & = & 0.0988 \end{align} }[/math]
This is the projected failure intensity assuming all delayed fixes have been implemented for the modes that have been seen.
The nominal projected MTBF at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NP}}= & \frac{1}{{{\lambda }_{NP}}} \\ & = & \frac{1}{0.0988} \\ & = & 10.11 \end{align} }[/math]
This is the projected MTBF assuming all delayed fixes have been implemented for the modes that have been seen.
- 9) Based on Eqn. (Actual GP FI), the actual growth potential failure intensity is:
This is the minimum attainable failure intensity based on the current management strategy.
The actual growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AGP}}= & \frac{1}{{{\lambda }_{AGP}}} \\ & = & \frac{1}{0.1029} \\ & = & 9.71 \end{align} }[/math]
This is the maximum attainable MTBF based on the current management strategy.
- 10) From Eqn. (Actual projected FI), the actual projected failure intensity at time is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{AP}}= & {{\lambda }_{AGP}}+{{d}_{A}}\cdot h\left( 400 \right) \\ & = & 0.1029+0.3075\cdot 0.0257 \\ & = & 0.1108 \end{align} }[/math]
This is the projected failure intensity based on the current management strategy.
The actual projected MTBF at time is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AP}}= & \frac{1}{{{\lambda }_{AP}}} \\ & = & \frac{1}{0.1108} \\ & = & 9.01 \end{align} }[/math]
This is the projected MTBF based on the current management strategy.
Figure QCP MTBFac demonstrates how we can derive the results of this example by using RGA 7's Quick Calculation Pad (QCP). Here we chose to calculate the actual projected MTBF.
Example 2
The Crow Extended - Continuous Evaluation model allows data analysis across multiple phases, up to seven individual phases. Figure Example2table, 6 phases shows a portion of failure time test results obtained across six phases. Analysis points are specified for continuous evaluation every 1000 hours. The cumulative test times at the end of each test phase are 5000, 15000, 25000, 35000, 45000 and 60000 hours.
Figure EFxample2 shows the effectiveness factors for the BD modes that do not have an associated fix implementation event. In other words, these are unfixed BD modes. Note that this specifies the phase after which the BD mode will be fixed, if any.
[math]\displaystyle{ }[/math]
Figure Example2Plot shows the overall test results in terms of demonstrated, projected and growth potential MTBF.
[math]\displaystyle{ }[/math]
Figure Indivdual Mode MTBF shows the Before and After MTBFs for all the individual modes. Note that the After MTBFs are calculated by taking into account the respective effectiveness factors for each of the unfixed BD modes.
[math]\displaystyle{ }[/math]
The analysis points are used to track overall growth inside and across phases, at desired intervals. A multi-phase plot can be created by right-clicking Additional Plots in the Project Explorer and selecting Add MultiPhase Plot. The MultiPhase Plot Wizard guides you through the process concerning the data sheet selection. Since the Crow Extended - Continuous Evaluation was used for the six-phase test, we select the Multi-Phase option.
A Multi-Phase data sheet can be associated with the multi-phase plot. Also, if there is an existing Planning folio, the multi-phase plot can bring the test results together with the Planning. This allows you to track the overall reliability program against the goals and set plans at each stage of the test. Additional information on combining a Planning folio and a MultiPhase plot is presented in Chapter 11.
Figure Multi-phase plot shows the multi-phase plot for the six phases of the reliability growth test program. This plot can be a powerful tool for overall tracking of the reliability growth program. It displays the termination time for each phase of testing along with the demonstrated, projected and growth potential MTBFs at those times. The plot also displays these calculated MTBFs at specified analysis points, which are determined based on the "AP" events in the data sheet.
[math]\displaystyle{ }[/math]
Template loop detected: Template:Discrete data crow rga
Template loop detected: Template:Statistical tests for effectiveness of corrective actions crow rga
As discussed in the previous chapter, the Crow Extended model is designed for a single test phase. However, in most cases testing for a system will be conducted in multiple phases. The Crow Extended - Continuous Evaluation model is designed for analyzing data across multiple test phases, while considering the data for all phases as one data set. In the RGA software, it is applied when using the Multi-Phase data sheet.
The Crow Extended - Continuous Evaluation (3-parameter) model is an extension of the Crow Extended model, and is designed for the practical testing situation where we need the flexibility to apply corrective actions at the time of failure or at a later time during the test, at the end of the current test or during a subsequent test phase. This three-parameter model is free of the constraint that testing must be stopped and all BD modes must be corrected at the end of the test, as in the Crow Extended model. The failure modes can be corrected during the test or when the testing is stopped for the incorporation of the fixes, or even not corrected at all at the end of the test phase. Based on this flexibility, the end time of testing is also not predefined, and it can be continuously updated with new test data, and this is the reason behind the naming, continuous evaluation.
Definitions
Template loop detected: Template:Classifications crow rga Template loop detected: Template:Event codes crow rga
Template loop detected: Template:P ratio crow rga
Template loop detected: Template:Effectiveness factor crow rga
Template loop detected: Template:Growth potential and projections crow rga
Example 1
Table 10.2 shows the Multi-Phase data with failure and fix implementation events. Figure Example 1 data in RGA 7 shows the Table 10.2 data as entered in RGA 7. Note that since this is a time terminated test with a single phase ending at [math]\displaystyle{ T=400 }[/math] , the last event entry is a phase (PH) with time to event = 400.
| Table 10.2 - Multi-Phase data for a time terminated test at [math]\displaystyle{ T=400 }[/math] | ||||||||
| Event | Time to Event | Classification | Mode | Event | Time to Event | Classification | Mode | |
|---|---|---|---|---|---|---|---|---|
| F | 0.7 | BD | 1000 | F | 244.8 | A | 3 | |
| F | 15 | BD | 2000 | F | 249 | BD | 13000 | |
| F | 17.6 | BC | 200 | F | 250.8 | A | 2 | |
| F | 25.3 | BD | 3000 | F | 260.1 | BD | 2000 | |
| F | 47.5 | BD | 4000 | F | 273.1 | A | 5 | |
| I | 50 | BD | 1000 | F | 274.7 | BD | 11000 | |
| F | 54 | BD | 5000 | I | 280 | BD | 9000 | |
| F | 54.5 | BC | 300 | F | 282.8 | BC | 902 | |
| F | 56.4 | BD | 6000 | F | 285 | BD | 14000 | |
| F | 63.6 | A | 1 | F | 315.4 | BD | 4000 | |
| F | 72.2 | BD | 5000 | F | 317.1 | A | 3 | |
| F | 99.2 | BC | 400 | F | 320.6 | A | 1 | |
| F | 99.6 | BD | 7000 | F | 324.5 | BD | 12000 | |
| F | 100.3 | BD | 8000 | F | 324.9 | BD | 10000 | |
| F | 102.5 | A | 2 | F | 342 | BD | 5000 | |
| F | 112 | BD | 9000 | F | 350.2 | BD | 3000 | |
| F | 112.2 | BC | 500 | F | 355.2 | BC | 903 | |
| F | 120.9 | BD | 2000 | F | 364.6 | BD | 10000 | |
| F | 121.9 | BC | 600 | F | 364.9 | A | 1 | |
| F | 125.5 | BD | 10000 | I | 365 | BD | 10000 | |
| F | 133.4 | BD | 11000 | F | 366.3 | BD | 2000 | |
| F | 151 | BC | 700 | F | 379.4 | BD | 15000 | |
| F | 163 | BC | 800 | F | 389 | BD | 16000 | |
| F | 174.5 | BC | 900 | I | 390 | BD | 15000 | |
| F | 177.4 | BD | 10000 | I | 393 | BD | 16000 | |
| F | 191.6 | BC | 901 | F | 394.9 | A | 3 | |
| F | 192.7 | BD | 12000 | F | 395.2 | BD | 17000 | |
| F | 213 | A | 1 | |||||
Figure EF example 1 shows the effectiveness factors for the unfixed BD modes and information concerning whether the fix will be implemented. Since we have only one test phase for this example, a 1 indicates that the fix will be implemented at the end of the first (and only) phase.
Do the following:
- 1) Determine the current demonstrated MTBF and failure intensity at time [math]\displaystyle{ T }[/math] .
- 2) Determine the nominal and actual average effectiveness factor at time [math]\displaystyle{ T }[/math] .
- 3) Determine the ratio.
- 4) Determine the nominal and actual growth potential factor.
- 5) Determine the unfixed BD mode failure intensity at time [math]\displaystyle{ T. }[/math]
- 6) Determine the rate of discovery parameters and the rate of discovery function at time [math]\displaystyle{ T }[/math] .
- 7) Determine the nominal growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 8) Determine the nominal projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 9) Determine the actual growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 10) Determine the actual projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
Solution
- 1) As seen in Chapter 5, for a time terminated test, [math]\displaystyle{ \beta }[/math] is estimated by the following equation:
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
where in this case [math]\displaystyle{ {{T}^{*}}= }[/math] termination time [math]\displaystyle{ =400, }[/math] and [math]\displaystyle{ n }[/math] is the total number of failures. In this example [math]\displaystyle{ n=50 }[/math] . Note that there are five fix implementation events and one event that marks the end of the phase. These should not be counted as failures.
So in this case we find that [math]\displaystyle{ \beta =0.9866. }[/math]
Note that here we calculated the biased estimate of [math]\displaystyle{ \beta }[/math] but we could have used the unbiased estimate as presented in Chapter 5. The choice of calculating the biased or unbiased estimate of [math]\displaystyle{ \beta }[/math] can be set in the User Setup in RGA 7.
Then solve for [math]\displaystyle{ \lambda , }[/math] based on the Crow-AMSAA (NHPP) equation explained in Chapter 5, Section 5.1.1:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{n}{{{T}^{*\beta }}} \\ & = & \frac{50}{{{400}^{0.9866}}} \\ & = & 0.1354 \end{align} }[/math]
The demonstrated MTBF of the system at time [math]\displaystyle{ T=400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{D}}= & \frac{1}{\lambda \beta {{T}^{\beta -1}}} \\ & = & 8.1087 \end{align} }[/math]
The corresponding current demonstrated failure intensity is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{D}}= & \frac{1}{MTB{{F}_{D}}} \\ & = & 0.1233 \end{align} }[/math]
- 2) The average nominal effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average Nominal EF):
- [math]\displaystyle{ \begin{align} & {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ & = & \frac{0.67+0.72+0.77+0.77+0.87+0.92+0.5+0.74+0.7+0.63+0.64+0.46}{12} \\ & = & 0.6992 \end{align} }[/math]
The average actual effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average actual EF):
- [math]\displaystyle{ \begin{align} & {{d}_{A}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M} \\ & = & \frac{0.67+0+0.77+0+0.87+0+0+0.74+0+0+0.64+0}{12} \\ & = & 0.3075 \end{align} }[/math]
- 3) The [math]\displaystyle{ p }[/math] ratio is calculated by using Eqn. (p ratio):
- [math]\displaystyle{ \begin{align} & p= & \frac{\text{Total number of distinct unfixed BD modes at time }400}{\text{Total number of distinct BD modes at time }400\text{ (both fixed and unfixed)}} \\ & = & \frac{12}{12+5} \\ & = & 0.7059 \end{align} }[/math]
- 4) The nominal growth potential factor is given by Eqn. (Nonimal GP Factor) :
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ni}} \right)\frac{{{N}_{i}}}{T} }[/math]
The total number [math]\displaystyle{ M }[/math] of distinct unfixed BD modes at time [math]\displaystyle{ 400 }[/math] is [math]\displaystyle{ M=12. }[/math]
- [math]\displaystyle{ {{d}_{Ni}} }[/math] is the assigned (nominal) EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}}, }[/math] (as given in Figure EF example 1).
- [math]\displaystyle{ {{N}_{i}} }[/math] is the total number of failures over (0, [math]\displaystyle{ 400 }[/math] ) for the distinct unfixed BD mode [math]\displaystyle{ i }[/math] . This is summarized in Table 10.3.
| Table 10.3 - Number of failures for unfixed BD modes | ||
| Classification | Mode | Number of Failures |
|---|---|---|
| BD | 2000 | 4 |
| BD | 3000 | 2 |
| BD | 4000 | 2 |
| BD | 5000 | 3 |
| BD | 6000 | 1 |
| BD | 7000 | 1 |
| BD | 8000 | 1 |
| BD | 11000 | 2 |
| BD | 12000 | 2 |
| BD | 13000 | 1 |
| BD | 14000 | 1 |
| BD | 17000 | 1 |
| Sum = 21 | ||
Based on the above, the nominal growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=0.0153 }[/math]
The actual growth potential factor is given by Eqn. (Actual GP factor):
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ai}} \right)\frac{{{N}_{i}}}{T} }[/math]
where [math]\displaystyle{ {{d}_{Ai}} }[/math] is the actual EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time 400, depending on whether a fix was implemented at time 400 or not. Figure Event report example 1 shows an event report from RGA 7 where it can be seen that the actual EF is zero if a fix was not implemented at 400, or equal to the nominal EF if the fix was implemented at 400.
Based on the above, the actual growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=0.0344 }[/math]
- 5) The total number of unfixed BD modes is 21, based on Table 10.2. From Eqn. (lambdaBDunfixed), the unfixed BD mode failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- 6) The discovery rate parameters at time [math]\displaystyle{ 400 }[/math] are calculated using all the first occurrences of all the BD modes, both fixed and unfixed. [math]\displaystyle{ {{\widehat{\beta }}_{BD}} }[/math] is the unbiased estimated of [math]\displaystyle{ \beta }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes in our example. [math]\displaystyle{ {{\widehat{\lambda }}_{BD}} }[/math] is the unbiased estimate of [math]\displaystyle{ \lambda }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the [math]\displaystyle{ 17 }[/math] distinct BD modes. Figure first occurence BD shows the first time to failure for each of the 17 distinct modes and the results of the analysis using the Crow-AMSAA (NHPP) model in RGA 7 (note that the calculation settings in the User Setup have to be set to calculate unbiased [math]\displaystyle{ \beta }[/math] in this case).
So we have:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6055 }[/math]
- and:
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.4518 }[/math]
The equations used to determine these parameters have been explained in question 1 of this example and are also presented in detail in Chapter 5, Section 5.1.1.
Based on Eqn. (Discovery Function), the discovery rate function at time 400 is:
- [math]\displaystyle{ \begin{align} & \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & 0.4518\cdot 0.6055\cdot {{400}^{0.6055-1}} \\ & = & 0.0257 \end{align} }[/math]
This is the failure intensity of the unseen BD modes at time 400. In this case, it means that 0.0257 new BD modes are discovered per hour, or one new BD mode is discovered every 38.9 hours.
Based on Eqn. (Nominal Growth Potential failure intensity), the nominal growth potential failure intensity is:
This is the minimum attainable failure intensity if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
From Eqn. (Nominal Growth Potential MTBF), the nominal growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NGP}}= & \frac{1}{{{\lambda }_{NGP}}} \\ & = & \frac{1}{0.080} \\ & = & 12.37 \end{align} }[/math]
This is the maximum attainable MTBF if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
- 8) From Eqn. (Nominal projected failure intensity), the nominal projected failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{NP}}= & {{\lambda }_{NGP}}+{{d}_{N}}h(400) \\ & = & 0.080+0.6992\cdot 0.0257 \\ & = & 0.0988 \end{align} }[/math]
This is the projected failure intensity assuming all delayed fixes have been implemented for the modes that have been seen.
The nominal projected MTBF at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NP}}= & \frac{1}{{{\lambda }_{NP}}} \\ & = & \frac{1}{0.0988} \\ & = & 10.11 \end{align} }[/math]
This is the projected MTBF assuming all delayed fixes have been implemented for the modes that have been seen.
- 9) Based on Eqn. (Actual GP FI), the actual growth potential failure intensity is:
This is the minimum attainable failure intensity based on the current management strategy.
The actual growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AGP}}= & \frac{1}{{{\lambda }_{AGP}}} \\ & = & \frac{1}{0.1029} \\ & = & 9.71 \end{align} }[/math]
This is the maximum attainable MTBF based on the current management strategy.
- 10) From Eqn. (Actual projected FI), the actual projected failure intensity at time is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{AP}}= & {{\lambda }_{AGP}}+{{d}_{A}}\cdot h\left( 400 \right) \\ & = & 0.1029+0.3075\cdot 0.0257 \\ & = & 0.1108 \end{align} }[/math]
This is the projected failure intensity based on the current management strategy.
The actual projected MTBF at time is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AP}}= & \frac{1}{{{\lambda }_{AP}}} \\ & = & \frac{1}{0.1108} \\ & = & 9.01 \end{align} }[/math]
This is the projected MTBF based on the current management strategy.
Figure QCP MTBFac demonstrates how we can derive the results of this example by using RGA 7's Quick Calculation Pad (QCP). Here we chose to calculate the actual projected MTBF.
Example 2
The Crow Extended - Continuous Evaluation model allows data analysis across multiple phases, up to seven individual phases. Figure Example2table, 6 phases shows a portion of failure time test results obtained across six phases. Analysis points are specified for continuous evaluation every 1000 hours. The cumulative test times at the end of each test phase are 5000, 15000, 25000, 35000, 45000 and 60000 hours.
Figure EFxample2 shows the effectiveness factors for the BD modes that do not have an associated fix implementation event. In other words, these are unfixed BD modes. Note that this specifies the phase after which the BD mode will be fixed, if any.
[math]\displaystyle{ }[/math]
Figure Example2Plot shows the overall test results in terms of demonstrated, projected and growth potential MTBF.
[math]\displaystyle{ }[/math]
Figure Indivdual Mode MTBF shows the Before and After MTBFs for all the individual modes. Note that the After MTBFs are calculated by taking into account the respective effectiveness factors for each of the unfixed BD modes.
[math]\displaystyle{ }[/math]
The analysis points are used to track overall growth inside and across phases, at desired intervals. A multi-phase plot can be created by right-clicking Additional Plots in the Project Explorer and selecting Add MultiPhase Plot. The MultiPhase Plot Wizard guides you through the process concerning the data sheet selection. Since the Crow Extended - Continuous Evaluation was used for the six-phase test, we select the Multi-Phase option.
A Multi-Phase data sheet can be associated with the multi-phase plot. Also, if there is an existing Planning folio, the multi-phase plot can bring the test results together with the Planning. This allows you to track the overall reliability program against the goals and set plans at each stage of the test. Additional information on combining a Planning folio and a MultiPhase plot is presented in Chapter 11.
Figure Multi-phase plot shows the multi-phase plot for the six phases of the reliability growth test program. This plot can be a powerful tool for overall tracking of the reliability growth program. It displays the termination time for each phase of testing along with the demonstrated, projected and growth potential MTBFs at those times. The plot also displays these calculated MTBFs at specified analysis points, which are determined based on the "AP" events in the data sheet.
[math]\displaystyle{ }[/math]
Template loop detected: Template:Discrete data crow rga
Template loop detected: Template:Statistical tests for effectiveness of corrective actions crow rga
As discussed in the previous chapter, the Crow Extended model is designed for a single test phase. However, in most cases testing for a system will be conducted in multiple phases. The Crow Extended - Continuous Evaluation model is designed for analyzing data across multiple test phases, while considering the data for all phases as one data set. In the RGA software, it is applied when using the Multi-Phase data sheet.
The Crow Extended - Continuous Evaluation (3-parameter) model is an extension of the Crow Extended model, and is designed for the practical testing situation where we need the flexibility to apply corrective actions at the time of failure or at a later time during the test, at the end of the current test or during a subsequent test phase. This three-parameter model is free of the constraint that testing must be stopped and all BD modes must be corrected at the end of the test, as in the Crow Extended model. The failure modes can be corrected during the test or when the testing is stopped for the incorporation of the fixes, or even not corrected at all at the end of the test phase. Based on this flexibility, the end time of testing is also not predefined, and it can be continuously updated with new test data, and this is the reason behind the naming, continuous evaluation.
Definitions
Template loop detected: Template:Classifications crow rga Template loop detected: Template:Event codes crow rga
Template loop detected: Template:P ratio crow rga
Template loop detected: Template:Effectiveness factor crow rga
Template loop detected: Template:Growth potential and projections crow rga
Example 1
Table 10.2 shows the Multi-Phase data with failure and fix implementation events. Figure Example 1 data in RGA 7 shows the Table 10.2 data as entered in RGA 7. Note that since this is a time terminated test with a single phase ending at [math]\displaystyle{ T=400 }[/math] , the last event entry is a phase (PH) with time to event = 400.
| Table 10.2 - Multi-Phase data for a time terminated test at [math]\displaystyle{ T=400 }[/math] | ||||||||
| Event | Time to Event | Classification | Mode | Event | Time to Event | Classification | Mode | |
|---|---|---|---|---|---|---|---|---|
| F | 0.7 | BD | 1000 | F | 244.8 | A | 3 | |
| F | 15 | BD | 2000 | F | 249 | BD | 13000 | |
| F | 17.6 | BC | 200 | F | 250.8 | A | 2 | |
| F | 25.3 | BD | 3000 | F | 260.1 | BD | 2000 | |
| F | 47.5 | BD | 4000 | F | 273.1 | A | 5 | |
| I | 50 | BD | 1000 | F | 274.7 | BD | 11000 | |
| F | 54 | BD | 5000 | I | 280 | BD | 9000 | |
| F | 54.5 | BC | 300 | F | 282.8 | BC | 902 | |
| F | 56.4 | BD | 6000 | F | 285 | BD | 14000 | |
| F | 63.6 | A | 1 | F | 315.4 | BD | 4000 | |
| F | 72.2 | BD | 5000 | F | 317.1 | A | 3 | |
| F | 99.2 | BC | 400 | F | 320.6 | A | 1 | |
| F | 99.6 | BD | 7000 | F | 324.5 | BD | 12000 | |
| F | 100.3 | BD | 8000 | F | 324.9 | BD | 10000 | |
| F | 102.5 | A | 2 | F | 342 | BD | 5000 | |
| F | 112 | BD | 9000 | F | 350.2 | BD | 3000 | |
| F | 112.2 | BC | 500 | F | 355.2 | BC | 903 | |
| F | 120.9 | BD | 2000 | F | 364.6 | BD | 10000 | |
| F | 121.9 | BC | 600 | F | 364.9 | A | 1 | |
| F | 125.5 | BD | 10000 | I | 365 | BD | 10000 | |
| F | 133.4 | BD | 11000 | F | 366.3 | BD | 2000 | |
| F | 151 | BC | 700 | F | 379.4 | BD | 15000 | |
| F | 163 | BC | 800 | F | 389 | BD | 16000 | |
| F | 174.5 | BC | 900 | I | 390 | BD | 15000 | |
| F | 177.4 | BD | 10000 | I | 393 | BD | 16000 | |
| F | 191.6 | BC | 901 | F | 394.9 | A | 3 | |
| F | 192.7 | BD | 12000 | F | 395.2 | BD | 17000 | |
| F | 213 | A | 1 | |||||
Figure EF example 1 shows the effectiveness factors for the unfixed BD modes and information concerning whether the fix will be implemented. Since we have only one test phase for this example, a 1 indicates that the fix will be implemented at the end of the first (and only) phase.
Do the following:
- 1) Determine the current demonstrated MTBF and failure intensity at time [math]\displaystyle{ T }[/math] .
- 2) Determine the nominal and actual average effectiveness factor at time [math]\displaystyle{ T }[/math] .
- 3) Determine the ratio.
- 4) Determine the nominal and actual growth potential factor.
- 5) Determine the unfixed BD mode failure intensity at time [math]\displaystyle{ T. }[/math]
- 6) Determine the rate of discovery parameters and the rate of discovery function at time [math]\displaystyle{ T }[/math] .
- 7) Determine the nominal growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 8) Determine the nominal projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 9) Determine the actual growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 10) Determine the actual projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
Solution
- 1) As seen in Chapter 5, for a time terminated test, [math]\displaystyle{ \beta }[/math] is estimated by the following equation:
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
where in this case [math]\displaystyle{ {{T}^{*}}= }[/math] termination time [math]\displaystyle{ =400, }[/math] and [math]\displaystyle{ n }[/math] is the total number of failures. In this example [math]\displaystyle{ n=50 }[/math] . Note that there are five fix implementation events and one event that marks the end of the phase. These should not be counted as failures.
So in this case we find that [math]\displaystyle{ \beta =0.9866. }[/math]
Note that here we calculated the biased estimate of [math]\displaystyle{ \beta }[/math] but we could have used the unbiased estimate as presented in Chapter 5. The choice of calculating the biased or unbiased estimate of [math]\displaystyle{ \beta }[/math] can be set in the User Setup in RGA 7.
Then solve for [math]\displaystyle{ \lambda , }[/math] based on the Crow-AMSAA (NHPP) equation explained in Chapter 5, Section 5.1.1:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{n}{{{T}^{*\beta }}} \\ & = & \frac{50}{{{400}^{0.9866}}} \\ & = & 0.1354 \end{align} }[/math]
The demonstrated MTBF of the system at time [math]\displaystyle{ T=400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{D}}= & \frac{1}{\lambda \beta {{T}^{\beta -1}}} \\ & = & 8.1087 \end{align} }[/math]
The corresponding current demonstrated failure intensity is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{D}}= & \frac{1}{MTB{{F}_{D}}} \\ & = & 0.1233 \end{align} }[/math]
- 2) The average nominal effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average Nominal EF):
- [math]\displaystyle{ \begin{align} & {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ & = & \frac{0.67+0.72+0.77+0.77+0.87+0.92+0.5+0.74+0.7+0.63+0.64+0.46}{12} \\ & = & 0.6992 \end{align} }[/math]
The average actual effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average actual EF):
- [math]\displaystyle{ \begin{align} & {{d}_{A}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M} \\ & = & \frac{0.67+0+0.77+0+0.87+0+0+0.74+0+0+0.64+0}{12} \\ & = & 0.3075 \end{align} }[/math]
- 3) The [math]\displaystyle{ p }[/math] ratio is calculated by using Eqn. (p ratio):
- [math]\displaystyle{ \begin{align} & p= & \frac{\text{Total number of distinct unfixed BD modes at time }400}{\text{Total number of distinct BD modes at time }400\text{ (both fixed and unfixed)}} \\ & = & \frac{12}{12+5} \\ & = & 0.7059 \end{align} }[/math]
- 4) The nominal growth potential factor is given by Eqn. (Nonimal GP Factor) :
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ni}} \right)\frac{{{N}_{i}}}{T} }[/math]
The total number [math]\displaystyle{ M }[/math] of distinct unfixed BD modes at time [math]\displaystyle{ 400 }[/math] is [math]\displaystyle{ M=12. }[/math]
- [math]\displaystyle{ {{d}_{Ni}} }[/math] is the assigned (nominal) EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}}, }[/math] (as given in Figure EF example 1).
- [math]\displaystyle{ {{N}_{i}} }[/math] is the total number of failures over (0, [math]\displaystyle{ 400 }[/math] ) for the distinct unfixed BD mode [math]\displaystyle{ i }[/math] . This is summarized in Table 10.3.
| Table 10.3 - Number of failures for unfixed BD modes | ||
| Classification | Mode | Number of Failures |
|---|---|---|
| BD | 2000 | 4 |
| BD | 3000 | 2 |
| BD | 4000 | 2 |
| BD | 5000 | 3 |
| BD | 6000 | 1 |
| BD | 7000 | 1 |
| BD | 8000 | 1 |
| BD | 11000 | 2 |
| BD | 12000 | 2 |
| BD | 13000 | 1 |
| BD | 14000 | 1 |
| BD | 17000 | 1 |
| Sum = 21 | ||
Based on the above, the nominal growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=0.0153 }[/math]
The actual growth potential factor is given by Eqn. (Actual GP factor):
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ai}} \right)\frac{{{N}_{i}}}{T} }[/math]
where [math]\displaystyle{ {{d}_{Ai}} }[/math] is the actual EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time 400, depending on whether a fix was implemented at time 400 or not. Figure Event report example 1 shows an event report from RGA 7 where it can be seen that the actual EF is zero if a fix was not implemented at 400, or equal to the nominal EF if the fix was implemented at 400.
Based on the above, the actual growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=0.0344 }[/math]
- 5) The total number of unfixed BD modes is 21, based on Table 10.2. From Eqn. (lambdaBDunfixed), the unfixed BD mode failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- 6) The discovery rate parameters at time [math]\displaystyle{ 400 }[/math] are calculated using all the first occurrences of all the BD modes, both fixed and unfixed. [math]\displaystyle{ {{\widehat{\beta }}_{BD}} }[/math] is the unbiased estimated of [math]\displaystyle{ \beta }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes in our example. [math]\displaystyle{ {{\widehat{\lambda }}_{BD}} }[/math] is the unbiased estimate of [math]\displaystyle{ \lambda }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the [math]\displaystyle{ 17 }[/math] distinct BD modes. Figure first occurence BD shows the first time to failure for each of the 17 distinct modes and the results of the analysis using the Crow-AMSAA (NHPP) model in RGA 7 (note that the calculation settings in the User Setup have to be set to calculate unbiased [math]\displaystyle{ \beta }[/math] in this case).
So we have:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6055 }[/math]
- and:
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.4518 }[/math]
The equations used to determine these parameters have been explained in question 1 of this example and are also presented in detail in Chapter 5, Section 5.1.1.
Based on Eqn. (Discovery Function), the discovery rate function at time 400 is:
- [math]\displaystyle{ \begin{align} & \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & 0.4518\cdot 0.6055\cdot {{400}^{0.6055-1}} \\ & = & 0.0257 \end{align} }[/math]
This is the failure intensity of the unseen BD modes at time 400. In this case, it means that 0.0257 new BD modes are discovered per hour, or one new BD mode is discovered every 38.9 hours.
Based on Eqn. (Nominal Growth Potential failure intensity), the nominal growth potential failure intensity is:
This is the minimum attainable failure intensity if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
From Eqn. (Nominal Growth Potential MTBF), the nominal growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NGP}}= & \frac{1}{{{\lambda }_{NGP}}} \\ & = & \frac{1}{0.080} \\ & = & 12.37 \end{align} }[/math]
This is the maximum attainable MTBF if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
- 8) From Eqn. (Nominal projected failure intensity), the nominal projected failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{NP}}= & {{\lambda }_{NGP}}+{{d}_{N}}h(400) \\ & = & 0.080+0.6992\cdot 0.0257 \\ & = & 0.0988 \end{align} }[/math]
This is the projected failure intensity assuming all delayed fixes have been implemented for the modes that have been seen.
The nominal projected MTBF at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NP}}= & \frac{1}{{{\lambda }_{NP}}} \\ & = & \frac{1}{0.0988} \\ & = & 10.11 \end{align} }[/math]
This is the projected MTBF assuming all delayed fixes have been implemented for the modes that have been seen.
- 9) Based on Eqn. (Actual GP FI), the actual growth potential failure intensity is:
This is the minimum attainable failure intensity based on the current management strategy.
The actual growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AGP}}= & \frac{1}{{{\lambda }_{AGP}}} \\ & = & \frac{1}{0.1029} \\ & = & 9.71 \end{align} }[/math]
This is the maximum attainable MTBF based on the current management strategy.
- 10) From Eqn. (Actual projected FI), the actual projected failure intensity at time is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{AP}}= & {{\lambda }_{AGP}}+{{d}_{A}}\cdot h\left( 400 \right) \\ & = & 0.1029+0.3075\cdot 0.0257 \\ & = & 0.1108 \end{align} }[/math]
This is the projected failure intensity based on the current management strategy.
The actual projected MTBF at time is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AP}}= & \frac{1}{{{\lambda }_{AP}}} \\ & = & \frac{1}{0.1108} \\ & = & 9.01 \end{align} }[/math]
This is the projected MTBF based on the current management strategy.
Figure QCP MTBFac demonstrates how we can derive the results of this example by using RGA 7's Quick Calculation Pad (QCP). Here we chose to calculate the actual projected MTBF.
Example 2
The Crow Extended - Continuous Evaluation model allows data analysis across multiple phases, up to seven individual phases. Figure Example2table, 6 phases shows a portion of failure time test results obtained across six phases. Analysis points are specified for continuous evaluation every 1000 hours. The cumulative test times at the end of each test phase are 5000, 15000, 25000, 35000, 45000 and 60000 hours.
Figure EFxample2 shows the effectiveness factors for the BD modes that do not have an associated fix implementation event. In other words, these are unfixed BD modes. Note that this specifies the phase after which the BD mode will be fixed, if any.
[math]\displaystyle{ }[/math]
Figure Example2Plot shows the overall test results in terms of demonstrated, projected and growth potential MTBF.
[math]\displaystyle{ }[/math]
Figure Indivdual Mode MTBF shows the Before and After MTBFs for all the individual modes. Note that the After MTBFs are calculated by taking into account the respective effectiveness factors for each of the unfixed BD modes.
[math]\displaystyle{ }[/math]
The analysis points are used to track overall growth inside and across phases, at desired intervals. A multi-phase plot can be created by right-clicking Additional Plots in the Project Explorer and selecting Add MultiPhase Plot. The MultiPhase Plot Wizard guides you through the process concerning the data sheet selection. Since the Crow Extended - Continuous Evaluation was used for the six-phase test, we select the Multi-Phase option.
A Multi-Phase data sheet can be associated with the multi-phase plot. Also, if there is an existing Planning folio, the multi-phase plot can bring the test results together with the Planning. This allows you to track the overall reliability program against the goals and set plans at each stage of the test. Additional information on combining a Planning folio and a MultiPhase plot is presented in Chapter 11.
Figure Multi-phase plot shows the multi-phase plot for the six phases of the reliability growth test program. This plot can be a powerful tool for overall tracking of the reliability growth program. It displays the termination time for each phase of testing along with the demonstrated, projected and growth potential MTBFs at those times. The plot also displays these calculated MTBFs at specified analysis points, which are determined based on the "AP" events in the data sheet.
[math]\displaystyle{ }[/math]
Template loop detected: Template:Discrete data crow rga
Template loop detected: Template:Statistical tests for effectiveness of corrective actions crow rga
Example 1
Table 10.2 shows the Multi-Phase data with failure and fix implementation events. Figure Example 1 data in RGA 7 shows the Table 10.2 data as entered in RGA 7. Note that since this is a time terminated test with a single phase ending at [math]\displaystyle{ T=400 }[/math] , the last event entry is a phase (PH) with time to event = 400.
| Table 10.2 - Multi-Phase data for a time terminated test at [math]\displaystyle{ T=400 }[/math] | ||||||||
| Event | Time to Event | Classification | Mode | Event | Time to Event | Classification | Mode | |
|---|---|---|---|---|---|---|---|---|
| F | 0.7 | BD | 1000 | F | 244.8 | A | 3 | |
| F | 15 | BD | 2000 | F | 249 | BD | 13000 | |
| F | 17.6 | BC | 200 | F | 250.8 | A | 2 | |
| F | 25.3 | BD | 3000 | F | 260.1 | BD | 2000 | |
| F | 47.5 | BD | 4000 | F | 273.1 | A | 5 | |
| I | 50 | BD | 1000 | F | 274.7 | BD | 11000 | |
| F | 54 | BD | 5000 | I | 280 | BD | 9000 | |
| F | 54.5 | BC | 300 | F | 282.8 | BC | 902 | |
| F | 56.4 | BD | 6000 | F | 285 | BD | 14000 | |
| F | 63.6 | A | 1 | F | 315.4 | BD | 4000 | |
| F | 72.2 | BD | 5000 | F | 317.1 | A | 3 | |
| F | 99.2 | BC | 400 | F | 320.6 | A | 1 | |
| F | 99.6 | BD | 7000 | F | 324.5 | BD | 12000 | |
| F | 100.3 | BD | 8000 | F | 324.9 | BD | 10000 | |
| F | 102.5 | A | 2 | F | 342 | BD | 5000 | |
| F | 112 | BD | 9000 | F | 350.2 | BD | 3000 | |
| F | 112.2 | BC | 500 | F | 355.2 | BC | 903 | |
| F | 120.9 | BD | 2000 | F | 364.6 | BD | 10000 | |
| F | 121.9 | BC | 600 | F | 364.9 | A | 1 | |
| F | 125.5 | BD | 10000 | I | 365 | BD | 10000 | |
| F | 133.4 | BD | 11000 | F | 366.3 | BD | 2000 | |
| F | 151 | BC | 700 | F | 379.4 | BD | 15000 | |
| F | 163 | BC | 800 | F | 389 | BD | 16000 | |
| F | 174.5 | BC | 900 | I | 390 | BD | 15000 | |
| F | 177.4 | BD | 10000 | I | 393 | BD | 16000 | |
| F | 191.6 | BC | 901 | F | 394.9 | A | 3 | |
| F | 192.7 | BD | 12000 | F | 395.2 | BD | 17000 | |
| F | 213 | A | 1 | |||||
Figure EF example 1 shows the effectiveness factors for the unfixed BD modes and information concerning whether the fix will be implemented. Since we have only one test phase for this example, a 1 indicates that the fix will be implemented at the end of the first (and only) phase.
Do the following:
- 1) Determine the current demonstrated MTBF and failure intensity at time [math]\displaystyle{ T }[/math] .
- 2) Determine the nominal and actual average effectiveness factor at time [math]\displaystyle{ T }[/math] .
- 3) Determine the ratio.
- 4) Determine the nominal and actual growth potential factor.
- 5) Determine the unfixed BD mode failure intensity at time [math]\displaystyle{ T. }[/math]
- 6) Determine the rate of discovery parameters and the rate of discovery function at time [math]\displaystyle{ T }[/math] .
- 7) Determine the nominal growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 8) Determine the nominal projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 9) Determine the actual growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 10) Determine the actual projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
Solution
- 1) As seen in Chapter 5, for a time terminated test, [math]\displaystyle{ \beta }[/math] is estimated by the following equation:
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
where in this case [math]\displaystyle{ {{T}^{*}}= }[/math] termination time [math]\displaystyle{ =400, }[/math] and [math]\displaystyle{ n }[/math] is the total number of failures. In this example [math]\displaystyle{ n=50 }[/math] . Note that there are five fix implementation events and one event that marks the end of the phase. These should not be counted as failures.
So in this case we find that [math]\displaystyle{ \beta =0.9866. }[/math]
Note that here we calculated the biased estimate of [math]\displaystyle{ \beta }[/math] but we could have used the unbiased estimate as presented in Chapter 5. The choice of calculating the biased or unbiased estimate of [math]\displaystyle{ \beta }[/math] can be set in the User Setup in RGA 7.
Then solve for [math]\displaystyle{ \lambda , }[/math] based on the Crow-AMSAA (NHPP) equation explained in Chapter 5, Section 5.1.1:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{n}{{{T}^{*\beta }}} \\ & = & \frac{50}{{{400}^{0.9866}}} \\ & = & 0.1354 \end{align} }[/math]
The demonstrated MTBF of the system at time [math]\displaystyle{ T=400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{D}}= & \frac{1}{\lambda \beta {{T}^{\beta -1}}} \\ & = & 8.1087 \end{align} }[/math]
The corresponding current demonstrated failure intensity is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{D}}= & \frac{1}{MTB{{F}_{D}}} \\ & = & 0.1233 \end{align} }[/math]
- 2) The average nominal effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average Nominal EF):
- [math]\displaystyle{ \begin{align} & {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ & = & \frac{0.67+0.72+0.77+0.77+0.87+0.92+0.5+0.74+0.7+0.63+0.64+0.46}{12} \\ & = & 0.6992 \end{align} }[/math]
The average actual effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average actual EF):
- [math]\displaystyle{ \begin{align} & {{d}_{A}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M} \\ & = & \frac{0.67+0+0.77+0+0.87+0+0+0.74+0+0+0.64+0}{12} \\ & = & 0.3075 \end{align} }[/math]
- 3) The [math]\displaystyle{ p }[/math] ratio is calculated by using Eqn. (p ratio):
- [math]\displaystyle{ \begin{align} & p= & \frac{\text{Total number of distinct unfixed BD modes at time }400}{\text{Total number of distinct BD modes at time }400\text{ (both fixed and unfixed)}} \\ & = & \frac{12}{12+5} \\ & = & 0.7059 \end{align} }[/math]
- 4) The nominal growth potential factor is given by Eqn. (Nonimal GP Factor) :
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ni}} \right)\frac{{{N}_{i}}}{T} }[/math]
The total number [math]\displaystyle{ M }[/math] of distinct unfixed BD modes at time [math]\displaystyle{ 400 }[/math] is [math]\displaystyle{ M=12. }[/math]
- [math]\displaystyle{ {{d}_{Ni}} }[/math] is the assigned (nominal) EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}}, }[/math] (as given in Figure EF example 1).
- [math]\displaystyle{ {{N}_{i}} }[/math] is the total number of failures over (0, [math]\displaystyle{ 400 }[/math] ) for the distinct unfixed BD mode [math]\displaystyle{ i }[/math] . This is summarized in Table 10.3.
| Table 10.3 - Number of failures for unfixed BD modes | ||
| Classification | Mode | Number of Failures |
|---|---|---|
| BD | 2000 | 4 |
| BD | 3000 | 2 |
| BD | 4000 | 2 |
| BD | 5000 | 3 |
| BD | 6000 | 1 |
| BD | 7000 | 1 |
| BD | 8000 | 1 |
| BD | 11000 | 2 |
| BD | 12000 | 2 |
| BD | 13000 | 1 |
| BD | 14000 | 1 |
| BD | 17000 | 1 |
| Sum = 21 | ||
Based on the above, the nominal growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=0.0153 }[/math]
The actual growth potential factor is given by Eqn. (Actual GP factor):
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ai}} \right)\frac{{{N}_{i}}}{T} }[/math]
where [math]\displaystyle{ {{d}_{Ai}} }[/math] is the actual EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time 400, depending on whether a fix was implemented at time 400 or not. Figure Event report example 1 shows an event report from RGA 7 where it can be seen that the actual EF is zero if a fix was not implemented at 400, or equal to the nominal EF if the fix was implemented at 400.
Based on the above, the actual growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=0.0344 }[/math]
- 5) The total number of unfixed BD modes is 21, based on Table 10.2. From Eqn. (lambdaBDunfixed), the unfixed BD mode failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- 6) The discovery rate parameters at time [math]\displaystyle{ 400 }[/math] are calculated using all the first occurrences of all the BD modes, both fixed and unfixed. [math]\displaystyle{ {{\widehat{\beta }}_{BD}} }[/math] is the unbiased estimated of [math]\displaystyle{ \beta }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes in our example. [math]\displaystyle{ {{\widehat{\lambda }}_{BD}} }[/math] is the unbiased estimate of [math]\displaystyle{ \lambda }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the [math]\displaystyle{ 17 }[/math] distinct BD modes. Figure first occurence BD shows the first time to failure for each of the 17 distinct modes and the results of the analysis using the Crow-AMSAA (NHPP) model in RGA 7 (note that the calculation settings in the User Setup have to be set to calculate unbiased [math]\displaystyle{ \beta }[/math] in this case).
So we have:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6055 }[/math]
- and:
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.4518 }[/math]
The equations used to determine these parameters have been explained in question 1 of this example and are also presented in detail in Chapter 5, Section 5.1.1.
Based on Eqn. (Discovery Function), the discovery rate function at time 400 is:
- [math]\displaystyle{ \begin{align} & \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & 0.4518\cdot 0.6055\cdot {{400}^{0.6055-1}} \\ & = & 0.0257 \end{align} }[/math]
This is the failure intensity of the unseen BD modes at time 400. In this case, it means that 0.0257 new BD modes are discovered per hour, or one new BD mode is discovered every 38.9 hours.
Based on Eqn. (Nominal Growth Potential failure intensity), the nominal growth potential failure intensity is:
This is the minimum attainable failure intensity if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
From Eqn. (Nominal Growth Potential MTBF), the nominal growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NGP}}= & \frac{1}{{{\lambda }_{NGP}}} \\ & = & \frac{1}{0.080} \\ & = & 12.37 \end{align} }[/math]
This is the maximum attainable MTBF if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
- 8) From Eqn. (Nominal projected failure intensity), the nominal projected failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{NP}}= & {{\lambda }_{NGP}}+{{d}_{N}}h(400) \\ & = & 0.080+0.6992\cdot 0.0257 \\ & = & 0.0988 \end{align} }[/math]
This is the projected failure intensity assuming all delayed fixes have been implemented for the modes that have been seen.
The nominal projected MTBF at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NP}}= & \frac{1}{{{\lambda }_{NP}}} \\ & = & \frac{1}{0.0988} \\ & = & 10.11 \end{align} }[/math]
This is the projected MTBF assuming all delayed fixes have been implemented for the modes that have been seen.
- 9) Based on Eqn. (Actual GP FI), the actual growth potential failure intensity is:
This is the minimum attainable failure intensity based on the current management strategy.
The actual growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AGP}}= & \frac{1}{{{\lambda }_{AGP}}} \\ & = & \frac{1}{0.1029} \\ & = & 9.71 \end{align} }[/math]
This is the maximum attainable MTBF based on the current management strategy.
- 10) From Eqn. (Actual projected FI), the actual projected failure intensity at time is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{AP}}= & {{\lambda }_{AGP}}+{{d}_{A}}\cdot h\left( 400 \right) \\ & = & 0.1029+0.3075\cdot 0.0257 \\ & = & 0.1108 \end{align} }[/math]
This is the projected failure intensity based on the current management strategy.
The actual projected MTBF at time is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AP}}= & \frac{1}{{{\lambda }_{AP}}} \\ & = & \frac{1}{0.1108} \\ & = & 9.01 \end{align} }[/math]
This is the projected MTBF based on the current management strategy.
Figure QCP MTBFac demonstrates how we can derive the results of this example by using RGA 7's Quick Calculation Pad (QCP). Here we chose to calculate the actual projected MTBF.
Example 2
The Crow Extended - Continuous Evaluation model allows data analysis across multiple phases, up to seven individual phases. Figure Example2table, 6 phases shows a portion of failure time test results obtained across six phases. Analysis points are specified for continuous evaluation every 1000 hours. The cumulative test times at the end of each test phase are 5000, 15000, 25000, 35000, 45000 and 60000 hours.
Figure EFxample2 shows the effectiveness factors for the BD modes that do not have an associated fix implementation event. In other words, these are unfixed BD modes. Note that this specifies the phase after which the BD mode will be fixed, if any.
[math]\displaystyle{ }[/math]
Figure Example2Plot shows the overall test results in terms of demonstrated, projected and growth potential MTBF.
[math]\displaystyle{ }[/math]
Figure Indivdual Mode MTBF shows the Before and After MTBFs for all the individual modes. Note that the After MTBFs are calculated by taking into account the respective effectiveness factors for each of the unfixed BD modes.
[math]\displaystyle{ }[/math]
The analysis points are used to track overall growth inside and across phases, at desired intervals. A multi-phase plot can be created by right-clicking Additional Plots in the Project Explorer and selecting Add MultiPhase Plot. The MultiPhase Plot Wizard guides you through the process concerning the data sheet selection. Since the Crow Extended - Continuous Evaluation was used for the six-phase test, we select the Multi-Phase option.
A Multi-Phase data sheet can be associated with the multi-phase plot. Also, if there is an existing Planning folio, the multi-phase plot can bring the test results together with the Planning. This allows you to track the overall reliability program against the goals and set plans at each stage of the test. Additional information on combining a Planning folio and a MultiPhase plot is presented in Chapter 11.
Figure Multi-phase plot shows the multi-phase plot for the six phases of the reliability growth test program. This plot can be a powerful tool for overall tracking of the reliability growth program. It displays the termination time for each phase of testing along with the demonstrated, projected and growth potential MTBFs at those times. The plot also displays these calculated MTBFs at specified analysis points, which are determined based on the "AP" events in the data sheet.
[math]\displaystyle{ }[/math]
As discussed in the previous chapter, the Crow Extended model is designed for a single test phase. However, in most cases testing for a system will be conducted in multiple phases. The Crow Extended - Continuous Evaluation model is designed for analyzing data across multiple test phases, while considering the data for all phases as one data set. In the RGA software, it is applied when using the Multi-Phase data sheet.
The Crow Extended - Continuous Evaluation (3-parameter) model is an extension of the Crow Extended model, and is designed for the practical testing situation where we need the flexibility to apply corrective actions at the time of failure or at a later time during the test, at the end of the current test or during a subsequent test phase. This three-parameter model is free of the constraint that testing must be stopped and all BD modes must be corrected at the end of the test, as in the Crow Extended model. The failure modes can be corrected during the test or when the testing is stopped for the incorporation of the fixes, or even not corrected at all at the end of the test phase. Based on this flexibility, the end time of testing is also not predefined, and it can be continuously updated with new test data, and this is the reason behind the naming, continuous evaluation.
Definitions
Template loop detected: Template:Classifications crow rga Template loop detected: Template:Event codes crow rga
Template loop detected: Template:P ratio crow rga
Template loop detected: Template:Effectiveness factor crow rga
Template loop detected: Template:Growth potential and projections crow rga
Example 1
Table 10.2 shows the Multi-Phase data with failure and fix implementation events. Figure Example 1 data in RGA 7 shows the Table 10.2 data as entered in RGA 7. Note that since this is a time terminated test with a single phase ending at [math]\displaystyle{ T=400 }[/math] , the last event entry is a phase (PH) with time to event = 400.
| Table 10.2 - Multi-Phase data for a time terminated test at [math]\displaystyle{ T=400 }[/math] | ||||||||
| Event | Time to Event | Classification | Mode | Event | Time to Event | Classification | Mode | |
|---|---|---|---|---|---|---|---|---|
| F | 0.7 | BD | 1000 | F | 244.8 | A | 3 | |
| F | 15 | BD | 2000 | F | 249 | BD | 13000 | |
| F | 17.6 | BC | 200 | F | 250.8 | A | 2 | |
| F | 25.3 | BD | 3000 | F | 260.1 | BD | 2000 | |
| F | 47.5 | BD | 4000 | F | 273.1 | A | 5 | |
| I | 50 | BD | 1000 | F | 274.7 | BD | 11000 | |
| F | 54 | BD | 5000 | I | 280 | BD | 9000 | |
| F | 54.5 | BC | 300 | F | 282.8 | BC | 902 | |
| F | 56.4 | BD | 6000 | F | 285 | BD | 14000 | |
| F | 63.6 | A | 1 | F | 315.4 | BD | 4000 | |
| F | 72.2 | BD | 5000 | F | 317.1 | A | 3 | |
| F | 99.2 | BC | 400 | F | 320.6 | A | 1 | |
| F | 99.6 | BD | 7000 | F | 324.5 | BD | 12000 | |
| F | 100.3 | BD | 8000 | F | 324.9 | BD | 10000 | |
| F | 102.5 | A | 2 | F | 342 | BD | 5000 | |
| F | 112 | BD | 9000 | F | 350.2 | BD | 3000 | |
| F | 112.2 | BC | 500 | F | 355.2 | BC | 903 | |
| F | 120.9 | BD | 2000 | F | 364.6 | BD | 10000 | |
| F | 121.9 | BC | 600 | F | 364.9 | A | 1 | |
| F | 125.5 | BD | 10000 | I | 365 | BD | 10000 | |
| F | 133.4 | BD | 11000 | F | 366.3 | BD | 2000 | |
| F | 151 | BC | 700 | F | 379.4 | BD | 15000 | |
| F | 163 | BC | 800 | F | 389 | BD | 16000 | |
| F | 174.5 | BC | 900 | I | 390 | BD | 15000 | |
| F | 177.4 | BD | 10000 | I | 393 | BD | 16000 | |
| F | 191.6 | BC | 901 | F | 394.9 | A | 3 | |
| F | 192.7 | BD | 12000 | F | 395.2 | BD | 17000 | |
| F | 213 | A | 1 | |||||
Figure EF example 1 shows the effectiveness factors for the unfixed BD modes and information concerning whether the fix will be implemented. Since we have only one test phase for this example, a 1 indicates that the fix will be implemented at the end of the first (and only) phase.
Do the following:
- 1) Determine the current demonstrated MTBF and failure intensity at time [math]\displaystyle{ T }[/math] .
- 2) Determine the nominal and actual average effectiveness factor at time [math]\displaystyle{ T }[/math] .
- 3) Determine the ratio.
- 4) Determine the nominal and actual growth potential factor.
- 5) Determine the unfixed BD mode failure intensity at time [math]\displaystyle{ T. }[/math]
- 6) Determine the rate of discovery parameters and the rate of discovery function at time [math]\displaystyle{ T }[/math] .
- 7) Determine the nominal growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 8) Determine the nominal projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 9) Determine the actual growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 10) Determine the actual projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
Solution
- 1) As seen in Chapter 5, for a time terminated test, [math]\displaystyle{ \beta }[/math] is estimated by the following equation:
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
where in this case [math]\displaystyle{ {{T}^{*}}= }[/math] termination time [math]\displaystyle{ =400, }[/math] and [math]\displaystyle{ n }[/math] is the total number of failures. In this example [math]\displaystyle{ n=50 }[/math] . Note that there are five fix implementation events and one event that marks the end of the phase. These should not be counted as failures.
So in this case we find that [math]\displaystyle{ \beta =0.9866. }[/math]
Note that here we calculated the biased estimate of [math]\displaystyle{ \beta }[/math] but we could have used the unbiased estimate as presented in Chapter 5. The choice of calculating the biased or unbiased estimate of [math]\displaystyle{ \beta }[/math] can be set in the User Setup in RGA 7.
Then solve for [math]\displaystyle{ \lambda , }[/math] based on the Crow-AMSAA (NHPP) equation explained in Chapter 5, Section 5.1.1:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{n}{{{T}^{*\beta }}} \\ & = & \frac{50}{{{400}^{0.9866}}} \\ & = & 0.1354 \end{align} }[/math]
The demonstrated MTBF of the system at time [math]\displaystyle{ T=400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{D}}= & \frac{1}{\lambda \beta {{T}^{\beta -1}}} \\ & = & 8.1087 \end{align} }[/math]
The corresponding current demonstrated failure intensity is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{D}}= & \frac{1}{MTB{{F}_{D}}} \\ & = & 0.1233 \end{align} }[/math]
- 2) The average nominal effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average Nominal EF):
- [math]\displaystyle{ \begin{align} & {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ & = & \frac{0.67+0.72+0.77+0.77+0.87+0.92+0.5+0.74+0.7+0.63+0.64+0.46}{12} \\ & = & 0.6992 \end{align} }[/math]
The average actual effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average actual EF):
- [math]\displaystyle{ \begin{align} & {{d}_{A}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M} \\ & = & \frac{0.67+0+0.77+0+0.87+0+0+0.74+0+0+0.64+0}{12} \\ & = & 0.3075 \end{align} }[/math]
- 3) The [math]\displaystyle{ p }[/math] ratio is calculated by using Eqn. (p ratio):
- [math]\displaystyle{ \begin{align} & p= & \frac{\text{Total number of distinct unfixed BD modes at time }400}{\text{Total number of distinct BD modes at time }400\text{ (both fixed and unfixed)}} \\ & = & \frac{12}{12+5} \\ & = & 0.7059 \end{align} }[/math]
- 4) The nominal growth potential factor is given by Eqn. (Nonimal GP Factor) :
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ni}} \right)\frac{{{N}_{i}}}{T} }[/math]
The total number [math]\displaystyle{ M }[/math] of distinct unfixed BD modes at time [math]\displaystyle{ 400 }[/math] is [math]\displaystyle{ M=12. }[/math]
- [math]\displaystyle{ {{d}_{Ni}} }[/math] is the assigned (nominal) EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}}, }[/math] (as given in Figure EF example 1).
- [math]\displaystyle{ {{N}_{i}} }[/math] is the total number of failures over (0, [math]\displaystyle{ 400 }[/math] ) for the distinct unfixed BD mode [math]\displaystyle{ i }[/math] . This is summarized in Table 10.3.
| Table 10.3 - Number of failures for unfixed BD modes | ||
| Classification | Mode | Number of Failures |
|---|---|---|
| BD | 2000 | 4 |
| BD | 3000 | 2 |
| BD | 4000 | 2 |
| BD | 5000 | 3 |
| BD | 6000 | 1 |
| BD | 7000 | 1 |
| BD | 8000 | 1 |
| BD | 11000 | 2 |
| BD | 12000 | 2 |
| BD | 13000 | 1 |
| BD | 14000 | 1 |
| BD | 17000 | 1 |
| Sum = 21 | ||
Based on the above, the nominal growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=0.0153 }[/math]
The actual growth potential factor is given by Eqn. (Actual GP factor):
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ai}} \right)\frac{{{N}_{i}}}{T} }[/math]
where [math]\displaystyle{ {{d}_{Ai}} }[/math] is the actual EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time 400, depending on whether a fix was implemented at time 400 or not. Figure Event report example 1 shows an event report from RGA 7 where it can be seen that the actual EF is zero if a fix was not implemented at 400, or equal to the nominal EF if the fix was implemented at 400.
Based on the above, the actual growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=0.0344 }[/math]
- 5) The total number of unfixed BD modes is 21, based on Table 10.2. From Eqn. (lambdaBDunfixed), the unfixed BD mode failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- 6) The discovery rate parameters at time [math]\displaystyle{ 400 }[/math] are calculated using all the first occurrences of all the BD modes, both fixed and unfixed. [math]\displaystyle{ {{\widehat{\beta }}_{BD}} }[/math] is the unbiased estimated of [math]\displaystyle{ \beta }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes in our example. [math]\displaystyle{ {{\widehat{\lambda }}_{BD}} }[/math] is the unbiased estimate of [math]\displaystyle{ \lambda }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the [math]\displaystyle{ 17 }[/math] distinct BD modes. Figure first occurence BD shows the first time to failure for each of the 17 distinct modes and the results of the analysis using the Crow-AMSAA (NHPP) model in RGA 7 (note that the calculation settings in the User Setup have to be set to calculate unbiased [math]\displaystyle{ \beta }[/math] in this case).
So we have:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6055 }[/math]
- and:
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.4518 }[/math]
The equations used to determine these parameters have been explained in question 1 of this example and are also presented in detail in Chapter 5, Section 5.1.1.
Based on Eqn. (Discovery Function), the discovery rate function at time 400 is:
- [math]\displaystyle{ \begin{align} & \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & 0.4518\cdot 0.6055\cdot {{400}^{0.6055-1}} \\ & = & 0.0257 \end{align} }[/math]
This is the failure intensity of the unseen BD modes at time 400. In this case, it means that 0.0257 new BD modes are discovered per hour, or one new BD mode is discovered every 38.9 hours.
Based on Eqn. (Nominal Growth Potential failure intensity), the nominal growth potential failure intensity is:
This is the minimum attainable failure intensity if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
From Eqn. (Nominal Growth Potential MTBF), the nominal growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NGP}}= & \frac{1}{{{\lambda }_{NGP}}} \\ & = & \frac{1}{0.080} \\ & = & 12.37 \end{align} }[/math]
This is the maximum attainable MTBF if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
- 8) From Eqn. (Nominal projected failure intensity), the nominal projected failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{NP}}= & {{\lambda }_{NGP}}+{{d}_{N}}h(400) \\ & = & 0.080+0.6992\cdot 0.0257 \\ & = & 0.0988 \end{align} }[/math]
This is the projected failure intensity assuming all delayed fixes have been implemented for the modes that have been seen.
The nominal projected MTBF at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NP}}= & \frac{1}{{{\lambda }_{NP}}} \\ & = & \frac{1}{0.0988} \\ & = & 10.11 \end{align} }[/math]
This is the projected MTBF assuming all delayed fixes have been implemented for the modes that have been seen.
- 9) Based on Eqn. (Actual GP FI), the actual growth potential failure intensity is:
This is the minimum attainable failure intensity based on the current management strategy.
The actual growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AGP}}= & \frac{1}{{{\lambda }_{AGP}}} \\ & = & \frac{1}{0.1029} \\ & = & 9.71 \end{align} }[/math]
This is the maximum attainable MTBF based on the current management strategy.
- 10) From Eqn. (Actual projected FI), the actual projected failure intensity at time is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{AP}}= & {{\lambda }_{AGP}}+{{d}_{A}}\cdot h\left( 400 \right) \\ & = & 0.1029+0.3075\cdot 0.0257 \\ & = & 0.1108 \end{align} }[/math]
This is the projected failure intensity based on the current management strategy.
The actual projected MTBF at time is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AP}}= & \frac{1}{{{\lambda }_{AP}}} \\ & = & \frac{1}{0.1108} \\ & = & 9.01 \end{align} }[/math]
This is the projected MTBF based on the current management strategy.
Figure QCP MTBFac demonstrates how we can derive the results of this example by using RGA 7's Quick Calculation Pad (QCP). Here we chose to calculate the actual projected MTBF.
Example 2
The Crow Extended - Continuous Evaluation model allows data analysis across multiple phases, up to seven individual phases. Figure Example2table, 6 phases shows a portion of failure time test results obtained across six phases. Analysis points are specified for continuous evaluation every 1000 hours. The cumulative test times at the end of each test phase are 5000, 15000, 25000, 35000, 45000 and 60000 hours.
Figure EFxample2 shows the effectiveness factors for the BD modes that do not have an associated fix implementation event. In other words, these are unfixed BD modes. Note that this specifies the phase after which the BD mode will be fixed, if any.
[math]\displaystyle{ }[/math]
Figure Example2Plot shows the overall test results in terms of demonstrated, projected and growth potential MTBF.
[math]\displaystyle{ }[/math]
Figure Indivdual Mode MTBF shows the Before and After MTBFs for all the individual modes. Note that the After MTBFs are calculated by taking into account the respective effectiveness factors for each of the unfixed BD modes.
[math]\displaystyle{ }[/math]
The analysis points are used to track overall growth inside and across phases, at desired intervals. A multi-phase plot can be created by right-clicking Additional Plots in the Project Explorer and selecting Add MultiPhase Plot. The MultiPhase Plot Wizard guides you through the process concerning the data sheet selection. Since the Crow Extended - Continuous Evaluation was used for the six-phase test, we select the Multi-Phase option.
A Multi-Phase data sheet can be associated with the multi-phase plot. Also, if there is an existing Planning folio, the multi-phase plot can bring the test results together with the Planning. This allows you to track the overall reliability program against the goals and set plans at each stage of the test. Additional information on combining a Planning folio and a MultiPhase plot is presented in Chapter 11.
Figure Multi-phase plot shows the multi-phase plot for the six phases of the reliability growth test program. This plot can be a powerful tool for overall tracking of the reliability growth program. It displays the termination time for each phase of testing along with the demonstrated, projected and growth potential MTBFs at those times. The plot also displays these calculated MTBFs at specified analysis points, which are determined based on the "AP" events in the data sheet.
[math]\displaystyle{ }[/math]
Template loop detected: Template:Discrete data crow rga
Template loop detected: Template:Statistical tests for effectiveness of corrective actions crow rga
As discussed in the previous chapter, the Crow Extended model is designed for a single test phase. However, in most cases testing for a system will be conducted in multiple phases. The Crow Extended - Continuous Evaluation model is designed for analyzing data across multiple test phases, while considering the data for all phases as one data set. In the RGA software, it is applied when using the Multi-Phase data sheet.
The Crow Extended - Continuous Evaluation (3-parameter) model is an extension of the Crow Extended model, and is designed for the practical testing situation where we need the flexibility to apply corrective actions at the time of failure or at a later time during the test, at the end of the current test or during a subsequent test phase. This three-parameter model is free of the constraint that testing must be stopped and all BD modes must be corrected at the end of the test, as in the Crow Extended model. The failure modes can be corrected during the test or when the testing is stopped for the incorporation of the fixes, or even not corrected at all at the end of the test phase. Based on this flexibility, the end time of testing is also not predefined, and it can be continuously updated with new test data, and this is the reason behind the naming, continuous evaluation.
Definitions
Template loop detected: Template:Classifications crow rga Template loop detected: Template:Event codes crow rga
Template loop detected: Template:P ratio crow rga
Template loop detected: Template:Effectiveness factor crow rga
Template loop detected: Template:Growth potential and projections crow rga
Example 1
Table 10.2 shows the Multi-Phase data with failure and fix implementation events. Figure Example 1 data in RGA 7 shows the Table 10.2 data as entered in RGA 7. Note that since this is a time terminated test with a single phase ending at [math]\displaystyle{ T=400 }[/math] , the last event entry is a phase (PH) with time to event = 400.
| Table 10.2 - Multi-Phase data for a time terminated test at [math]\displaystyle{ T=400 }[/math] | ||||||||
| Event | Time to Event | Classification | Mode | Event | Time to Event | Classification | Mode | |
|---|---|---|---|---|---|---|---|---|
| F | 0.7 | BD | 1000 | F | 244.8 | A | 3 | |
| F | 15 | BD | 2000 | F | 249 | BD | 13000 | |
| F | 17.6 | BC | 200 | F | 250.8 | A | 2 | |
| F | 25.3 | BD | 3000 | F | 260.1 | BD | 2000 | |
| F | 47.5 | BD | 4000 | F | 273.1 | A | 5 | |
| I | 50 | BD | 1000 | F | 274.7 | BD | 11000 | |
| F | 54 | BD | 5000 | I | 280 | BD | 9000 | |
| F | 54.5 | BC | 300 | F | 282.8 | BC | 902 | |
| F | 56.4 | BD | 6000 | F | 285 | BD | 14000 | |
| F | 63.6 | A | 1 | F | 315.4 | BD | 4000 | |
| F | 72.2 | BD | 5000 | F | 317.1 | A | 3 | |
| F | 99.2 | BC | 400 | F | 320.6 | A | 1 | |
| F | 99.6 | BD | 7000 | F | 324.5 | BD | 12000 | |
| F | 100.3 | BD | 8000 | F | 324.9 | BD | 10000 | |
| F | 102.5 | A | 2 | F | 342 | BD | 5000 | |
| F | 112 | BD | 9000 | F | 350.2 | BD | 3000 | |
| F | 112.2 | BC | 500 | F | 355.2 | BC | 903 | |
| F | 120.9 | BD | 2000 | F | 364.6 | BD | 10000 | |
| F | 121.9 | BC | 600 | F | 364.9 | A | 1 | |
| F | 125.5 | BD | 10000 | I | 365 | BD | 10000 | |
| F | 133.4 | BD | 11000 | F | 366.3 | BD | 2000 | |
| F | 151 | BC | 700 | F | 379.4 | BD | 15000 | |
| F | 163 | BC | 800 | F | 389 | BD | 16000 | |
| F | 174.5 | BC | 900 | I | 390 | BD | 15000 | |
| F | 177.4 | BD | 10000 | I | 393 | BD | 16000 | |
| F | 191.6 | BC | 901 | F | 394.9 | A | 3 | |
| F | 192.7 | BD | 12000 | F | 395.2 | BD | 17000 | |
| F | 213 | A | 1 | |||||
Figure EF example 1 shows the effectiveness factors for the unfixed BD modes and information concerning whether the fix will be implemented. Since we have only one test phase for this example, a 1 indicates that the fix will be implemented at the end of the first (and only) phase.
Do the following:
- 1) Determine the current demonstrated MTBF and failure intensity at time [math]\displaystyle{ T }[/math] .
- 2) Determine the nominal and actual average effectiveness factor at time [math]\displaystyle{ T }[/math] .
- 3) Determine the ratio.
- 4) Determine the nominal and actual growth potential factor.
- 5) Determine the unfixed BD mode failure intensity at time [math]\displaystyle{ T. }[/math]
- 6) Determine the rate of discovery parameters and the rate of discovery function at time [math]\displaystyle{ T }[/math] .
- 7) Determine the nominal growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 8) Determine the nominal projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 9) Determine the actual growth potential failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
- 10) Determine the actual projected failure intensity and MTBF at time [math]\displaystyle{ T. }[/math]
Solution
- 1) As seen in Chapter 5, for a time terminated test, [math]\displaystyle{ \beta }[/math] is estimated by the following equation:
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
where in this case [math]\displaystyle{ {{T}^{*}}= }[/math] termination time [math]\displaystyle{ =400, }[/math] and [math]\displaystyle{ n }[/math] is the total number of failures. In this example [math]\displaystyle{ n=50 }[/math] . Note that there are five fix implementation events and one event that marks the end of the phase. These should not be counted as failures.
So in this case we find that [math]\displaystyle{ \beta =0.9866. }[/math]
Note that here we calculated the biased estimate of [math]\displaystyle{ \beta }[/math] but we could have used the unbiased estimate as presented in Chapter 5. The choice of calculating the biased or unbiased estimate of [math]\displaystyle{ \beta }[/math] can be set in the User Setup in RGA 7.
Then solve for [math]\displaystyle{ \lambda , }[/math] based on the Crow-AMSAA (NHPP) equation explained in Chapter 5, Section 5.1.1:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{n}{{{T}^{*\beta }}} \\ & = & \frac{50}{{{400}^{0.9866}}} \\ & = & 0.1354 \end{align} }[/math]
The demonstrated MTBF of the system at time [math]\displaystyle{ T=400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{D}}= & \frac{1}{\lambda \beta {{T}^{\beta -1}}} \\ & = & 8.1087 \end{align} }[/math]
The corresponding current demonstrated failure intensity is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{D}}= & \frac{1}{MTB{{F}_{D}}} \\ & = & 0.1233 \end{align} }[/math]
- 2) The average nominal effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average Nominal EF):
- [math]\displaystyle{ \begin{align} & {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ & = & \frac{0.67+0.72+0.77+0.77+0.87+0.92+0.5+0.74+0.7+0.63+0.64+0.46}{12} \\ & = & 0.6992 \end{align} }[/math]
The average actual effectiveness factor at time [math]\displaystyle{ T }[/math] is given by Eqn. (Average actual EF):
- [math]\displaystyle{ \begin{align} & {{d}_{A}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M} \\ & = & \frac{0.67+0+0.77+0+0.87+0+0+0.74+0+0+0.64+0}{12} \\ & = & 0.3075 \end{align} }[/math]
- 3) The [math]\displaystyle{ p }[/math] ratio is calculated by using Eqn. (p ratio):
- [math]\displaystyle{ \begin{align} & p= & \frac{\text{Total number of distinct unfixed BD modes at time }400}{\text{Total number of distinct BD modes at time }400\text{ (both fixed and unfixed)}} \\ & = & \frac{12}{12+5} \\ & = & 0.7059 \end{align} }[/math]
- 4) The nominal growth potential factor is given by Eqn. (Nonimal GP Factor) :
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ni}} \right)\frac{{{N}_{i}}}{T} }[/math]
The total number [math]\displaystyle{ M }[/math] of distinct unfixed BD modes at time [math]\displaystyle{ 400 }[/math] is [math]\displaystyle{ M=12. }[/math]
- [math]\displaystyle{ {{d}_{Ni}} }[/math] is the assigned (nominal) EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}}, }[/math] (as given in Figure EF example 1).
- [math]\displaystyle{ {{N}_{i}} }[/math] is the total number of failures over (0, [math]\displaystyle{ 400 }[/math] ) for the distinct unfixed BD mode [math]\displaystyle{ i }[/math] . This is summarized in Table 10.3.
| Table 10.3 - Number of failures for unfixed BD modes | ||
| Classification | Mode | Number of Failures |
|---|---|---|
| BD | 2000 | 4 |
| BD | 3000 | 2 |
| BD | 4000 | 2 |
| BD | 5000 | 3 |
| BD | 6000 | 1 |
| BD | 7000 | 1 |
| BD | 8000 | 1 |
| BD | 11000 | 2 |
| BD | 12000 | 2 |
| BD | 13000 | 1 |
| BD | 14000 | 1 |
| BD | 17000 | 1 |
| Sum = 21 | ||
Based on the above, the nominal growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=0.0153 }[/math]
The actual growth potential factor is given by Eqn. (Actual GP factor):
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ai}} \right)\frac{{{N}_{i}}}{T} }[/math]
where [math]\displaystyle{ {{d}_{Ai}} }[/math] is the actual EF for the [math]\displaystyle{ {{i}^{th}} }[/math] unfixed BD mode at time 400, depending on whether a fix was implemented at time 400 or not. Figure Event report example 1 shows an event report from RGA 7 where it can be seen that the actual EF is zero if a fix was not implemented at 400, or equal to the nominal EF if the fix was implemented at 400.
Based on the above, the actual growth potential factor is calculated as:
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=0.0344 }[/math]
- 5) The total number of unfixed BD modes is 21, based on Table 10.2. From Eqn. (lambdaBDunfixed), the unfixed BD mode failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- 6) The discovery rate parameters at time [math]\displaystyle{ 400 }[/math] are calculated using all the first occurrences of all the BD modes, both fixed and unfixed. [math]\displaystyle{ {{\widehat{\beta }}_{BD}} }[/math] is the unbiased estimated of [math]\displaystyle{ \beta }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes in our example. [math]\displaystyle{ {{\widehat{\lambda }}_{BD}} }[/math] is the unbiased estimate of [math]\displaystyle{ \lambda }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the [math]\displaystyle{ 17 }[/math] distinct BD modes. Figure first occurence BD shows the first time to failure for each of the 17 distinct modes and the results of the analysis using the Crow-AMSAA (NHPP) model in RGA 7 (note that the calculation settings in the User Setup have to be set to calculate unbiased [math]\displaystyle{ \beta }[/math] in this case).
So we have:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6055 }[/math]
- and:
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.4518 }[/math]
The equations used to determine these parameters have been explained in question 1 of this example and are also presented in detail in Chapter 5, Section 5.1.1.
Based on Eqn. (Discovery Function), the discovery rate function at time 400 is:
- [math]\displaystyle{ \begin{align} & \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & 0.4518\cdot 0.6055\cdot {{400}^{0.6055-1}} \\ & = & 0.0257 \end{align} }[/math]
This is the failure intensity of the unseen BD modes at time 400. In this case, it means that 0.0257 new BD modes are discovered per hour, or one new BD mode is discovered every 38.9 hours.
Based on Eqn. (Nominal Growth Potential failure intensity), the nominal growth potential failure intensity is:
This is the minimum attainable failure intensity if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
From Eqn. (Nominal Growth Potential MTBF), the nominal growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NGP}}= & \frac{1}{{{\lambda }_{NGP}}} \\ & = & \frac{1}{0.080} \\ & = & 12.37 \end{align} }[/math]
This is the maximum attainable MTBF if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
- 8) From Eqn. (Nominal projected failure intensity), the nominal projected failure intensity at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{NP}}= & {{\lambda }_{NGP}}+{{d}_{N}}h(400) \\ & = & 0.080+0.6992\cdot 0.0257 \\ & = & 0.0988 \end{align} }[/math]
This is the projected failure intensity assuming all delayed fixes have been implemented for the modes that have been seen.
The nominal projected MTBF at time [math]\displaystyle{ 400 }[/math] is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{NP}}= & \frac{1}{{{\lambda }_{NP}}} \\ & = & \frac{1}{0.0988} \\ & = & 10.11 \end{align} }[/math]
This is the projected MTBF assuming all delayed fixes have been implemented for the modes that have been seen.
- 9) Based on Eqn. (Actual GP FI), the actual growth potential failure intensity is:
This is the minimum attainable failure intensity based on the current management strategy.
The actual growth potential MTBF is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AGP}}= & \frac{1}{{{\lambda }_{AGP}}} \\ & = & \frac{1}{0.1029} \\ & = & 9.71 \end{align} }[/math]
This is the maximum attainable MTBF based on the current management strategy.
- 10) From Eqn. (Actual projected FI), the actual projected failure intensity at time is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{AP}}= & {{\lambda }_{AGP}}+{{d}_{A}}\cdot h\left( 400 \right) \\ & = & 0.1029+0.3075\cdot 0.0257 \\ & = & 0.1108 \end{align} }[/math]
This is the projected failure intensity based on the current management strategy.
The actual projected MTBF at time is:
- [math]\displaystyle{ \begin{align} & MTB{{F}_{AP}}= & \frac{1}{{{\lambda }_{AP}}} \\ & = & \frac{1}{0.1108} \\ & = & 9.01 \end{align} }[/math]
This is the projected MTBF based on the current management strategy.
Figure QCP MTBFac demonstrates how we can derive the results of this example by using RGA 7's Quick Calculation Pad (QCP). Here we chose to calculate the actual projected MTBF.
Example 2
The Crow Extended - Continuous Evaluation model allows data analysis across multiple phases, up to seven individual phases. Figure Example2table, 6 phases shows a portion of failure time test results obtained across six phases. Analysis points are specified for continuous evaluation every 1000 hours. The cumulative test times at the end of each test phase are 5000, 15000, 25000, 35000, 45000 and 60000 hours.
Figure EFxample2 shows the effectiveness factors for the BD modes that do not have an associated fix implementation event. In other words, these are unfixed BD modes. Note that this specifies the phase after which the BD mode will be fixed, if any.
[math]\displaystyle{ }[/math]
Figure Example2Plot shows the overall test results in terms of demonstrated, projected and growth potential MTBF.
[math]\displaystyle{ }[/math]
Figure Indivdual Mode MTBF shows the Before and After MTBFs for all the individual modes. Note that the After MTBFs are calculated by taking into account the respective effectiveness factors for each of the unfixed BD modes.
[math]\displaystyle{ }[/math]
The analysis points are used to track overall growth inside and across phases, at desired intervals. A multi-phase plot can be created by right-clicking Additional Plots in the Project Explorer and selecting Add MultiPhase Plot. The MultiPhase Plot Wizard guides you through the process concerning the data sheet selection. Since the Crow Extended - Continuous Evaluation was used for the six-phase test, we select the Multi-Phase option.
A Multi-Phase data sheet can be associated with the multi-phase plot. Also, if there is an existing Planning folio, the multi-phase plot can bring the test results together with the Planning. This allows you to track the overall reliability program against the goals and set plans at each stage of the test. Additional information on combining a Planning folio and a MultiPhase plot is presented in Chapter 11.
Figure Multi-phase plot shows the multi-phase plot for the six phases of the reliability growth test program. This plot can be a powerful tool for overall tracking of the reliability growth program. It displays the termination time for each phase of testing along with the demonstrated, projected and growth potential MTBFs at those times. The plot also displays these calculated MTBFs at specified analysis points, which are determined based on the "AP" events in the data sheet.
[math]\displaystyle{ }[/math]
Template loop detected: Template:Discrete data crow rga
Template loop detected: Template:Statistical tests for effectiveness of corrective actions crow rga