Sequential Data - Logistic Model

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.

---

This example appears in the Reliability growth reference.

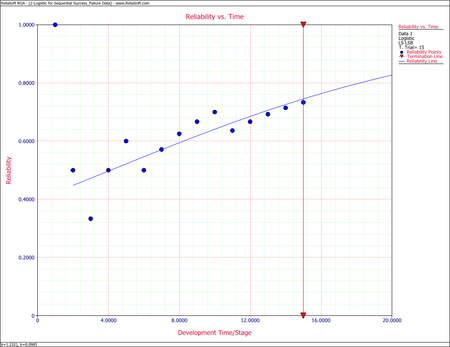
A prototype was tested under a success/failure pattern. The test consisted of 15 runs. The following table presents the data from the test. Find the Logistic model that best fits the data set, and plot it along with the reliability observed from the raw data.

Sequential Success/Failure Data with Observed Reliability Values

Time	Result	Observed Reliability
0	F	0.5000
1	F	0.3333
2	S	0.5000
3	S	0.6000
4	F	0.5000
5	S	0.5714
6	S	0.6250
7	S	0.6667
8	S	0.7000
9	F	0.6364
10	S	0.6667
11	S	0.6923
12	S	0.7143
13	S	0.7333

Solution

The first run is ignored because it was a success, and the reliability at that point was 100%. This failure will be ignored throughout the analysis because it is considered that the test starts when the reliability is not equal to zero or one. The test essentially begins at time 1, and is now considered as time 0 with [math]\displaystyle{ N=14\,\! }[/math]. The observed reliability is shown in the last column of the table. Keep in mind that the observed reliability values still account for the initial suspension.

Therefore:

[math]\displaystyle{ \begin{align} \bar{Y}= & \frac{1}{N}\underset{i=0}{\overset{N-1}{\mathop \sum }}\,{{Y}_{i}} \\ = & \frac{1}{14}\underset{i=0}{\overset{13}{\mathop \sum }}\,\ln \left( \frac{1}{{{R}_{i}}}-1 \right) \\ = & -0.43163 \end{align}\,\! }[/math]

and:

[math]\displaystyle{ \begin{align} \bar{T}= & \frac{1}{14}\underset{i=0}{\overset{13}{\mathop \sum }}\,{{T}_{i}} \\ = & 6.5 \\ \underset{i=0}{\overset{13}{\mathop \sum }}\,T_{i}^{2}= & 819.0 \\ \underset{i=0}{\overset{13}{\mathop \sum }}\,{{T}_{i}}{{Y}_{i}}= & -61.69 \end{align}\,\! }[/math]

Now, from the least squares estimators, the values are:

[math]\displaystyle{ \begin{align} {{{\hat{b}}}_{1}}&= \frac{\underset{i=0}{\overset{N-1}{\mathop{\sum }}}\,{{T}_{i}}{{Y}_{i}}-N\cdot \bar{T}\cdot \bar{Y}}{\underset{i=0}{\overset{N-1}{\mathop{\sum }}}\,T_{i}^{2}-N\cdot {{{\bar{T}}}^{2}}} \\ \\ &= \frac{-61.69-14 \cdot 6.5 \cdot (-.43163)}{819.0-14 \cdot 6.5^{2}} \\ &= -0.0985 \\ \\ \hat{b_{0}}&= \overline{Y} - \hat{b_{1}}\overline{T} \\ &= (-.043163)-(-0.0985) \cdot 6.5 \\ &= 0.2087 \end{align}\,\! }[/math]

Therefore:

[math]\displaystyle{ \begin{align} \widehat{b}= & {{e}^{0.2087}} \\ = & 1.2321 \\ \widehat{k}= & -(-0.0985) \\ = & 0.0985 \end{align}\,\! }[/math]

The Logistic reliability model that best fits the data is given by:

[math]\displaystyle{ R=\frac{1}{1+1.2321\cdot \ \,{{e}^{-0.0985T}}}\,\! }[/math]

The following figure shows the Reliability vs. Time plot.