New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at DOE examples and DOE reference examples.
|
Central Composite Response Surface Method
|
This example validates the calculation of the central composite response surface method in Weibull++.
Reference Case
The data are from Example 11-1 on page 431 in the book Design and Analysis of Experiments by Douglas C. Montgomery, John Wiley & Sons, 2001.
Data
| Natural Variables
|
Coded Variables
|
Responses
|
| A (time)
|
B (temperature)
|
A
|
B
|
Y (yield)
|
| 8076.580 |
170 |
-1 |
-1 |
76.5
|
| 80 |
180 |
-1 |
1 |
77
|
| 90 |
170 |
1 |
-1 |
78
|
| 90 |
180 |
1 |
1 |
79.5
|
| 85 |
175 |
0 |
0 |
79.9
|
| 85 |
175 |
0 |
0 |
80.3
|
| 85 |
175 |
0 |
0 |
80.0
|
| 85 |
175 |
0 |
0 |
79.7
|
| 85 |
175 |
0 |
0 |
79.8
|
| 92.07 |
175 |
1.414 |
0 |
78.4
|
| 77.93 |
175 |
-1.414 |
0 |
75.6
|
| 85 |
182.07 |
0 |
1.414 |
78.5
|
| 85 |
167.93 |
0 |
-1.414 |
77
|
Result
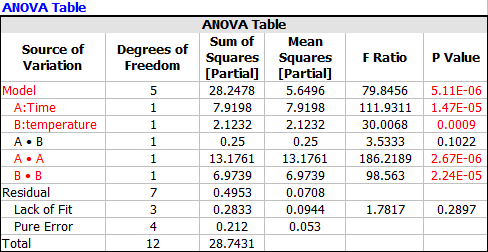
From the book, the ANOVA table is:
| Source
|
Sum of Squares (Partial SS)
|
DF
|
Mean Square
|
F value
|
Prob > F
|
| Model |
28.25 |
5 |
5.65 |
79.85 |
<0.0001
|
| A |
7.92 |
1 |
7.92 |
111.93 |
<0.0001
|
| B |
2.12 |
1 |
2.12 |
30.01 |
0.0009
|
| A∙A |
13.18 |
1 |
13.18 |
186.22 |
<0.0001
|
| B∙B |
6.97 |
1 |
6.97 |
98.56 |
<0.0001
|
| A∙B |
0.25 |
1 |
0.25 |
3.53 |
0.1022
|
| Residual |
0.5 |
7 |
0.071 |
|
|
| Lack of Fit |
0.28 |
3 |
0.094 |
1.78 |
0.2897
|
| Pure Error |
0.21 |
4 |
0.053 |
|
|
| Total |
28.74 |
12 |
|
|
|
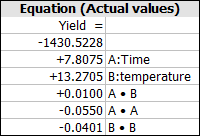
The final equation in terms of the actual values of these two factors is:
- [math]\displaystyle{ \begin{align}
Yield= -1430.52285+7.80749 * time + 13.27053 * temp-0.05505 * time^2 - 0.04005 * temp^2 + 0.01 * time * temp
\end{align} }[/math]
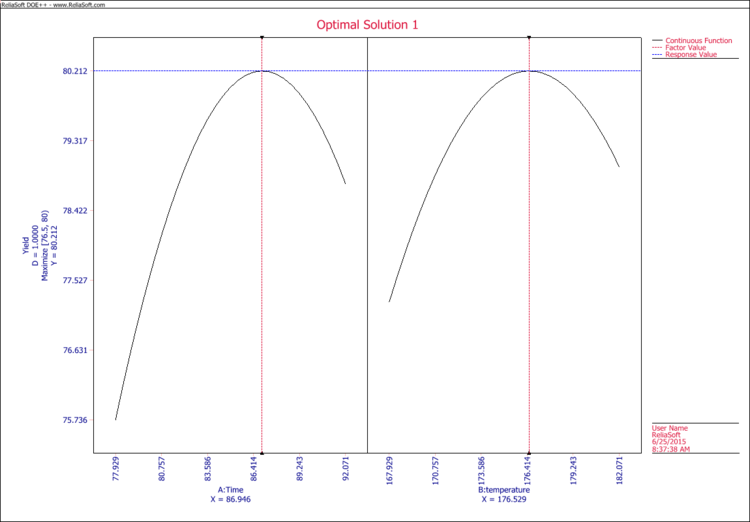
The maximum yield is achieved at 80.21 with time = 87 minutes and temperature = 176.5 F.
Results in DOE++
The software results match the book results. The ANOVA table is:
The final equation in terms of the actual factors is:
The maximum yield is achieved at 80.21, as shown in the optimization plot. The values at the red dash line are the optimal values for factor A and factor B. The blue line corresponds to the maximum Y value.