Standby Configuration Example
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at BlockSim examples and BlockSim reference examples.
This example appears in the System analysis reference.
Consider a car with four new tires and a full-size spare. Assume the following failure characteristics:
- The tires follow a Weibull distribution with a [math]\displaystyle{ \beta=4\,\! }[/math] and an [math]\displaystyle{ \eta = 40,000\,\! }[/math] miles while on the car due to wear.
- The tires also have a probability of failing due to puncture or other causes. For this, assume a constant rate for this occurrence with a probability of 1 every 50,000 miles.
- When not on the car (i.e., is a spare), a tire's probability of failing also has a Weibull distribution with a [math]\displaystyle{ \beta = 2\,\! }[/math] and [math]\displaystyle{ \eta = 120,000\,\! }[/math] miles.
Assume a mission of 1,000 miles. If a tire fails during this trip, it will be replaced with the spare. However, the spare will not be repaired during the trip. In other words, the trip will continue with the spare on the car and, if the spare fails, the system will fail. Determine the probability of system failure.
Solution
The active failure distribution for the tires are:
- Due to wearout, Weibull [math]\displaystyle{ \beta =4\,\! }[/math] and [math]\displaystyle{ \eta =40,000\,\! }[/math] miles.
- Due to random puncture, exponential [math]\displaystyle{ \mu =50,000.\,\! }[/math]
- The quiescent failure distribution is a Weibull distribution with [math]\displaystyle{ \beta =2\,\! }[/math] and [math]\displaystyle{ \eta =120,000\,\! }[/math] miles.
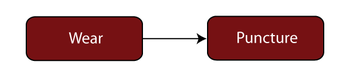
The block diagram for each tire has two blocks in series, one block representing the wearout mode and the other the random puncture mode, as shown next:
There are five tires, four active and one standby (represented in the diagram by a standby container with a 4-out-of-5 requirement), as shown next:
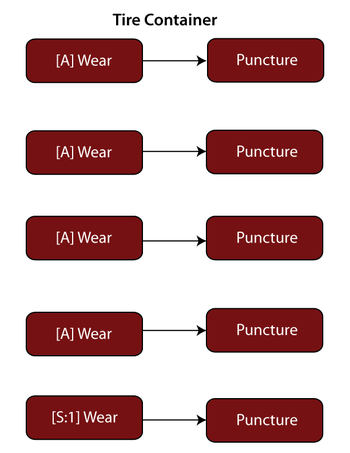
For the standby Wear block, set the active failure and the quiescent distributions, but for the Puncture block, set only the active puncture distribution (because the tire cannot fail due to puncture while stored). Using BlockSim, the probability of system failure is found to be 0.003 or 0.3%.
