Optimal Custom Design Example
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at DOE examples and DOE reference examples.
This example appears in the DOE reference.
Assume that we need to design an experiment to investigate five factors with two levels each. To run a full factorial design, a total of [math]\displaystyle{ {{2}^{5}}=32\,\! }[/math] factor combinations are needed. However, only 11 samples are available. To obtain the most information, which of the 11 factor combinations from the total of 32 should be applied to these 11 samples? To answer this question, we need to first decide what information we want to obtain.
The 32 runs required for a full factorial design are given in the table below.
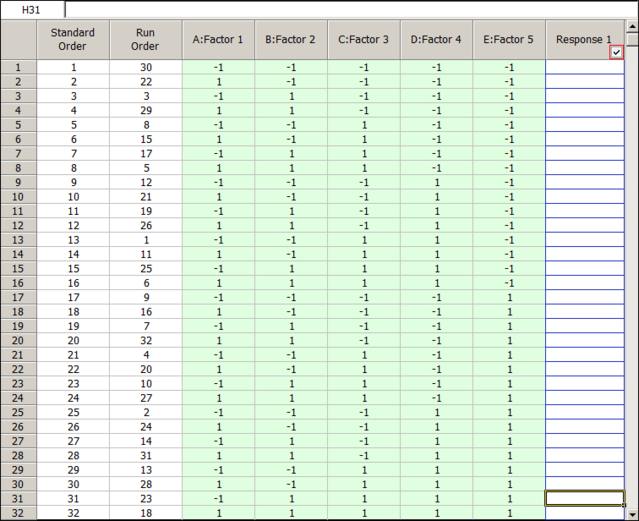
Order A B C D E 1 -1 -1 -1 -1 -1 2 1 -1 -1 -1 -1 3 -1 1 -1 -1 -1 4 1 1 -1 -1 -1 5 -1 -1 1 -1 -1 6 1 -1 1 -1 -1 7 -1 1 1 -1 -1 8 1 1 1 -1 -1 9 -1 -1 -1 1 -1 10 1 -1 -1 1 -1 11 -1 1 -1 1 -1 12 1 1 -1 1 -1 13 -1 -1 1 1 -1 14 1 -1 1 1 -1 15 -1 1 1 1 -1 16 1 1 1 1 -1 17 -1 -1 -1 -1 1 18 1 -1 -1 -1 1 19 -1 1 -1 -1 1 20 1 1 -1 -1 1 21 -1 -1 1 -1 1 22 1 -1 1 -1 1 23 -1 1 1 -1 1 24 1 1 1 -1 1 25 -1 -1 -1 1 1 26 1 -1 -1 1 1 27 -1 1 -1 1 1 28 1 1 -1 1 1 29 -1 -1 1 1 1 30 1 -1 1 1 1 31 -1 1 1 1 1 32 1 1 1 1 1
Since only 11 test samples are available, we must choose 11 factor value combinations from the above table. The experiment also has the following constraints:
• Due to safety concerns, it is not allowed to set all the factors at their high level at the same time. Therefore, we cannot use run number 32 in the experiment.
• The engineers are very interested in checking the response at A=D=1, and B=C=E=-1. Therefore, run number 10 must be included in the experiment.
• The engineers need to check the main effects and the interaction effect of AE. Therefore, the model for designing the optimal customer design is:
- [math]\displaystyle{ y={{\beta }_{0}}+{{\beta }_{1}}A+{{\beta }_{2}}B+{{\beta }_{3}}C+{{\beta }_{4}}D+{{\beta }_{5}}E+{{\beta }_{15}}AE+\varepsilon \,\! }[/math]
Since run number 10 must be included, there are only 10 runs left to choose from the above table. Many algorithms can be used to choose these 10 runs to maximize the determinant of the information matrix.
For this example, we first need to create a regular two level factorial design with five factors, as shown next.
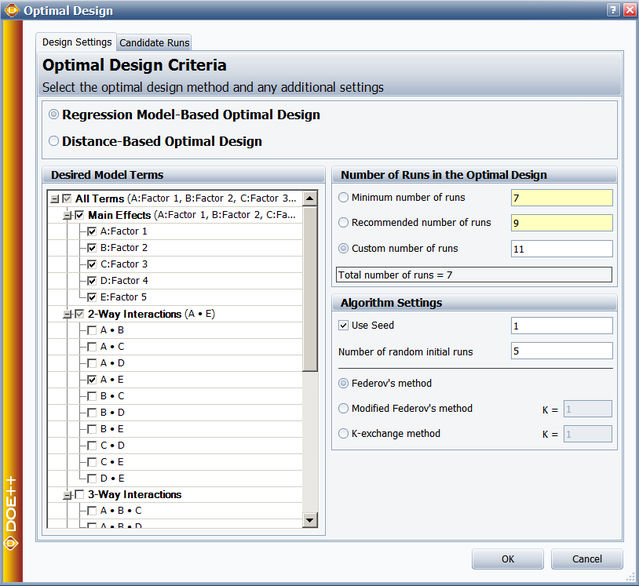
On the Design Settings tab of the Optimal Design window, you can select which terms to include in the model and specify the number of runs to be used in the experiment. Only main effects and AE are selected. The number of runs is set to 11. In the Candidate Runs tab of the window, run number 10 was set to be included and run number 32 was set to be excluded.
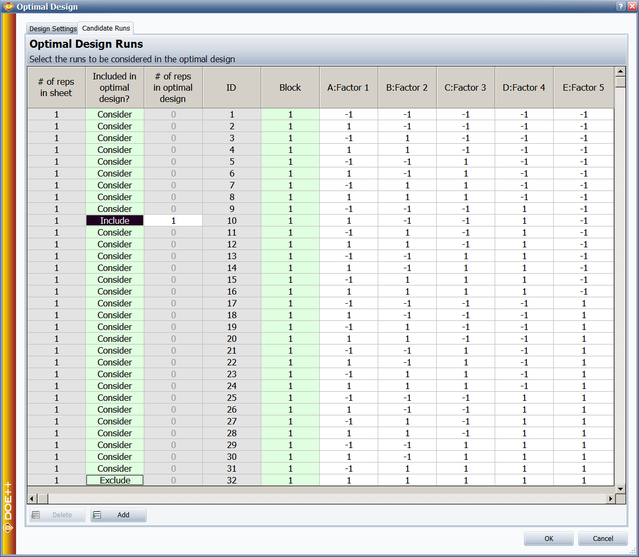
The resulting optimal custom design is shown next.
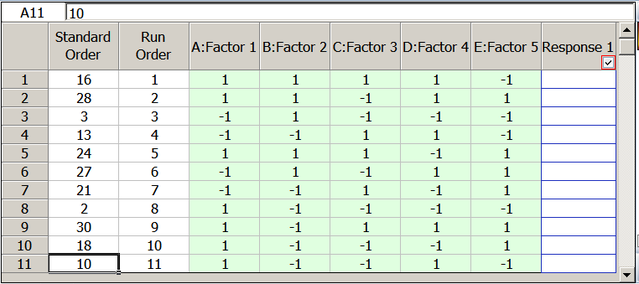
The design evaluation results for this design are given below.
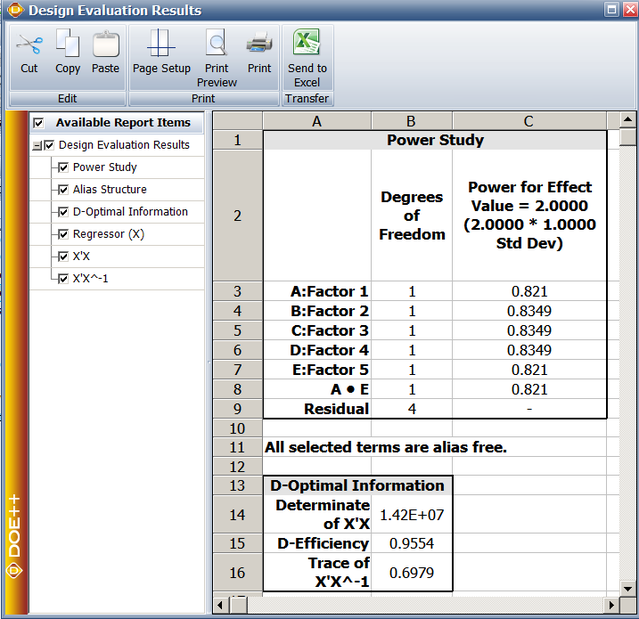
From the design evaluation results, we can see the generated design can clearly estimate all the main effects and the AE interaction. The determinate of the information matrix X’X is 1.42E+7 and the D-efficiency is 0.9554. The power for an effect of 2-standard deviation for each of the terms of interest is also given in the design evaluation.