New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example appears in the Life data analysis reference.
A health care company maintains five identical pieces of equipment used by a hospital. When a piece of equipment fails, the company sends a crew to repair it. The following table gives the failure and censoring ages for each machine, where the + sign indicates a censoring age.
[math]\displaystyle{ \begin{matrix}
Equipment ID & Months \\
\text{1} & \text{5, 10 , 15, 17+} \\
\text{2} & \text{6, 13, 17, 19+} \\
\text{3} & \text{12, 20, 25, 26+} \\
\text{4} & \text{13, 15, 24+} \\
\text{5} & \text{16, 22, 25, 28+} \\
\end{matrix}\,\! }[/math]
Estimate the MCF values, with 95% confidence bounds.
Solution
The MCF estimates are obtained as follows:
[math]\displaystyle{ \begin{matrix}
ID & Months ({{t}_{i}}) & State & {{r}_{i}} & 1/{{r}_{i}} & {{M}^{*}}({{t}_{i}}) \\
\text{1} & \text{5} & \text{F} & \text{5} & \text{0}\text{.20} & \text{0}\text{.20} \\
\text{2} & \text{6} & \text{F} & \text{5} & \text{0}\text{.20} & \text{0}\text{.20 + 0}\text{.20 = 0}\text{.40} \\
\text{1} & \text{10} & \text{F} & \text{5} & \text{0}\text{.20} & \text{0}\text{.40 + 0}\text{.20 = 0}\text{.60} \\
\text{3} & \text{12} & \text{F} & \text{5} & \text{0}\text{.20} & \text{0}\text{.60 + 0}\text{.20 = 0}\text{.80} \\
\text{2} & \text{13} & \text{F} & \text{5} & \text{0}\text{.20} & \text{0}\text{.80 + 0}\text{.20 = 1}\text{.00} \\
\text{4} & \text{13} & \text{F} & \text{5} & \text{0}\text{.20} & \text{1}\text{.00 + 0}\text{.20 = 1}\text{.20} \\
\text{1} & \text{15} & \text{F} & \text{5} & \text{0}\text{.20} & \text{1}\text{.20 + 0}\text{.20 = 1}\text{.40} \\
\text{4} & \text{15} & \text{F} & \text{5} & \text{0}\text{.20} & \text{1}\text{.40 + 0}\text{.20 = 1}\text{.60} \\
\text{5} & \text{16} & \text{F} & \text{5} & \text{0}\text{.20} & \text{1}\text{.60 + 0}\text{.20 = 1}\text{.80} \\
\text{2} & \text{17} & \text{F} & \text{5} & \text{0}\text{.20} & \text{1}\text{.80 + 0}\text{.20 = 2}\text{.00} \\
\text{1} & \text{17} & \text{S} & \text{4} & {} & {} \\
\text{2} & \text{19} & \text{S} & \text{3} & {} & {} \\
\text{3} & \text{20} & \text{F} & \text{3} & \text{0}\text{.33} & \text{2}\text{.00 + 0}\text{.33 = 2}\text{.33} \\
\text{5} & \text{22} & \text{F} & \text{3} & \text{0}\text{.33} & \text{2}\text{.33 + 0}\text{.33 = 2}\text{.66} \\
\text{4} & \text{24} & \text{S} & \text{2} & {} & {} \\
\text{3} & \text{25} & \text{F} & \text{2} & \text{0}\text{.50} & \text{2}\text{.66 + 0}\text{.50 = 3}\text{.16} \\
\text{5} & \text{25} & \text{F} & \text{2} & \text{0}\text{.50} & \text{3}\text{.16 + 0}\text{.50 = 3}\text{.66} \\
\text{3} & \text{26} & \text{S} & \text{1} & {} & {} \\
\text{5} & \text{28} & \text{S} & \text{0} & {} & {} \\
\end{matrix}\,\! }[/math]
Using the MCF variance equation, the following table of variance values can be obtained:
| ID
|
Months
|
State
|
[math]\displaystyle{ {{r}_{i}}\,\! }[/math]
|
[math]\displaystyle{ Va{{r}_{i}}\,\! }[/math]
|
| 1
|
5
|
F
|
5
|
[math]\displaystyle{ (\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.032\,\! }[/math]
|
| 2
|
6
|
F
|
5
|
[math]\displaystyle{ 0.032+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.064\,\! }[/math]
|
| 1
|
10
|
F
|
5
|
[math]\displaystyle{ 0.064+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.096\,\! }[/math]
|
| 3
|
12
|
F
|
5
|
[math]\displaystyle{ 0.096+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.128\,\! }[/math]
|
| 2
|
13
|
F
|
5
|
[math]\displaystyle{ 0.128+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.160\,\! }[/math]
|
| 4
|
13
|
F
|
5
|
[math]\displaystyle{ 0.160+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.192\,\! }[/math]
|
| 1
|
15
|
F
|
5
|
[math]\displaystyle{ 0.192+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.224\,\! }[/math]
|
| 4
|
15
|
F
|
5
|
[math]\displaystyle{ 0.224+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.256\,\! }[/math]
|
| 5
|
16
|
F
|
5
|
[math]\displaystyle{ 0.256+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.288\,\! }[/math]
|
| 2
|
17
|
F
|
5
|
[math]\displaystyle{ 0.288+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.320\,\! }[/math]
|
| 1
|
17
|
S
|
4
|
|
| 2
|
19
|
S
|
3
|
|
| 3
|
20
|
F
|
3
|
[math]\displaystyle{ 0.320+(\tfrac{1}{3})^2[(1-\tfrac{1}{3})^2+2(0-\tfrac{1}{3})^2]=0.394\,\! }[/math]
|
| 5
|
22
|
F
|
3
|
[math]\displaystyle{ 0.394+(\tfrac{1}{3})^2[(1-\tfrac{1}{3})^2+2(0-\tfrac{1}{3})^2]=0.468\,\! }[/math]
|
| 4
|
24
|
S
|
2
|
|
| 3
|
25
|
F
|
2
|
[math]\displaystyle{ 0.468+(\tfrac{1}{2})^2[(1-\tfrac{1}{2})^2+(0-\tfrac{1}{2})^2]=0.593\,\! }[/math]
|
| 5
|
25
|
F
|
2
|
[math]\displaystyle{ 0.593+(\tfrac{1}{2})^2[(1-\tfrac{1}{2})^2+(0-\tfrac{1}{2})^2]=0.718\,\! }[/math]
|
| 3
|
26
|
S
|
1
|
|
| 5
|
28
|
S
|
0
|
|
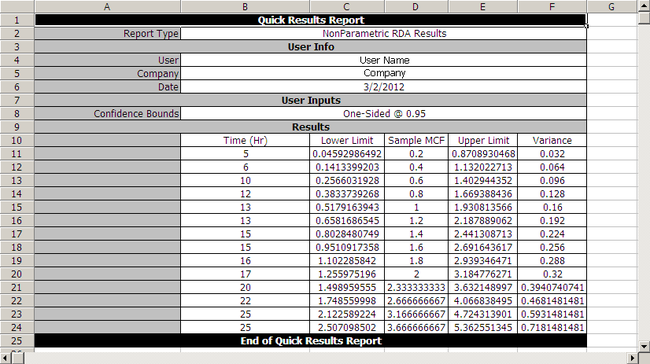
Using the equation for the MCF bounds and [math]\displaystyle{ {{K}_{5}} = 1.644\,\! }[/math] for a 95% confidence level, the confidence bounds can be obtained as follows:
[math]\displaystyle{ \begin{matrix}
ID & Months & State & MC{{F}_{i}} & Va{{r}_{i}} & MC{{F}_{{{L}_{i}}}} & MC{{F}_{{{U}_{i}}}} \\
\text{1} & \text{5} & \text{F} & \text{0}\text{.20} & \text{0}\text{.032} & 0.0459 & 0.8709 \\
\text{2} & \text{6} & \text{F} & \text{0}\text{.40} & \text{0}\text{.064} & 0.1413 & 1.1320 \\
\text{1} & \text{10} & \text{F} & \text{0}\text{.60} & \text{0}\text{.096} & 0.2566 & 1.4029 \\
\text{3} & \text{12} & \text{F} & \text{0}\text{.80} & \text{0}\text{.128} & 0.3834 & 1.6694 \\
\text{2} & \text{13} & \text{F} & \text{1}\text{.00} & \text{0}\text{.160} & 0.5179 & 1.9308 \\
\text{4} & \text{13} & \text{F} & \text{1}\text{.20} & \text{0}\text{.192} & 0.6582 & 2.1879 \\
\text{1} & \text{15} & \text{F} & \text{1}\text{.40} & \text{0}\text{.224} & 0.8028 & 2.4413 \\
\text{4} & \text{15} & \text{F} & \text{1}\text{.60} & \text{0}\text{.256} & 0.9511 & 2.6916 \\
\text{5} & \text{16} & \text{F} & \text{1}\text{.80} & \text{0}\text{.288} & 1.1023 & 2.9393 \\
\text{2} & \text{17} & \text{F} & \text{2}\text{.00} & \text{0}\text{.320} & 1.2560 & 3.1848 \\
\text{1} & \text{17} & \text{S} & {} & {} & {} & {} \\
\text{2} & \text{19} & \text{S} & {} & {} & {} & {} \\
\text{3} & \text{20} & \text{F} & \text{2}\text{.33} & \text{0}\text{.394} & 1.4990 & 3.6321 \\
\text{5} & \text{22} & \text{F} & \text{2}\text{.66} & \text{0}\text{.468} & 1.7486 & 4.0668 \\
\text{4} & \text{24} & \text{S} & {} & {} & {} & {} \\
\text{3} & \text{25} & \text{F} & \text{3}\text{.16} & \text{0}\text{.593} & 2.1226 & 4.7243 \\
\text{5} & \text{25} & \text{F} & \text{3}\text{.66} & \text{0}\text{.718} & 2.5071 & 5.3626 \\
\text{3} & \text{26} & \text{S} & {} & {} & {} & {} \\
\text{5} & \text{28} & \text{S} & {} & {} & {} & {} \\
\end{matrix}\,\! }[/math]
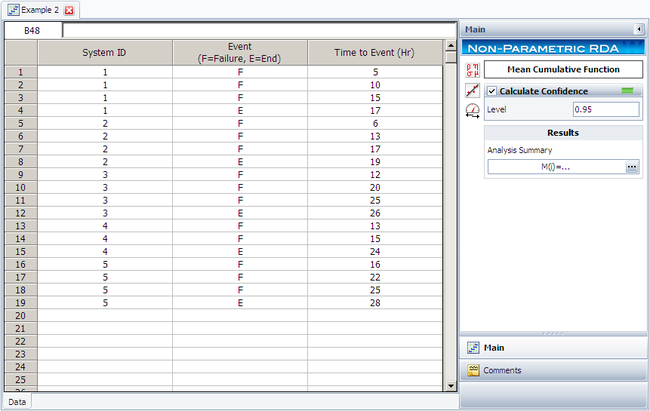
The analysis presented in this example can be performed automatically in Weibull++'s non-parametric RDA folio, as shown next.
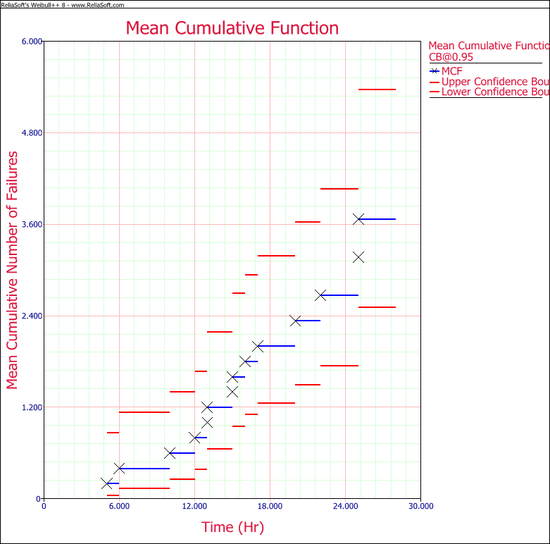
Note: In the folio above, the [math]\displaystyle{ F\,\! }[/math] refers to failures and [math]\displaystyle{ E\,\! }[/math] refers to suspensions (or censoring ages). The results, with calculated MCF values and upper and lower 95% confidence limits, are shown next along with the graphical plot.