Duane Model Examples
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
These examples appear in the Reliability growth reference.
Parameter Estimation Examples
Graphical Approach
A complex system's reliability growth is being monitored and the data set is given in the table below.
| Point Number | Cumulative Test Time(hours) | Cumulative Failures | Cumulative MTBF(hours) | Instantaneous MTBF(hours) |
|---|---|---|---|---|
| 1 | 200 | 2 | 100.0 | 100 |
| 2 | 400 | 3 | 133.0 | 200 |
| 3 | 600 | 4 | 150.0 | 200 |
| 4 | 3,000 | 11 | 273.0 | 342.8 |
Do the following:
- Plot the cumulative MTBF growth curve.
- Write the equation of this growth curve.
- Write the equation of the instantaneous MTBF growth model.
- Plot the instantaneous MTBF growth curve.
Solution
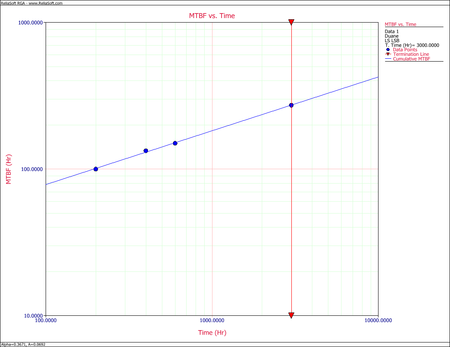
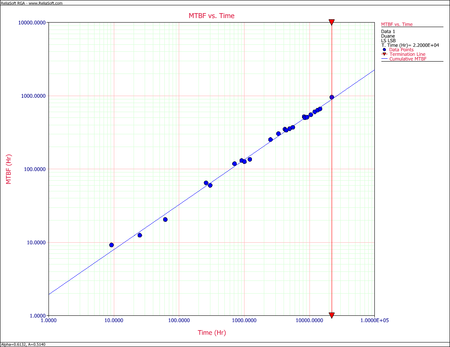
- Given the data in the second and third columns of the above table, the cumulative MTBF, [math]\displaystyle{ {{\hat{m}}_{c}}\,\! }[/math], values are calculated in the fourth column. The information in the second and fourth columns are then plotted. The first figure below shows the cumulative MTBF while the second figure below shows the instantaneous MTBF. It can be seen that a straight line represents the MTBF growth very well on log-log scales.
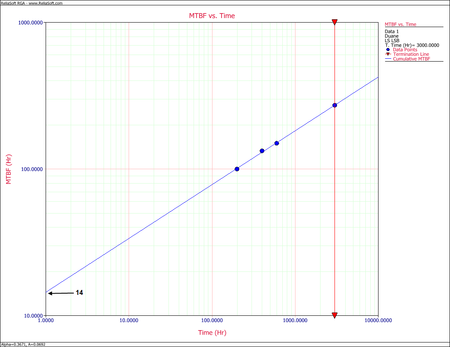
Cumulative MTBF plot Instantaneous MTBF plot By changing the x-axis scaling, you are able to extend the line to [math]\displaystyle{ T=1\,\! }[/math]. You can get the value of [math]\displaystyle{ b\,\! }[/math] from the graph by positioning the cursor at the point where the line meets the y-axis. Then read the value of the y-coordinate position at the bottom left corner. In this case, [math]\displaystyle{ b\,\! }[/math] is approximately 14 hours. The next figure illustrates this.
Cumulative MTBF plot for [math]\displaystyle{ b \approx 14\,\! }[/math] at [math]\displaystyle{ T=1\,\! }[/math] Another way of determining [math]\displaystyle{ b\,\! }[/math] is to calculate [math]\displaystyle{ \alpha \,\! }[/math] by using two points on the fitted straight line and substituting the corresponding [math]\displaystyle{ {{\hat{m}}_{c}}\,\! }[/math] and [math]\displaystyle{ T\,\! }[/math] values into:
- [math]\displaystyle{ \alpha =\frac{\ln \left( {{{\hat{m}}}_{{{c}_{2}}}} \right)-\ln \left( {{{\hat{m}}}_{{{c}_{1}}}} \right)}{\ln \left( {{T}_{_{2}}} \right)-\ln \left( {{T}_{_{1}}} \right)}\,\! }[/math]
Then substitute this [math]\displaystyle{ \alpha \,\! }[/math] and choose a set of values for [math]\displaystyle{ {{\hat{m}}_{{{c}_{1}}}}\,\! }[/math] and [math]\displaystyle{ {{T}_{_{1}}}\,\! }[/math] into the cumulative MTBF equation, [math]\displaystyle{ {{\hat{m}}_{c}}=b{{T}^{\alpha }}\,\! }[/math], and solve for [math]\displaystyle{ b\,\! }[/math]. The slope of the line, [math]\displaystyle{ \alpha \,\! }[/math], may also be found from the linearized form of the cumulative MTBF equation, or :
- [math]\displaystyle{ \alpha =\frac{\ln \left( {{{\hat{m}}}_{c}} \right)-\ln (b)}{\ln (T)-\ln (1)}\,\! }[/math]
Using the cumulative MTBF plot for the example, at [math]\displaystyle{ {{T}_{_{1}}}=200\,\! }[/math] hours, [math]\displaystyle{ {{\hat{m}}_{{{c}_{1}}}}=100\,\! }[/math] hours, and [math]\displaystyle{ {{T}_{_{2}}}=3,500\,\! }[/math] hours, [math]\displaystyle{ {{\hat{m}}_{{{c}_{2}}}}=300\,\! }[/math] hours. From the cumulative MTBF plot for [math]\displaystyle{ b=14\,\! }[/math] hours when [math]\displaystyle{ T=1\,\! }[/math], substituting the first set of values, [math]\displaystyle{ b=14\,\! }[/math] hours and [math]\displaystyle{ \ln 1=0\,\! }[/math], into the equation yields:
- [math]\displaystyle{ \begin{align} {{\alpha }_{1}}= & \frac{\ln (100)-\ln (14)}{\ln (200)-\ln (1)} \\ = & 0.3711 \end{align}\,\! }[/math]
- Substituting the second set of values, [math]\displaystyle{ b=14\,\! }[/math] hours and [math]\displaystyle{ \ln 1=0,\,\! }[/math] into the equation yields:
- [math]\displaystyle{ \begin{align} {{\alpha }_{2}}= & \frac{\ln (300)-\ln (14)}{\ln (3,500)-\ln (1)} \\ = & 0.3755 \end{align}\,\! }[/math]
- Now the equation for the cumulative MTBF growth curve is:
- [math]\displaystyle{ {{\hat{m}}_{c}}=14\cdot {{T}^{\text{ }0.3733}}\,\! }[/math]
- Using the following equation for the instantaneous MTBF, or
- [math]\displaystyle{ {{m}_{i}} = \frac{1}{1-\alpha }{{{\hat{m}}}_{c}},:\ \ \alpha \not{=}1 \,\! }[/math]
- [math]\displaystyle{ \begin{align} {{\hat{m}}_{i}}=\frac{1}{1-0.3733} \cdot {{14T}^{0.3733}} \end{align}\,\! }[/math]
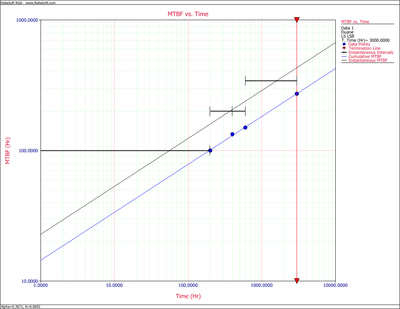
Cumulative and Instantaneous MTBF vs. Time plot
Mathematical Approach
Example 1
Using the same data set from the graphical approach example, estimate the parameters of the MTBF model using least squares.
Solution
From the data table:
- [math]\displaystyle{ \begin{align} \underset{i=1}{\overset{n}{\mathop \sum }}\,\ln ({{T}_{i}})&= & 25.693 \\ \underset{i=1}{\overset{n}{\mathop \sum }}\,\ln ({{T}_{i}})\ln ({{m}_{ci}})&= & 130.66 \\ \underset{i=1}{\overset{n}{\mathop \sum }}\,\ln ({{m}_{ci}})&= & 20.116 \\ \underset{i=1}{\overset{n}{\mathop \sum }}\,{{\left[ \ln ({{T}_{i}}) \right]}^{2}}&= & 168.99 \end{align}\,\! }[/math]
Obtain the value of [math]\displaystyle{ \hat{\alpha}\,\! }[/math] from the least squares analysis, or:
- [math]\displaystyle{ \begin{align} \hat{\alpha }&=\frac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}})\ln ({{m}_{ci}})-\tfrac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}})\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{m}_{ci}})}{n}}{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{\left[ \ln ({{T}_{i}}) \right]}^{2}}-\tfrac{{{\left( \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}}) \right)}^{2}}}{n}} \\ & = \frac{130.66-\tfrac{25.693\cdot 20.116}{4}}{168.99-\tfrac{{{25.693}^{2}}}{4}} \\ & = 0.3671 \end{align}\,\! }[/math]
Obtain the value [math]\displaystyle{ \hat{b}\,\! }[/math] from the least squares analysis, or:
- [math]\displaystyle{ \begin{align} \hat{b}&={{e}^{\tfrac{1}{n}\left[ \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{m}_{ci}})-\alpha \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}}) \right]}} \\ & = {{e}^{\tfrac{1}{4}(20.116-0.3671\cdot 25.693)}} \\ & = 14.456 \end{align}\,\! }[/math]
Therefore, the cumulative MTBF becomes:
- [math]\displaystyle{ \begin{align} \hat{m_{c}}&=bT^{\alpha } \\ &=14.456\cdot {{T}^{0.3671}} \\ \end{align}\,\! }[/math]
The equation for the instantaneous MTBF growth curve is:
- [math]\displaystyle{ \begin{align} {{\hat{m}}_{i}}&=\frac{1}{1-\alpha }{{{\hat{m}}}_{c}},:\ \ \alpha \not{=}1 \\ &=\frac{1}{1-0.3671}(14.456){{T}^{0.3671}} \\ \end{align}\,\! }[/math]
Example 2
For the data given in columns 1 and 2 of the following table, estimate the Duane parameters using least squares.
| (1)Failure Number | (2)Failure Time(hours) | (3)[math]\displaystyle{ \ln{T_i}\,\! }[/math] | (4)[math]\displaystyle{ \ln{T_i}^2\,\! }[/math] | (5)[math]\displaystyle{ m_c\,\! }[/math] | (6)[math]\displaystyle{ \ln{m_c}\,\! }[/math] | (7)[math]\displaystyle{ \ln{m_c}\cdot\ln{T_i}\,\! }[/math] |
|---|---|---|---|---|---|---|
| 1 | 9.2 | 2.219 | 4.925 | 9.200 | 2.219 | 4.925 |
| 2 | 25 | 3.219 | 10.361 | 12.500 | 2.526 | 8.130 |
| 3 | 61.5 | 4.119 | 16.966 | 20.500 | 3.020 | 12.441 |
| 4 | 260 | 5.561 | 30.921 | 65.000 | 4.174 | 23.212 |
| 5 | 300 | 5.704 | 32.533 | 60.000 | 4.094 | 23.353 |
| 6 | 710 | 6.565 | 43.103 | 118.333 | 4.774 | 31.339 |
| 7 | 916 | 6.820 | 46.513 | 130.857 | 4.874 | 33.241 |
| 8 | 1010 | 6.918 | 47.855 | 126.250 | 4.838 | 33.470 |
| 9 | 1220 | 7.107 | 50.504 | 135.556 | 4.909 | 34.889 |
| 10 | 2530 | 7.836 | 61.402 | 253.000 | 5.533 | 43.359 |
| 11 | 3350 | 8.117 | 65.881 | 304.545 | 5.719 | 46.418 |
| 12 | 4200 | 8.343 | 69.603 | 350.000 | 5.858 | 48.872 |
| 13 | 4410 | 8.392 | 70.419 | 339.231 | 5.827 | 48.895 |
| 14 | 4990 | 8.515 | 72.508 | 356.429 | 5.876 | 50.036 |
| 15 | 5570 | 8.625 | 74.393 | 371.333 | 5.917 | 51.036 |
| 16 | 8310 | 9.025 | 81.455 | 519.375 | 6.253 | 56.431 |
| 17 | 8530 | 9.051 | 81.927 | 501.765 | 6.218 | 56.282 |
| 18 | 9200 | 9.127 | 83.301 | 511.111 | 6.237 | 56.921 |
| 19 | 10500 | 9.259 | 85.731 | 552.632 | 6.315 | 58.469 |
| 20 | 12100 | 9.401 | 88.378 | 605.000 | 6.405 | 60.215 |
| 21 | 13400 | 9.503 | 90.307 | 638.095 | 6.458 | 61.375 |
| 22 | 14600 | 9.589 | 91.945 | 663.636 | 6.498 | 62.305 |
| 23 | 22000 | 9.999 | 99.976 | 956.522 | 6.863 | 68.625 |
| Sum = | 173.013 | 1400.908 | 7600.870 | 121.406 | 974.242 |
Solution
To estimate the parameters using least squares, the values in columns 3, 4, 5, 6 and 7 are calculated. The cumulative MTBF, [math]\displaystyle{ {{m}_{c}}\,\! }[/math], is calculated by dividing the failure time by the failure number. The value of [math]\displaystyle{ \hat{\alpha }\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} \hat{\alpha }&=\frac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}})\ln ({{m}_{ci}})-\tfrac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}})\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{m}_{ci}})}{n}}{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{\left[ \ln ({{T}_{i}}) \right]}^{2}}-\tfrac{{{\left( \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}}) \right)}^{2}}}{n}} \\ & = \frac{974.242-\tfrac{173.013\cdot 121.406}{23}}{1400.908-\tfrac{{{(173.013)}^{2}}}{23}} \\ & = 0.6133 \end{align}\,\! }[/math]
The estimator of [math]\displaystyle{ b\,\! }[/math] is estimated to be:
- [math]\displaystyle{ \begin{align} \hat{b}&={{e}^{\tfrac{1}{n}\left[ \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{m}_{ci}})-\alpha \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}}) \right]}} \\ & = {{e}^{\tfrac{1}{23}(121.406-0.6133\cdot 173.013)}} \\ & = 1.9453 \end{align}\,\! }[/math]
Therefore, the cumulative MTBF becomes:
- [math]\displaystyle{ \begin{align} \hat{m_{c}}&= bT^{\alpha } \\ & =1.9453\cdot {{T}^{0.613}} \\ \end{align}\,\! }[/math]
Using the equation for the instantaneous MTBF growth curve,
- [math]\displaystyle{ \begin{align} {{\hat{m}}_{i}}&=\frac{1}{1-\alpha }{{{\hat{m}}}_{c}},:\ \ \alpha \not{=}1 \\ & =\frac{1}{1-0.613}(1.945){{T}^{0.613}} \\ \end{align}\,\! }[/math]
Example 3
For the data given in the following table, estimate the Duane parameters using least squares.
| Run Number | Failed Unit | Test Time 1 | Test Time 2 | Cumulative Time |
|---|---|---|---|---|
| 1 | 1 | 0.2 | 2.0 | 2.2 |
| 2 | 2 | 1.7 | 2.9 | 4.6 |
| 3 | 2 | 4.5 | 5.2 | 9.7 |
| 4 | 2 | 5.8 | 9.1 | 14.9 |
| 5 | 2 | 17.3 | 9.2 | 26.5 |
| 6 | 2 | 29.3 | 24.1 | 53.4 |
| 7 | 1 | 36.5 | 61.1 | 97.6 |
| 8 | 2 | 46.3 | 69.6 | 115.9 |
| 9 | 1 | 63.6 | 78.1 | 141.7 |
| 10 | 2 | 64.4 | 85.4 | 149.8 |
| 11 | 1 | 74.3 | 93.6 | 167.9 |
| 12 | 1 | 106.6 | 103 | 209.6 |
| 13 | 2 | 195.2 | 117 | 312.2 |
| 14 | 2 | 235.1 | 134.3 | 369.4 |
| 15 | 1 | 248.7 | 150.2 | 398.9 |
| 16 | 2 | 256.8 | 164.6 | 421.4 |
| 17 | 2 | 261.1 | 174.3 | 435.4 |
| 18 | 2 | 299.4 | 193.2 | 492.6 |
| 19 | 1 | 305.3 | 234.2 | 539.5 |
| 20 | 1 | 326.9 | 257.3 | 584.2 |
| 21 | 1 | 339.2 | 290.2 | 629.4 |
| 22 | 1 | 366.1 | 293.1 | 659.2 |
| 23 | 2 | 466.4 | 316.4 | 782.8 |
| 24 | 1 | 504 | 373.2 | 877.2 |
| 25 | 1 | 510 | 375.1 | 885.1 |
| 26 | 2 | 543.2 | 386.1 | 929.3 |
| 27 | 2 | 635.4 | 453.3 | 1088.7 |
| 28 | 1 | 641.2 | 485.8 | 1127 |
| 29 | 2 | 755.8 | 573.6 | 1329.4 |
Solution
The solution to this example follows the same procedure as the previous example. Therefore, from the table shown above:
- [math]\displaystyle{ \begin{align} \underset{i=1}{\overset{29}{\mathop \sum }}\,\ln ({{T}_{i}})= & 154.151 \\ \underset{i=1}{\overset{29}{\mathop \sum }}\,\ln {{({{T}_{i}})}^{2}}= & 902.592 \\ \underset{i=1}{\overset{29}{\mathop \sum }}\,\ln ({{m}_{c}})= & 82.884 \\ \underset{i=1}{\overset{29}{\mathop \sum }}\,\ln ({{T}_{i}})\cdot \ln ({{m}_{c}})= & 483.154 \end{align}\,\! }[/math]
For least squares, the value of [math]\displaystyle{ \alpha \,\! }[/math] is:
- [math]\displaystyle{ \begin{align} \hat{\alpha }&=\frac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}})\ln ({{m}_{ci}})-\tfrac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}})\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{m}_{ci}})}{n}}{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{\left[ \ln ({{T}_{i}}) \right]}^{2}}-\tfrac{{{\left( \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}}) \right)}^{2}}}{n}} \\ & = \frac{483.154-\tfrac{154.151\cdot 82.884}{29}}{902.592-\tfrac{{{(154.151)}^{2}}}{29}} \\ & = 0.5115 \end{align}\,\! }[/math]
The value of the estimator [math]\displaystyle{ b\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} \hat{b}&={{e}^{\tfrac{1}{n}\left[ \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{m}_{ci}})-\alpha \underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln ({{T}_{i}}) \right]}} \\ & = {{e}^{\tfrac{1}{29}(82.884-0.5115\cdot 154.151)}} \\ & = 1.1495 \end{align}\,\! }[/math]
Therefore, the cumulative MTBF is:
- [math]\displaystyle{ \begin{align} \hat{m_{c}}&=bT^{\alpha } & = 1.1495\cdot {{T}^{0.5115}} \end{align}\,\! }[/math]
Using the equation for the instantaneous MTBF growth,
- [math]\displaystyle{ \begin{align} {{\hat{m}}_{i}}&=\frac{1}{1-\alpha }{{{\hat{m}}}_{c}},:\ \ \alpha \not{=}1 \\ & =\frac{1}{1-0.5115}(1.1495){{T}^{0.5115}} \end{align}\,\! }[/math]
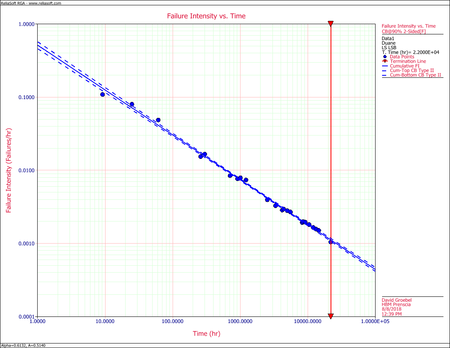
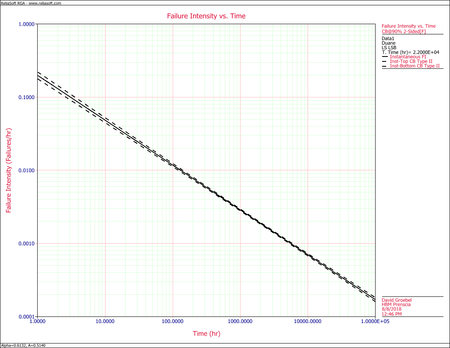
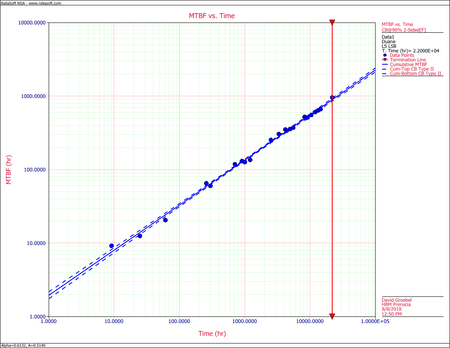
Confidence Bounds Example
Using the values of [math]\displaystyle{ \hat{b}\,\! }[/math] and [math]\displaystyle{ \hat{\alpha }\,\! }[/math] estimated from the least squares analysis in Least Squares Example 2:
- [math]\displaystyle{ \hat{b}=1.9453\,\! }[/math]
- [math]\displaystyle{ \hat{\alpha}=0.6133\,\! }[/math]
Calculate the 90% confidence bounds for the following:
- The parameters [math]\displaystyle{ \alpha\,\! }[/math] and [math]\displaystyle{ b\,\! }[/math].
- The cumulative and instantaneous failure intensity.
- The cumulative and instantaneous MTBF.
Solution
- Use the values of [math]\displaystyle{ \hat{b}\,\! }[/math] and [math]\displaystyle{ \hat{\alpha }\,\! }[/math] estimated from the least squares analysis. Then:
- [math]\displaystyle{ \begin{align} {{S}_{xx}}&=\left[ \underset{i=1}{\overset{n}{\mathop \sum }}\,{{(\ln {{t}_{i}})}^{2}} \right]-\frac{1}{n}{{\left( \underset{i=1}{\overset{n}{\mathop \sum }}\,\ln ({{t}_{i}}) \right)}^{2}} \\ & = 1400.9084-1301.4545 \\ & = 99.4539 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} SE(\hat{\alpha })= & \frac{\sigma }{\sqrt{{{S}_{xx}}}} \\ = & \frac{0.08428}{9.9727} \\ = & 0.008452 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} SE(\ln \hat{b})= & \sigma \cdot \sqrt{\frac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{(\ln {{T}_{i}})}^{2}}}{n\cdot {{S}_{xx}}}} \\ = & 0.065960 \end{align}\,\! }[/math]
- [math]\displaystyle{ C{{B}_{\alpha }}=\hat{\alpha }\pm {{t}_{n-2,\alpha /2}}SE(\hat{\alpha })\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{\alpha }_{L}}= & 0.602050 \\ {{\alpha }_{U}}= & 0.624417 \end{align}\,\! }[/math]
- [math]\displaystyle{ C{{B}_{b}}=\hat{b}{{e}^{\pm {{t}_{n-2,\alpha /2}}SE\left[ \ln (\hat{b}) \right]}}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{b}_{L}}= & 1.7831 \\ {{b}_{U}}= & 2.1231 \end{align}\,\! }[/math]
- The cumulative failure intensity is:
- [math]\displaystyle{ \begin{align} {{\lambda }_{c}}= & \frac{1}{1.9453}\cdot {{22000}^{-0.6133}} \\ = & 0.00111689 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{\lambda }_{i}}= & \frac{1}{1.9453}\cdot (1-0.6133)\cdot {{22000}^{-0.6133}} \\ = & 0.00043198 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{[{{\lambda }_{c}}(t)]}_{L}}= & 0.00106780 \\ {{[{{\lambda }_{c}}(t)]}_{U}}= & 0.00116825 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{[{{\lambda }_{i}}(t)]}_{L}}= & 0.00041299 \\ {{[{{\lambda }_{c}}(t)]}_{U}}= & 0.00045184 \end{align}\,\! }[/math]
- The cumulative MTBF is:
- [math]\displaystyle{ \begin{align} {{m}_{c}}(T)= & 1.9453\cdot {{22000}^{0.6133}} \\ = & 895.3395 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{m}_{i}}(T)= & \frac{1.9453}{1-0.6133}\cdot {{22000}^{0.6133}} \\ = & 2314.9369 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{m}_{c}}{{(t)}_{l}}= & 855.9815 \\ {{m}_{c}}{{(t)}_{u}}= & 936.5071 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{m}_{i}}{{(t)}_{l}}= & 2213.1753 \\ {{m}_{i}}{{(t)}_{u}}= & 2421.3776 \end{align}\,\! }[/math]
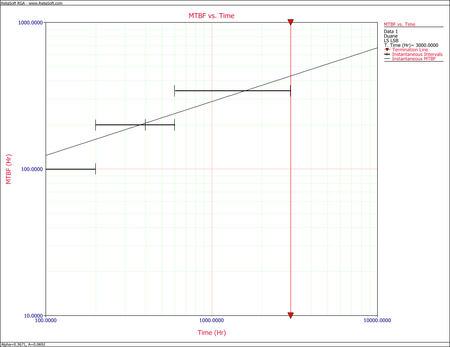
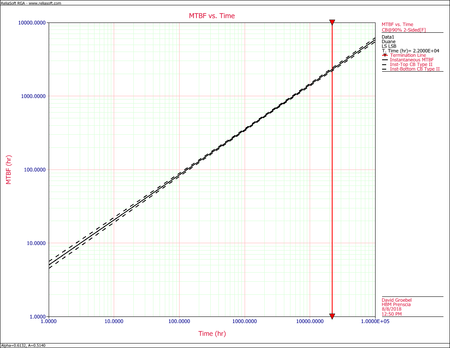
The next figure displays the instantaneous MTBF. Both are plotted with confidence bounds.
Failure Times Data Example
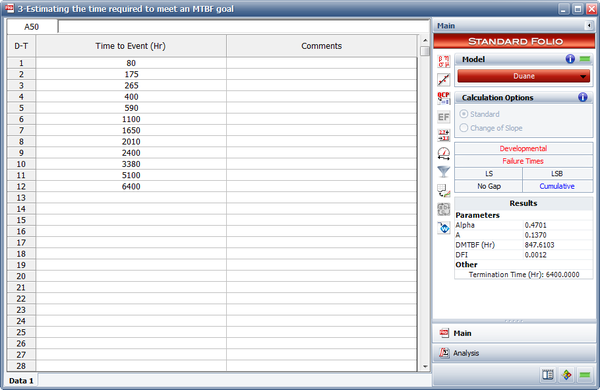
A prototype of a system was tested with design changes incorporated during the test. A total of 12 failures occurred. The data set is given in the following table.
| Failure Number | Cumulative Test Time(hours) |
|---|---|
| 1 | 80 |
| 2 | 175 |
| 3 | 265 |
| 4 | 400 |
| 5 | 590 |
| 6 | 1100 |
| 7 | 1650 |
| 8 | 2010 |
| 9 | 2400 |
| 10 | 3380 |
| 11 | 5100 |
| 12 | 6400 |
Do the following:
- Estimate the Duane parameters.
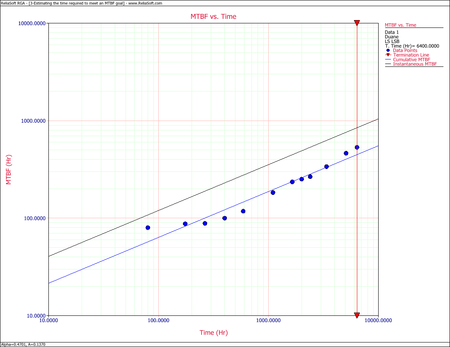
- Plot the cumulative and instantaneous MTBF curves.
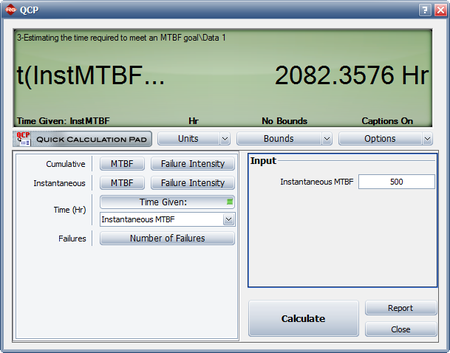
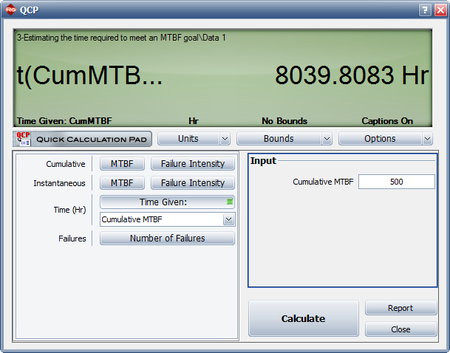
- How many cumulative test and development hours are required to meet an instantaneous MTBF goal of 500 hours?
- How many cumulative test and development hours are required to meet a cumulative MTBF goal of 500 hours?
Solution
- The next figure shows the data entered into RGA along with the estimated Duane parameters.
- The following figure shows the cumulative and instantaneous MTBF curves.
- The next figure shows the cumulative test and development hours needed for an instantaneous MTBF goal of 500 hours.
- The figure below shows the cumulative test and development hours needed for a cumulative MTBF goal of 500 hours.
Discrete Sequential Data Example
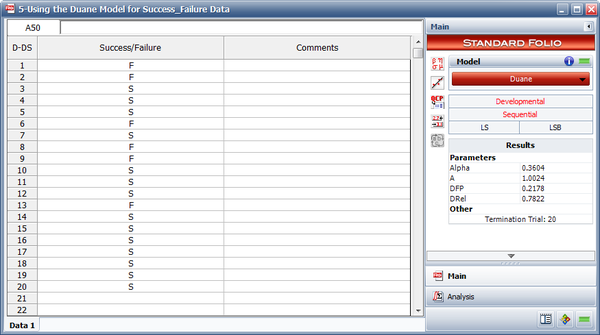
Given the sequential success/failure data in the table below, do the following:
- Estimate the Duane parameters.
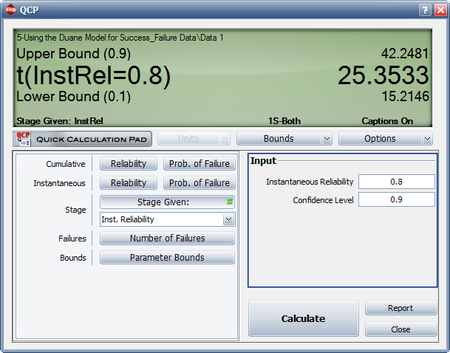
- What is the instantaneous Reliability at the end of the test?
- How many additional test runs with a one-sided 90% confidence level are required to meet an instantaneous Reliability goal of 80%?
| Run Number | Result |
|---|---|
| 1 | F |
| 2 | F |
| 3 | S |
| 4 | S |
| 5 | S |
| 6 | F |
| 7 | S |
| 8 | F |
| 9 | F |
| 10 | S |
| 11 | S |
| 12 | S |
| 13 | F |
| 14 | S |
| 15 | S |
| 16 | S |
| 17 | S |
| 18 | S |
| 19 | S |
| 20 | S |
Solution
- The following figure shows the data set entered into RGA along with the estimated Duane parameters.
- The Reliability at the end of the test is equal to 78.22%. Note that this is the DRel that is shown in the control panel in the above figure.
- The figure below shows the number of test runs with both one-sided confidence bounds at 90% confidence level to achieve an instantaneous Reliability of 80%. Therefore, the number of additional test runs required with a 90% confidence level is equal to [math]\displaystyle{ 42.2481-20=22.2481\approx 23\,\! }[/math] test runs.