Crow Extended - Continuous Evaluation
The Crow Extended model is designed for a single test phase. However, in most cases, testing for a system will be conducted in multiple phases. The Crow Extended - Continuous Evaluation model is designed for analyzing data across multiple test phases, while considering the data for all phases as one data set. To perform the analysis in the RGA software, you would use the Multi-Phase data sheet.
The Crow Extended - Continuous Evaluation (3-parameter) model is an extension of the Crow Extended model, and is designed for practical testing situations where we need the flexibility to apply corrective actions at the time of failure or at a later time during the test, at the end of the current test or during a subsequent test phase. This three-parameter model is free of the constraint where the test must be stopped and all BD modes must be corrected at the end of the test, as in the Crow Extended model. The failure modes can be corrected during the test or when the testing is stopped for the incorporation of the fixes, or even not corrected at all at the end of the test phase. Based on this flexibility, the end time of the test is also not predefined, and it can be continuously updated with new test data. This is the reason behind the name, "continuous evaluation."
Definitions
Classifications
Under the Crow Extended - Continuous Evaluation model, corrective actions can be fixed at the time of failure or delayed to a later time (before time [math]\displaystyle{ T\,\! }[/math], at time [math]\displaystyle{ T\,\! }[/math] or after time [math]\displaystyle{ T\,\! }[/math], where [math]\displaystyle{ T\,\! }[/math] indicates the test's end time). The definition of delayed is expanded to include all type B failure modes corrected after the time of failure. This will include most, if not all, design-related failure modes requiring a root cause failure analysis. Failure modes that are corrected at the time of failure are typically related to human factors, such as manufacturing, operator error, etc.
For the Crow Extended - Continuous Evaluation model, the classifications are defined as follows:
- A indicates that a corrective action will not be performed (management chooses not to address these modes for technical, financial or other reasons).
- BC is defined as a failure mode that receives a corrective action at the time of failure and before the testing resumes. Typically, a type BC failure mode does not require extensive root cause failure analysis, and therefore can be corrected quickly. Type BC modes are generally easy to fix, and are usually related to issues such as quality, manufacturing, operator, etc.
- BD is defined as a failure mode that receives a corrective action at a test time after the first occurrence of the failure mode. Therefore, a fix is considered delayed if it is not implemented at the time of failure. A delayed fix can then occur at a later time during the test, at the end of the test (before the next phase) or during another test phase. Type BD failure modes typically require failure analysis and time to fabricate the corrective action. During the period [math]\displaystyle{ (0,T)\,\! }[/math] into the test, there may be BD modes with corrective actions incorporated into the systems and other BD modes that have been seen, but not yet fixed.
The following table shows a comparison between the definitions of the classifications in the Crow Extended and Crow Extended - Continuous Evaluation models:
| Classification | Crow Extended | Crow Extended - Continuous Evaluation |
|---|---|---|
| A | Corrective action will not be performed | Same as Crow Extended |
| BC | Corrective action during the test | Corrective action at the time of failure |
| BD | Corrective action delayed until after the completion of the test | Corrective action delayed to a test time after the first occurrence of the failure mode |
Reliability growth is achieved by decreasing the failure intensity. The failure intensity for the A failure modes will not change. Therefore, reliability growth can be achieved only by decreasing the BC and BD mode failure intensities. In general, the only part of the BD mode failure intensity that can be decreased is the part that has been seen during testing. The BC failure modes and fixed BD modes (delayed fixes implemented during the test) are corrected during testing, and their failure intensities will not change any more at the end of test.
Event Codes
A Multi-Phase data sheet that is analyzed with the Crow Extended - Continuous Evaluation model has an Event column that allows you to indicate the types of events that occurred during testing. The possible event codes that can be used in the analysis are:
- F: indicates a failure time.
- I: denotes that a fix has been implemented for a BD failure mode at the specific time. BD modes that have not received a corrective action by time [math]\displaystyle{ T\,\! }[/math] would not have an associated I event in the data set.
- Q: indicates that the failure was due to a quality issue. An example of this might be a failure caused by a bolt not being tightened down properly. You have the option to decide whether or not to include quality issues in the analysis. This option can be specified by checking or clearing the Include Q Events check box under Continuous Options on the Analysis tab.
- P: indicates that the failure was due to a performance issue. You can determine whether or not to include performance issues in the analysis. This option can be specified by checking or clearing the Include P Events check box under Continuous Options on the Analysis tab.
- AP: indicates an analysis point. Analysis points can be shown in a multi-phase plot to track overall project progress and can be compared to an idealized growth curve.
- PH: indicates the end of a test phase. Test phases can be shown in a multi-phase plot to track overall project progress and can be compared to planned growth phases. The RGA software allows for a maximum of seven test phases to be defined.
- X: indicates that the data point will be excluded from the analysis. An X can be placed in front of any existing event code or entered by itself. The row of data with the the X will not be included in the analysis.
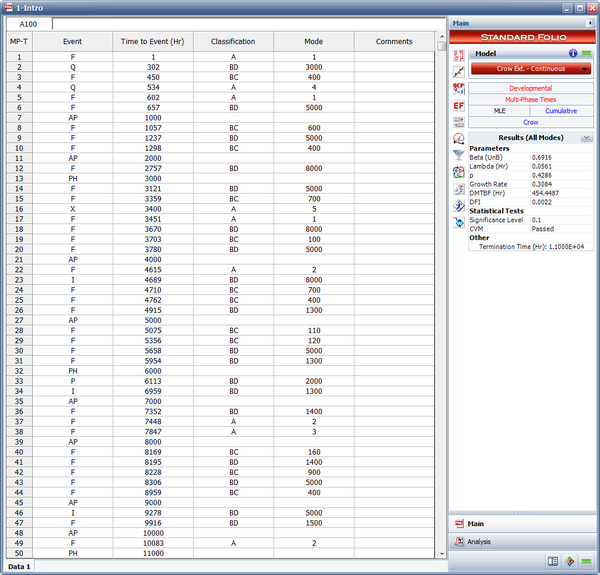
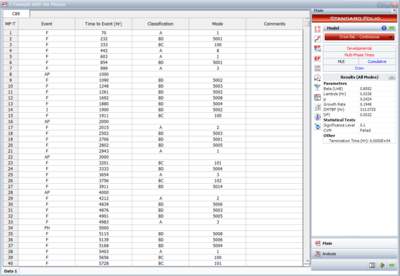
The next figure shows an example of a Crow Extended - Continuous Evaluation folio with all of the possible event codes. As you can see, each failure is indicated with A, BC or BD in the Classification column. In addition, any text can be used to specify the mode. In this figure, failure codes were used in the Mode column for simplicity, but you could just as easily use Seal Leak, or whatever designation you deem appropriate for the failure mode.
[math]\displaystyle{ p\,\! }[/math] Ratio
In the Crow Extended - Continuous evaluation, there is a certain probability of not incorporating a corrective action by time [math]\displaystyle{ T\,\! }[/math]. This is the additional (third parameter), as compared to the Crow Extended model. We define [math]\displaystyle{ p\,\! }[/math] as:
- [math]\displaystyle{ p=\frac{\text{All modes such that, if seen, will be corrected at time }T\text{, or later}}{\text{All failure modes such that, if seen, the corrective action will be delayed}}\,\! }[/math]
It is assumed that the ratio [math]\displaystyle{ p\,\! }[/math] remains fixed over [math]\displaystyle{ (0,T)\,\! }[/math]. This implies that each time a distinct failure mode is seen, the probability that the corrective action is delayed until time [math]\displaystyle{ T\,\! }[/math] or later is [math]\displaystyle{ p\,\! }[/math]. In other words, each time a new BD mode is seen over [math]\displaystyle{ (0,T)\,\! }[/math] there is a probability [math]\displaystyle{ p\,\! }[/math] that the corrective action for that mode will not have been incorporated into the system by time [math]\displaystyle{ T\,\! }[/math]. Under the Crow Extended two-parameter model, this probability is always equal to 1 at time [math]\displaystyle{ T.\,\! }[/math]
Effectiveness Factors
It is very important to note that failure modes are rarely totally eliminated by a corrective action. After failure modes have been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will also remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective the corrective action will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made, and it must be a value between 0 and 1. A study on EFs showed that an average EF, [math]\displaystyle{ d,\,\! }[/math] is about 0.7. Therefore, about [math]\displaystyle{ 30%\,\! }[/math], (i.e., [math]\displaystyle{ 100(1-d)%\,\! }[/math]) of the BD mode failure intensity will typically remain in the system after all of the corrective actions have been implemented. However, individual EFs for the failure modes may be larger or smaller than the average.
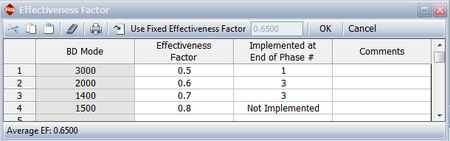
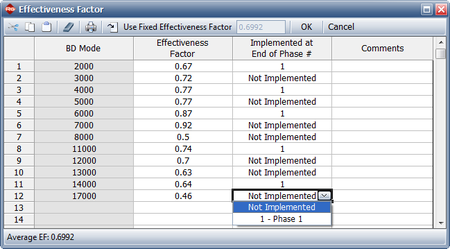
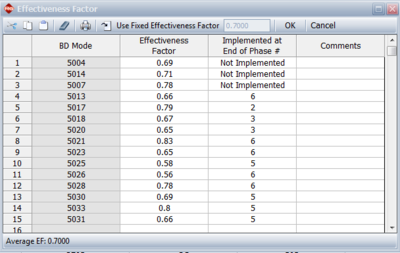
Similar to the Crow Extended model, each BD mode has an effectiveness factor that represents the decrease in failure intensity for that mode once the corrective action has been incorporated into the system. In addition, a delayed fix can be incorporated any time after the first occurrence of the failure mode. Therefore, delayed fixes can be incorporated before the end of the test phase, at the end of the test phase (just like the Crow Extended delayed fixes) or not incorporated at all at the end of the current test phase but postponed for a subsequent test phase. For calculation purposes, any delayed fixes that are incorporated during the test (those with an I event code) do not need to have an effectiveness factor specified, since the fix is already incorporated in the system. The next figure shows how effectiveness factors are defined in the Crow Extended - Continuous Evaluation model in the RGA software. The figure also shows that you can specify whether the delayed fix was actually implemented at the end of the current test phase, at a later phase or not implemented at all.
For a Type BD failure mode that is not yet corrected but still deferred, the Actual Effectiveness Factor for that mode is zero. The Actual Effectiveness Factor for a deferred Type BD failure mode will stay at zero until the point when the corrective action will be incorporated is reached. At that time, the Actual Effectiveness Factor is changed to equal the Assigned Effectiveness Factor for that mode. At this point, the Nominal Effectiveness Factor (the effectiveness factor, assuming that fixes are implemented at the end of the specific phase) and the Actual Effectiveness Factor are the same. In other words, if a fix is not incorporated for a BD mode, its actual effectiveness for reducing failure intensity is zero, and the assigned effectiveness factor will be used only for projecting the MTBF (or failure intensity). This topic will be discussed in the Growth Potential and Projections section.
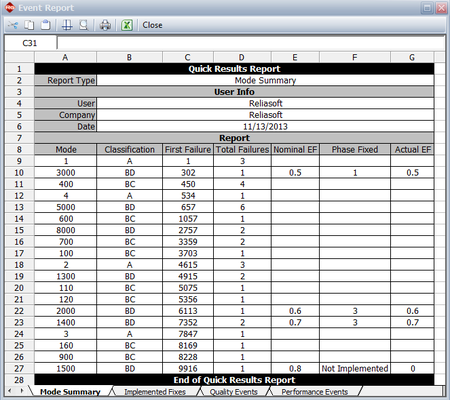
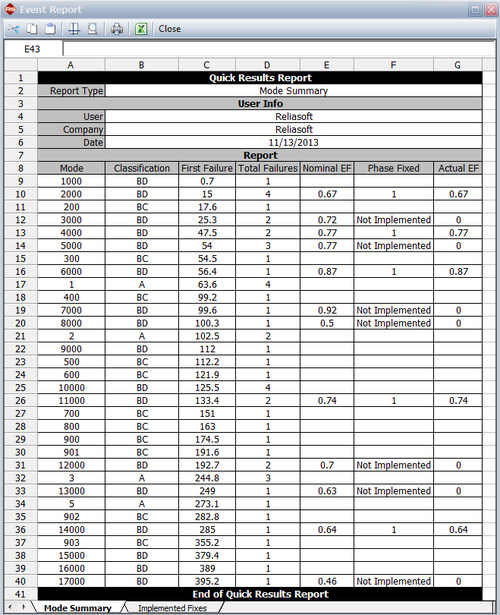
The next figure shows an event report in the RGA software. At the end of the test phase, depending on whether the BD mode was specified as fixed or not fixed, the actual EF is zero (e.g., mode BD3000) or equal to the nominal EF (e.g., mode BD1500).
The Average Nominal EF is:
- [math]\displaystyle{ {{d}_{N}}=\frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M}\,\! }[/math]
where [math]\displaystyle{ M\,\! }[/math] is the total number of open and distinct BD modes at time [math]\displaystyle{ {{T}_{J}}\,\! }[/math], and [math]\displaystyle{ {{d}_{{{N}_{i}}}}\,\! }[/math] is the Nominal Effectiveness Factor as specified for each of the BD mode.
The Average Actual EF is:
- [math]\displaystyle{ {{d}_{A}}=\frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M}\,\! }[/math]
where [math]\displaystyle{ M\,\! }[/math] is the total number of open and distinct BD modes at time [math]\displaystyle{ {{T}_{J}}\,\! }[/math], and [math]\displaystyle{ {{d}_{{{A}_{i}}}}\,\! }[/math] is the Actual Effectiveness Factor at time [math]\displaystyle{ {{T}_{j}}\,\! }[/math] for each BD mode.
Growth Potential and Projections
The failure intensity that remains in the system will depend on the management strategy that determines the classification of the A, BC and BD failure modes. The engineering effort applied to the corrective actions determines the effectiveness factors. In addition, the failure intensity depends on [math]\displaystyle{ h(t)\,\! }[/math], which is the rate at which unique BD failure modes are being discovered during testing. The rate of discovery drives the opportunity to take corrective actions based on the seen failure modes and it is an important factor in the overall reliability growth rate. The reliability growth potential is the limiting value of the failure intensity as time [math]\displaystyle{ T\,\! }[/math] increases. This limit is the maximum MTBF that can be attained with the current management strategy. The maximum MTBF will be attained when all BD modes have been observed and fixed.
If all seen BD modes are corrected by time [math]\displaystyle{ T\,\! }[/math], that is, no deferred corrective actions at time [math]\displaystyle{ T\,\! }[/math], then the growth potential is the maximum attainable based on the type BD designation of the failure modes, the corresponding assigned effectiveness factors and the remaining A modes in the system. This is called the nominal growth potential.
If some seen BD modes are not corrected at the end of the current test phase, then the prevailing growth potential is below the maximum attainable with the type BD designation of the failure modes and the corresponding assigned effectiveness factors.
The Crow-AMSAA (NHPP) model is used to estimate the current demonstrated MTBF or [math]\displaystyle{ MTB{{F}_{D}}.\,\! }[/math] The demonstrated MTBF does not take into account any type of projected improvements. Refer to the Crow-AMSAA (NHPP) chapter for more details.
The corresponding current demonstrated failure intensity is:
- [math]\displaystyle{ \begin{align} {{\lambda }_{D}}=\lambda \beta {{T}^{\beta -1}} \end{align}\,\! }[/math]
or:
- [math]\displaystyle{ {{\lambda }_{D}}=\frac{1}{MTB{{F}_{D}}}\,\! }[/math]
The nominal growth potential factor is:
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ni}} \right)\frac{{{N}_{i}}}{T}\,\! }[/math]
where:
- [math]\displaystyle{ M\,\! }[/math] is the total number of distinct unfixed BD modes at time [math]\displaystyle{ {{T}_{j}}\,\! }[/math].
- [math]\displaystyle{ {{d}_{Ni}}\,\! }[/math] is the assigned (nominal) EF for the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}}.\,\! }[/math]
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the total number of failures over (0, [math]\displaystyle{ {{T}_{j}}\,\! }[/math] ) for the distinct unfixed BD mode [math]\displaystyle{ i\,\! }[/math].
The nominal growth potential factor signifies the failure intensity of the [math]\displaystyle{ M\,\! }[/math] modes after corrective actions have been implemented for them, using the nominal values for the effectiveness factors.
Similarly, the actual growth potential factor is:
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ai}} \right)\frac{{{N}_{i}}}{T}\,\! }[/math]
where [math]\displaystyle{ {{d}_{Ai}}\,\! }[/math] is the actual EF for the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}}.\,\! }[/math]
The actual growth potential factor signifies the failure intensity of the [math]\displaystyle{ M\,\! }[/math] modes after corrective actions have been implemented for them, using the actual values for the effectiveness factors.
Based on the definition of BD modes for the Crow Extended - Continuous Evaluation model, the estimate of [math]\displaystyle{ p\,\! }[/math] at time [math]\displaystyle{ {{T}_{j}}\,\! }[/math] is calculated as follows:
- [math]\displaystyle{ p=\frac{\text{Total number of distinct unfixed BD modes at time }{{T}_{j}}}{\text{Total number of distinct BD modes at time }{{T}_{j}}\text{ (both fixed and unfixed)}}\,\! }[/math]
The unfixed BD mode failure intensity at time [math]\displaystyle{ {{T}_{j}}\,\! }[/math] is:
- [math]\displaystyle{ \lambda_{BDunfixed} = \frac{\text{Total number of unfixed BD failures at time} T_j}{T_j}\,\! }[/math]
Similar to the Crow Extended model, the discovery function at time [math]\displaystyle{ T\,\! }[/math] for the Crow Extended - Continuous Evaluation model is calculated using all the first occurrences of the all the BD modes, both fixed and unfixed. [math]\displaystyle{ h(t)\,\! }[/math] is the unseen BD mode failure intensity and is also the rate at which new unique BD modes are being discovered.
- [math]\displaystyle{ \begin{align} \widehat{h}(T|BD)&= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & \frac{M{{\widehat{\beta }}_{BD}}}{T} \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}\,\! }[/math] is the unbiased estimated of [math]\displaystyle{ \beta \,\! }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of [math]\displaystyle{ M\,\! }[/math] distinct BD modes.
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}\,\! }[/math] is the unbiased estimated of [math]\displaystyle{ \lambda \,\! }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of [math]\displaystyle{ M\,\! }[/math] distinct BD modes.
The parameters [math]\displaystyle{ {{\widehat{\beta }}_{BD}}\,\! }[/math] and [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}\,\! }[/math] are also known as the Rate of Discovery Parameters.
The nominal growth potential failure intensity is:
- [math]\displaystyle{ \lambda_{NGP} = \lambda_D - \lambda_{BD\text{unfixed}} + \lambda_{NGP\text{Factor}} + d_N\cdot p\cdot h(T) - d_N h(T) \,\! }[/math]
and the nominal growth potential MTBF is:
- [math]\displaystyle{ MTB{{F}_{NGP}}=\frac{1}{{{\lambda }_{NGP}}}\,\! }[/math]
The nominal projected failure intensity at time [math]\displaystyle{ T\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} {{\lambda }_{NP}}={{\lambda }_{NGP}}+{{d}_{N}}h(T) \end{align}\,\! }[/math]
and the nominal projected MTBF at time [math]\displaystyle{ T\,\! }[/math] is:
- [math]\displaystyle{ MTB{{F}_{NP}}=\frac{1}{{{\lambda }_{NP}}}\,\! }[/math]
The actual growth potential failure intensity is:
- [math]\displaystyle{ \lambda{AGP} = \lambda_D - \lambda_{BD\text{unfixed}} + \lambda{AGP\text{Factor} + d_A\cdot p\cdot h(T) - d_A h(T)} \,\! }[/math]
and the actual growth potential MTBF is:
- [math]\displaystyle{ MTB{{F}_{AGP}}=\frac{1}{{{\lambda }_{AGP}}}\,\! }[/math]
The actual projected failure intensity at time [math]\displaystyle{ T\,\! }[/math] is:
- [math]\displaystyle{ {{\lambda }_{AP}}={{\lambda }_{AGP}}+{{d}_{A}}\cdot h\left( T \right)\,\! }[/math]
and the actual projected MTBF at time [math]\displaystyle{ T\,\! }[/math] is:
- [math]\displaystyle{ MTB{{F}_{AP}}=\frac{1}{{{\lambda }_{AP}}}\,\! }[/math]
In terms of confidence intervals and goodness-of-fit tests, the calculations are the same as for the Crow Extended model.
Example - Single Phase
The following table shows a date set with failure and fix implementation events.
| Multi-Phase Data for a Time Terminated Test at [math]\displaystyle{ T=400\,\! }[/math] | ||||||||
| Event | Time to Event | Classification | Mode | Event | Time to Event | Classification | Mode | |
|---|---|---|---|---|---|---|---|---|
| F | 0.7 | BD | 1000 | F | 244.8 | A | 3 | |
| F | 15 | BD | 2000 | F | 249 | BD | 13000 | |
| F | 17.6 | BC | 200 | F | 250.8 | A | 2 | |
| F | 25.3 | BD | 3000 | F | 260.1 | BD | 2000 | |
| F | 47.5 | BD | 4000 | F | 273.1 | A | 5 | |
| I | 50 | BD | 1000 | F | 274.7 | BD | 11000 | |
| F | 54 | BD | 5000 | I | 280 | BD | 9000 | |
| F | 54.5 | BC | 300 | F | 282.8 | BC | 902 | |
| F | 56.4 | BD | 6000 | F | 285 | BD | 14000 | |
| F | 63.6 | A | 1 | F | 315.4 | BD | 4000 | |
| F | 72.2 | BD | 5000 | F | 317.1 | A | 3 | |
| F | 99.2 | BC | 400 | F | 320.6 | A | 1 | |
| F | 99.6 | BD | 7000 | F | 324.5 | BD | 12000 | |
| F | 100.3 | BD | 8000 | F | 324.9 | BD | 10000 | |
| F | 102.5 | A | 2 | F | 342 | BD | 5000 | |
| F | 112 | BD | 9000 | F | 350.2 | BD | 3000 | |
| F | 112.2 | BC | 500 | F | 355.2 | BC | 903 | |
| F | 120.9 | BD | 2000 | F | 364.6 | BD | 10000 | |
| F | 121.9 | BC | 600 | F | 364.9 | A | 1 | |
| F | 125.5 | BD | 10000 | I | 365 | BD | 10000 | |
| F | 133.4 | BD | 11000 | F | 366.3 | BD | 2000 | |
| F | 151 | BC | 700 | F | 379.4 | BD | 15000 | |
| F | 163 | BC | 800 | F | 389 | BD | 16000 | |
| F | 174.5 | BC | 900 | I | 390 | BD | 15000 | |
| F | 177.4 | BD | 10000 | I | 393 | BD | 16000 | |
| F | 191.6 | BC | 901 | F | 394.9 | A | 3 | |
| F | 192.7 | BD | 12000 | F | 395.2 | BD | 17000 | |
| F | 213 | A | 1 | |||||
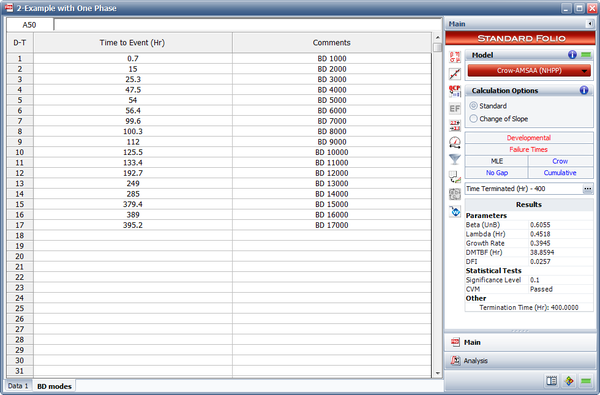
The following figure shows the data set entered in the RGA software's Multi-Phase data sheet. Note that because this is a time terminated test with a single phase ending at [math]\displaystyle{ T=400\,\! }[/math], the last event entry is a phase (PH) with time to event = 400.
The next figure shows the effectiveness factors for the unfixed BD modes, and information concerning whether the fix will be implemented. Since we have only one test phase for this example, the notation "1" indicates that the fix will be implemented at the end of the first (and only) phase.
Do the following:
- Determine the current demonstrated MTBF and failure intensity at time [math]\displaystyle{ T\,\! }[/math].
- Determine the nominal and actual average effectiveness factor at time [math]\displaystyle{ T\,\! }[/math].
- Determine the [math]\displaystyle{ p\,\! }[/math] ratio.
- Determine the nominal and actual growth potential factor.
- Determine the unfixed BD mode failure intensity at time [math]\displaystyle{ T.\,\! }[/math]
- Determine the rate of discovery parameters and the rate of discovery function at time [math]\displaystyle{ T.\,\! }[/math]
- Determine the nominal growth potential failure intensity and MTBF at time [math]\displaystyle{ T.\,\! }[/math]
- Determine the nominal projected failure intensity and MTBF at time [math]\displaystyle{ T.\,\! }[/math]
- Determine the actual growth potential failure intensity and MTBF at time [math]\displaystyle{ T.\,\! }[/math]
- Determine the actual projected failure intensity and MTBF at time [math]\displaystyle{ T.\,\! }[/math]
Solution
- As described in the Crow-AMSAA (NHPP) chapter, for a time terminated test, [math]\displaystyle{ \beta \,\! }[/math] is estimated by the following equation:
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \widehat{\lambda }= & \frac{n}{{{T}^{*\beta }}} \\ = & \frac{50}{{{400}^{0.9866}}} \\ = & 0.1354 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} MTB{{F}_{D}}= & \frac{1}{\lambda \beta {{T}^{\beta -1}}} \\ = & 8.1087 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{\lambda }_{D}}= & \frac{1}{MTB{{F}_{D}}} \\ = & 0.1233 \end{align}\,\! }[/math]
- The average nominal effectiveness factor at time [math]\displaystyle{ T\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ = & \frac{0.67+0.72+0.77+0.77+0.87+0.92+0.5+0.74+0.7+0.63+0.64+0.46}{12} \\ = & 0.6992 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{d}_{A}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M} \\ = & \frac{0.67+0+0.77+0+0.87+0+0+0.74+0+0+0.64+0}{12} \\ = & 0.3075 \end{align}\,\! }[/math]
- The [math]\displaystyle{ p\,\! }[/math] ratio is calculated by:
- [math]\displaystyle{ \begin{align} p= & \frac{\text{Total number of distinct unfixed BD modes at time }400}{\text{Total number of distinct BD modes at time }400\text{ (both fixed and unfixed)}} \\ = & \frac{12}{12+5} \\ = & 0.7059 \end{align}\,\! }[/math]
- The nominal growth potential factor is:
- [math]\displaystyle{ {{\lambda }_{NGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ni}} \right)\frac{{{N}_{i}}}{T}\,\! }[/math]
- [math]\displaystyle{ {{d}_{Ni}}\,\! }[/math] is the assigned (nominal) EF for the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}},\,\! }[/math] (which is shown in the picture of the Effectiveness Factors window given above).
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the total number of failures over (0, 400) for the distinct unfixed BD mode [math]\displaystyle{ i\,\! }[/math]. This is summarized in the following table.
Number of Failures for Unfixed BD Modes Classification Mode Number of Failures BD 2000 4 BD 3000 2 BD 4000 2 BD 5000 3 BD 6000 1 BD 7000 1 BD 8000 1 BD 11000 2 BD 12000 2 BD 13000 1 BD 14000 1 BD 17000 1 Sum = 21 Based on the information given above, the nominal growth potential factor is calculated as:
- [math]\displaystyle{ \begin{align} {{\lambda }_{NGPFactor}}=0.0153 \end{align}\,\! }[/math]
The actual growth potential factor is:
- [math]\displaystyle{ {{\lambda }_{AGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ai}} \right)\frac{{{N}_{i}}}{T}\,\! }[/math]
where [math]\displaystyle{ {{d}_{Ai}}\,\! }[/math] is the actual EF for the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] unfixed BD mode at time 400, depending on whether a fix was implemented at time 400 or not. The next figure shows an event report from the RGA software where the actual EF is zero if a fix was not implemented at 400, or equal to the nominal EF if the fix was implemented at 400.
Based on the information given above, the actual growth potential factor is calculated as:
- [math]\displaystyle{ \begin{align} {{\lambda }_{AGPFactor}}=0.0344 \end{align}\,\! }[/math]
- The total number of unfixed BD modes listed in the data table is 21. The unfixed BD mode failure intensity at time 400 is:
- [math]\displaystyle{ \begin{align} {{\lambda}_{BD unfixed}}= & \frac{\text{Total number of unfixed BD failure at time 400}}{400}\\ = & \frac{21}{400}\\ = & 0.0525 \end{align}\,\! }[/math]
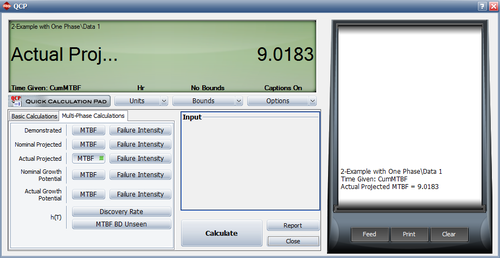
- The discovery rate parameters at time 400 are calculated by using all the first occurrences of all the BD modes, both fixed and unfixed. [math]\displaystyle{ {{\hat{\beta }}_{BD}}\,\! }[/math] is the unbiased estimated of [math]\displaystyle{ \beta \,\! }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes in our example. [math]\displaystyle{ {{\hat{\lambda }}_{BD}}\,\! }[/math] is the unbiased estimate of [math]\displaystyle{ \lambda \,\! }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes. The next figure shows the first time to failure for each of the 17 distinct modes and the results of the analysis using the Crow-AMSAA (NHPP) model in the RGA software (note that in this case, the calculation settings in the User Setup is configured to calculate the unbiased [math]\displaystyle{ \beta \,\! }[/math]).
So we have:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6055\,\! }[/math]
and:
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.4518\,\! }[/math]
The equations used to determine these parameters have been explained in question 1 of this example and are also presented in detail in the Crow-AMSA (NHPP) chapter.
The discovery rate function at time 400 is:
- [math]\displaystyle{ \begin{align} \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ = & 0.4518\cdot 0.6055\cdot {{400}^{0.6055-1}} \\ = & 0.0257 \end{align}\,\! }[/math]
This is the failure intensity of the unseen BD modes at time 400. In this case, it means that 0.0257 new BD modes are discovered per hour, or one new BD mode is discovered every 38.9 hours.
- The nominal growth potential failure intensity is:
- [math]\displaystyle{ \begin{align} {{\lambda}_{NGP}}= & {{\lambda}_{D}} - {{\lambda }_{BD unfixed}} + {{\lambda }_{NGP Factor}} + {{d}_{N}} \cdot p \cdot h (400) - {{d}_{N}}h (400) \\ = & 0.1233 - 0.0525 + 0.0153 + 0.6992 \cdot 0.7059 \cdot 0.0257 - 0.6992 \cdot 0.0257\\ = & 0.080 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} MTB{{F}_{NGP}}= & \frac{1}{{{\lambda }_{NGP}}} \\ = & \frac{1}{0.080} \\ = & 12.37 \end{align}\,\! }[/math]
- The nominal projected failure intensity at time [math]\displaystyle{ 400\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} {{\lambda }_{NP}}= & {{\lambda }_{NGP}}+{{d}_{N}}h(400) \\ = & 0.080+0.6992\cdot 0.0257 \\ = & 0.0988 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} MTB{{F}_{NP}}= & \frac{1}{{{\lambda }_{NP}}} \\ = & \frac{1}{0.0988} \\ = & 10.11 \end{align}\,\! }[/math]
- The actual growth potential failure intensity is:
- [math]\displaystyle{ \begin{align} {{\lambda}_{AGP}}= & {{\lambda}_{D}} - {{\lambda }_{BD unfixed}} + {{\lambda }_{AGP Factor}} + {{d}_{A}} \cdot p \cdot h (400) - {{d}_{A}}h (400) \\ = & 0.1233 - 0.0525 + 0.0344 + 0.3075 \cdot 0.7059 \cdot 0.0257 - 0.3075 \cdot 0.0257\\ = & 0.1029 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} MTB{{F}_{AGP}}= & \frac{1}{{{\lambda }_{AGP}}} \\ = & \frac{1}{0.1029} \\ = & 9.71 \end{align}\,\! }[/math]
- The actual projected failure intensity at time 400 is:
- [math]\displaystyle{ \begin{align} {{\lambda }_{AP}}= & {{\lambda }_{AGP}}+{{d}_{A}}\cdot h\left( 400 \right) \\ = & 0.1029+0.3075\cdot 0.0257 \\ = & 0.1108 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} MTB{{F}_{AP}}= & \frac{1}{{{\lambda }_{AP}}} \\ = & \frac{1}{0.1108} \\ = & 9.01 \end{align}\,\! }[/math]
Example - Six Phases
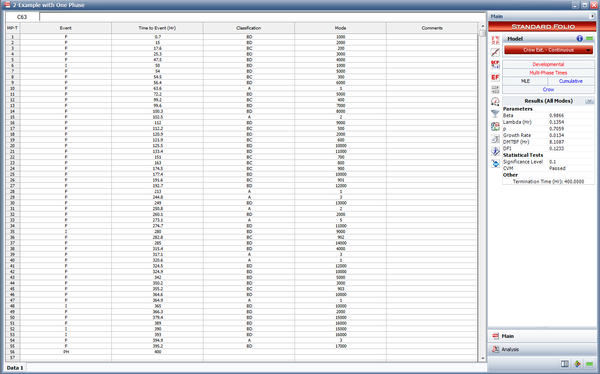
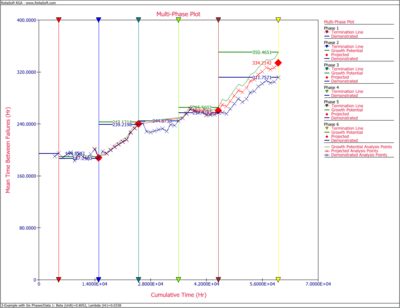
The Crow Extended - Continuous Evaluation model allows data analysis across multiple phases, up to seven individual phases. The next figure shows a portion of failure time test results obtained across six phases. Analysis points are specified for continuous evaluation every 1,000 hours. The cumulative test times at the end of each test phase are 5,000; 15,000; 25,000; 35,000; 45,000 and 60,000 hours.
The next figure shows the effectiveness factors for the BD modes that do not have an associated fix implementation event. In other words, these are unfixed BD modes. Note that this specifies the phase after which the BD mode will be fixed, if any.
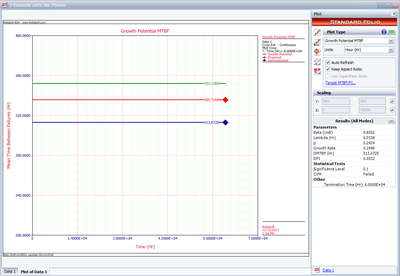
The next plot shows the overall test results in terms of demonstrated, projected and growth potential MTBF.
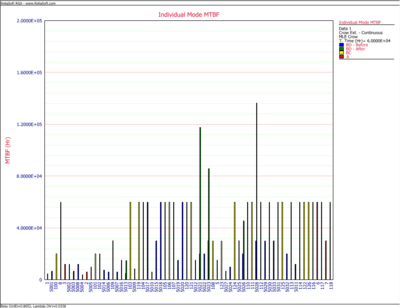
The next chart shows the "before" and "after" MTBFs for all the individual modes. Note that the "after" MTBFs are calculated by taking into account the respective effectiveness factors for each of the unfixed BD modes.
The analysis points are used to track overall growth inside and across phases, at desired intervals. The RGA software allows you to create a multi-phase plot that is associated with a multi-phase data sheet. In addition, if you have an existing growth planning folio in your RGA project, the multi-phase plot can plot the results from the multi-phase data sheet together with the reliability growth model from the growth planning folio. This allows you to track the overall reliability program against the goals, and set plans at each stage of the test. Additional information on combining a growth planning folio and a multi-phase plot is presented in the Reliability Growth Planning chapter.
The next figure shows the multi-phase plot for the six phases of the reliability growth test program. This plot can be a powerful tool for overall tracking of the reliability growth program. It displays the termination time for each phase of testing, along with the demonstrated, projected and growth potential MTBFs at those times. The plot also displays the calculated MTBFs at specified analysis points, which are determined based on the "AP" events in the data sheet.
Mixed Data
The Crow Extended - Continuous Evaluation model also can be applied for discrete data from one-shot (success/failure) testing. In the RGA software, you can create a multi-phase data sheet that is configured for mixed data to accommodate data from tests where a single unit is tested for each successive configuration (individual trial-by-trial), where multiple units are tested for each successive configuration (configurations in groups) or a combination of both.
Corrective actions cannot take place at the time of failure for discrete data. With that in mind, the mixed data type does not allow for BC modes. The delayed corrective actions over time can be either fixed or unfixed, based on a subsequent implementation (I) event. So, for discrete data there are only unfixed BD modes or fixed BD modes. As a practical application, think of a multi-phase program for missile systems. Because the systems are one-shot items, the fixes for the failure modes are delayed until at least the next trial.
Note that for calculation purposes, it is required to have at least three failures in the first interval. If that is not the case, then the data set needs to be grouped until this requirement is met before calculating. The RGA software performs this operation in the background.
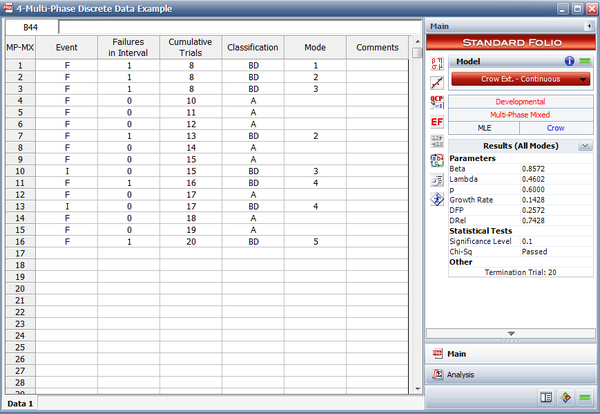
Example - Multi-Phase Discrete Data
A one-shot system underwent reliability growth development for a total of 20 trials. The test was performed as a combination of configuration in groups and individual trial-by-trial. The following table shows the obtained data set. The Failures in Interval column specifies the number of failures that occurred in each interval, and the Cumulative Trials column specifies the cumulative number of trials at the end of that interval.
| Mixed Data | ||||
| Event | Failures in Interval | Cumulative Trials | Classification | Mode |
|---|---|---|---|---|
| F | 1 | 8 | BD | 1 |
| F | 1 | 8 | BD | 2 |
| F | 1 | 8 | BD | 3 |
| F | 0 | 10 | A | |
| F | 0 | 11 | A | |
| F | 0 | 12 | A | |
| F | 1 | 13 | BD | 2 |
| F | 0 | 14 | A | |
| F | 0 | 15 | A | |
| I | 0 | 15 | BD | 3 |
| F | 1 | 16 | BD | 4 |
| F | 0 | 17 | A | |
| I | 0 | 17 | BD | 4 |
| F | 0 | 18 | A | |
| F | 0 | 18 | A | |
| F | 1 | 20 | BD | 5 |
The table also gives the classifications of the failure modes. There are 5 BD modes. Of these 5 modes, 2 are corrected during the test (BD3 and BD4) and 3 have not been corrected by time [math]\displaystyle{ T=20\,\! }[/math] (BD1, BD2 and BD5). Do the following:
- Calculate the parameters of the Crow Extended - Continuous Evaluation model.
- Calculated the demonstrated reliability at the end of the test.
- Calculate parameter [math]\displaystyle{ p\,\! }[/math].
- Calculate the unfixed BD mode failure probability.
- Calculate the nominal growth potential factor.
- Calculate the nominal average effectiveness factor.
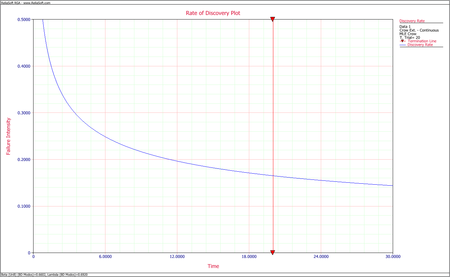
- Calculate the discovery failure intensity function at the end of the test.
- Calculate the nominal projected reliability at the end of the test.
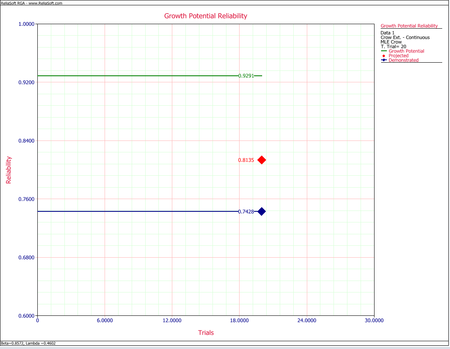
- Calculate the nominal growth potential reliability at the end of the test.
Solution
- The next figure shows the data entered in the RGA software.
The parameters [math]\displaystyle{ \beta \,\! }[/math] and [math]\displaystyle{ \lambda \,\! }[/math] are calculated as follows (the calculations for these parameters are presented in detail in the Crow-AMSAA (NHPP) chapter):
- [math]\displaystyle{ \widehat{\beta }=0.8572\,\! }[/math]
and:
- [math]\displaystyle{ \widehat{\lambda }=0.4602\,\! }[/math]
- The corresponding demonstrated unreliability is calculated as:
- [math]\displaystyle{ \begin{align} {{f}_{D}}=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 \end{align}\,\! }[/math]
- [math]\displaystyle{ {{f}_{D}}(20)=0.8572\cdot 0.4602\cdot {{20}^{0.8572-1}}=0.2572\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{R}_{D}}= & 1-{{f}_{D}} \\ = & 1-0.2572=0.7428 \end{align}\,\! }[/math]
- Assume that the following effectiveness factors are assigned to the unfixed BD modes:
Classification Mode Effectiveness Factor Implemented at End of Phase BD 1 0.65 Phase 1 BD 2 0.70 Phase 1 BD 5 0.75 Phase 1 The parameter [math]\displaystyle{ p\,\! }[/math] is the total number of distinct unfixed BD modes at time [math]\displaystyle{ T\,\! }[/math] divided by the total number of distinct BD (fixed and unfixed) modes.
In this example:
- [math]\displaystyle{ p=\frac{3}{5}=0.6\,\! }[/math]
- The unfixed BD mode failure probability at time [math]\displaystyle{ T\,\! }[/math] is the total number of unfixed BD failures (classified at time [math]\displaystyle{ T\,\! }[/math] ) divided by the total trials. Based on the table at the beginning of the example, we have:
- [math]\displaystyle{ {{f}_{BD, unfixed}}=\frac{4}{20}=0.2\,\! }[/math]
- The nominal growth potential factor is:
- [math]\displaystyle{ \begin{align} {{\lambda }_{NGPFactor}}= & \underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{i}} \right)\frac{{{N}_{i}}}{T} \\ = & \left( 1-{{d}_{1}} \right)\frac{{{N}_{1}}}{T}+\left( 1-{{d}_{2}} \right)\frac{{{N}_{2}}}{T}+\left( 1-{{d}_{5}} \right)\frac{{{N}_{5}}}{T} \\ = & \left( 1-0.65 \right)\frac{1}{20}+\left( 1-0.70 \right)\frac{2}{20}+\left( 1-0.75 \right)\frac{1}{20} \\ = & 0.06 \end{align}\,\! }[/math]
- The nominal average effectiveness factor is:
- [math]\displaystyle{ \begin{align} {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ = & \frac{0.65+0.70+0.75}{3} \\ = & 0.70 \end{align}\,\! }[/math]
- The discovery function at time [math]\displaystyle{ T\,\! }[/math] is calculated using all the first occurrences of all the BD modes, both fixed and unfixed. In our example, we calculate [math]\displaystyle{ {{\widehat{\beta }}_{BD}}\,\! }[/math] and [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}\,\! }[/math] using only the unfixed BD modes and excluding the second occurrence of BD2, which results in the following:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6602\,\! }[/math]
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.6920\,\! }[/math]
- [math]\displaystyle{ \begin{align} \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ = & 0.6920\cdot 0.6602\cdot {{20}^{0.6602-1}} \\ = & 0.16507 \end{align}\,\! }[/math]
- The nominal projected failure probability at time [math]\displaystyle{ T=20\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} {{f}_{NP}}= & {{f}_{NGP}}+{{d}_{N}}h(T) \\ = & 0.0701+0.7\cdot 0.16507 \\ = & 0.1865 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{R}_{P}}= & 1-0.1856= \\ = & 0.8135 \end{align}\,\! }[/math]
- The nominal growth potential unreliability is:
- [math]\displaystyle{ {{f}_{NGP}} = {{f}_{D}} - {{f}_{BD unfixed}} + {{\lambda}_{NGPFactor}} + {{d}_{N}}\cdot p \cdot h(T) - {{d}_{N}}h(T)\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{f}_{NGP}}= & 0.2572-0.2+0.06+0.7\cdot 0.6\cdot 0.16507-0.7\cdot 0.16507 \\ = & 0.0709 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{R}_{NGP}}= & 1-0.0709 \\ = & 0.9291 \end{align}\,\! }[/math]
Statistical Tests for Effectiveness of Corrective Actions
The purpose of the statistical tests is to explore the effectiveness of corrective actions during or at the end of a phase. Say we have two phases, phase 1 and phase 2. Suppose that corrective actions are incorporated during or at the end of phase 1. The system is then operated during phase 2. The general question is whether or not the corrective actions have been effective.
There are two questions that can be addressed regarding the effectiveness of the corrective actions:
Question 1. Is the average failure intensity for phase 2 statistically less than the average failure intensity for phase1?
Question 2. Is the average failure intensity for phase 2 statistically less than the Crow-AMSAA (NHPP) instantaneous failure intensity at the end of phase 1?
Average Failure Intensities Test
The purpose of this test is to compare the average failure intensity during phase 2 with the average failure intensity during phase 1.
The average failure intensity for phase 1 is:
- [math]\displaystyle{ {{\overline{r}}_{1}}=\frac{{{N}_{1}}}{{{T}_{1}}}\,\! }[/math]
where [math]\displaystyle{ {{T}_{1}}\,\! }[/math] is the phase 1 test time and [math]\displaystyle{ {{N}_{1}}\,\! }[/math] is the number of failures during phase 1.
Similarly, the average failure intensity for phase 2 is:
- [math]\displaystyle{ {{\overline{r}}_{2}}=\frac{{{N}_{2}}}{{{T}_{2}}}\,\! }[/math]
where [math]\displaystyle{ {{T}_{2}}\,\! }[/math] is the phase 2 test time and [math]\displaystyle{ {{N}_{2}}\,\! }[/math] is the number of failures during phase 2.
The overall test time, [math]\displaystyle{ T\,\! }[/math], is:
- [math]\displaystyle{ \begin{align} T={{T}_{1}}+{{T}_{2}} \end{align}\,\! }[/math]
The overall number of failures, [math]\displaystyle{ N\,\! }[/math], is:
- [math]\displaystyle{ \begin{align} N={{N}_{1}}+{{N}_{2}} \end{align}\,\! }[/math]
Define [math]\displaystyle{ P\,\! }[/math] as:
- [math]\displaystyle{ P=\frac{{{T}_{2}}}{T}\,\! }[/math]
If the cumulative binomial probability [math]\displaystyle{ B(k;P,N)\,\! }[/math] of up to [math]\displaystyle{ {{N}_{2}}\,\! }[/math] failures is less than or equal to the statistical significance [math]\displaystyle{ \alpha \,\! }[/math], then the average failure intensity for phase 2 is statistically less than the average failure intensity for phase 1 at the specific significance level.
The cumulative binomial distribution probability is given by:
- [math]\displaystyle{ B(k;P,N)=\underset{f=0}{\overset{k}{\mathop \sum }}\,\left( \begin{matrix} N \\ f \\ \end{matrix} \right){{P}^{f}}{{\left( 1-P \right)}^{N-f}}\,\! }[/math]
which gives the probability that the test failures, [math]\displaystyle{ f\,\! }[/math], are less than or equal to the number of allowable failures, or acceptance number [math]\displaystyle{ k\,\! }[/math] in [math]\displaystyle{ N\,\! }[/math] trials, when each trial has a probability of succeeding of [math]\displaystyle{ P\,\! }[/math].
Example
Suppose a test is being conducted and is divided into two phases. The test time for the first phase is [math]\displaystyle{ {{T}_{1}}=27\,\! }[/math] days, and the test time for the second phase is [math]\displaystyle{ {{T}_{2}}=18\,\! }[/math] days. The number of failures during phase 1 is [math]\displaystyle{ {{N}_{1}}=11\,\! }[/math], and the number of failures during phase 2 is [math]\displaystyle{ {{N}_{2}}=2.\,\! }[/math]
The average failure intensity for phase 1 is:
- [math]\displaystyle{ {{\overline{r}}_{1}}=\frac{{{N}_{1}}}{{{T}_{1}}}=\frac{11}{27}=0.4074.\,\! }[/math]
Similarly, the average failure intensity for phase 2 is:
- [math]\displaystyle{ {{\overline{r}}_{2}}=\frac{{{N}_{2}}}{T2}=\frac{2}{18}=0.1111\,\! }[/math]
Although the average failure intensities are different, we want to see, if at the 10% statistical significance level, the average failure intensity for phase 2 is statistically less than the average failure intensity for phase 1.
Solution
Concerning the total test time, we have:
- [math]\displaystyle{ \begin{align} T={{T}_{1}}+{{T}_{2}}=27+18=45 \end{align}\,\! }[/math]
The total number of failures is equal to:
- [math]\displaystyle{ \begin{align} N={{N}_{1}}+{{N}_{2}}=11+2=13 \end{align}\,\! }[/math]
Then, we calculate [math]\displaystyle{ P\,\! }[/math] as:
- [math]\displaystyle{ P=\frac{{{T}_{2}}}{T}=\frac{18}{45}=0.4\,\! }[/math]
Using the cumulative binomial distribution probability equation, we have:
- [math]\displaystyle{ \begin{align} B(k;P,N)= & B({{N}_{2}};P,N) \\ = & \underset{f=0}{\overset{{{N}_{2}}}{\mathop \sum }}\,\left( \begin{matrix} N \\ {{N}_{2}} \\ \end{matrix} \right){{P}^{f}}{{\left( 1-P \right)}^{N-f}} \\ = & \underset{f=0}{\overset{2}{\mathop \sum }}\,\left( \begin{matrix} 13 \\ f \\ \end{matrix} \right){{0.4}^{f}}{{\left( 1-0.4 \right)}^{13-f}} \\ = & 0.058 \end{align}\,\! }[/math]
Because 0.058 is lower than 0.10, the conclusion is that at the 10% significance level of the the average failure intensity for phase 2 is statistically less than the average failure intensity for phase 1. The conclusion would be different for a different significance level. For example, at the 5% significance level, since 0.058 is not lower than 0.05, we fail to reject the null hypothesis. In other words, we cannot statistically prove any significant difference between the average failure intensities at the 5% level.
Average vs. Demonstrated Failure Intensities Test
The purpose of this test is to compare the average failure intensity during phase 2 with the Crow-AMSAA (NHPP) instantaneous (demonstrated) failure intensity at the end of phase 1.
Once again, the average failure intensity for phase 2 is given by:
- [math]\displaystyle{ \overline{r_{2}}=\frac{N_{2}}{T_{2}} }[/math]
where [math]\displaystyle{ T_{2}\,\! }[/math] is the phase 2 test time and [math]\displaystyle{ N_{2}\,\! }[/math] is the number of failures during phase 2.
The Crow-AMSAA (NHPP) model estimate of failure intensity at time is [math]\displaystyle{ \hat{r}(T_{1}) }[/math]. Dr. Larry H. Crow [16] showed that the Crow-AMSAA (NHPP) estimate is approximately distributed as a random variable with standard deviation [math]\displaystyle{ \textstyle \sqrt{\frac{N_{1}}{2}} }[/math].
We therefore treat [math]\displaystyle{ \hat{r}(T_{1}) }[/math] as an approximate Poisson random variable with number of failures:
- [math]\displaystyle{ N_{1}^{*}=\frac{N_{1}}{2} }[/math]
We also set:
- [math]\displaystyle{ T_{1}^{*}=\frac{N_{1}^{*}}{\hat{r}(T_{1})} }[/math]
Then we define:
- [math]\displaystyle{ T=T_{1}^{*} + T_{2} }[/math]
and:
- [math]\displaystyle{ N=N_{1}^{*} + N_{2} }[/math]
Let:
- [math]\displaystyle{ P=\frac{T_{2}}{T} }[/math]
If the cumulative binomial probability [math]\displaystyle{ B(k;P,N)\,\! }[/math] of up to [math]\displaystyle{ N_{2}\,\! }[/math] failures is less than or equal to the statistical significance [math]\displaystyle{ \alpha_{1}\,\! }[/math], then the average failure intensity for phase 2 is statistically less than the Crow-AMSAA (NHPP) instantaneous failure intensity at the end of phase 1, at the specific significance level. The cumulative binomial distribution probability is again given by:
- [math]\displaystyle{ B(k;P,N)=\underset{f=0}{\overset{k}{\mathop \sum }}\,\left( \begin{matrix} N \\ f \\ \end{matrix} \right){{P}^{f}}{{\left( 1-P \right)}^{N-f}}\,\! }[/math]
Example
Suppose a test is being conducted and is divided into two phases. The test time for the first phase is [math]\displaystyle{ T_{1}=21\,\! }[/math] days, and the test time for the second phase is [math]\displaystyle{ T_{2} = 18\,\! }[/math] days. The number of failures during phase 1 is [math]\displaystyle{ N_{1}=11\,\! }[/math] and the number of failures during phase 2 is [math]\displaystyle{ N_{2}=2\,\! }[/math]. The Crow-AMSAA (NHPP) parameters for the first phase are [math]\displaystyle{ \beta = 0.7189\,\! }[/math] and [math]\displaystyle{ \lambda = 1.0288\,\! }[/math].
The demonstrated failure intensity at the end of phase 1 is calculated as follows:
- [math]\displaystyle{ \begin{align} \hat{r}(T_{1}) &= \lambda \beta T^{\beta - 1} \\ &= 1.0288 \cdot 0.7189 \cdot 27^{0.7189-1} \\ &= 0.2929 \end{align} }[/math]
The average failure intensity for phase 2 is:
- [math]\displaystyle{ \overline{r}_{2} = \frac{N_{2}}{T_{2}} = \frac{2}{8} = 0.1111 }[/math]
Determine if the average failure intensity for phase 2 is statistically less than the demonstrated failure intensity at the end of phase 1 at the 10% significance level.
Solution
We calculate the number of failures [math]\displaystyle{ N_{1}^{*} }[/math] as:
- [math]\displaystyle{ N_{1}^{*}=\frac{N_{1}}{2}= \frac{11}{2}=5.5 }[/math]
Then:
- [math]\displaystyle{ T_{1}^{*}= \frac{N_{1}^{*}}{\hat{r}(T_{1})}= \frac{5.5}{0.2929}= 18.78 }[/math]
Concerning the total test time, we have:
- [math]\displaystyle{ T = T_{1}^{*} + T_{2} = 18.78 + 18 = 36.78 }[/math]
Concerning the total number of failures, we have:
- [math]\displaystyle{ N = N_{1}^{*} + N_{2} = 5.5 + 2 = 7.5 }[/math]
Then we calculate [math]\displaystyle{ P }[/math] as:
- [math]\displaystyle{ P = \frac{T_{2}}{T} = \frac{18}{36.78} = 0.4894 }[/math]
Since the number of failures [math]\displaystyle{ N = 7.5\,\! }[/math] is not an integer, we are going to calculate the cumulative binomial probabilities for [math]\displaystyle{ N = 7\,\! }[/math] and [math]\displaystyle{ N = 8\,\! }[/math], and then interpolate to [math]\displaystyle{ N = 7.5\,\! }[/math].
For [math]\displaystyle{ N = 7\,\! }[/math], we have:
- [math]\displaystyle{ \begin{align} B(k;P,N) &= B(N_{2};P,N)\\ &= B(2;0.4894,7) \\ &= \sum_{f=0}^{N_{2}}\begin{pmatrix}N\\ N_{2}\end{pmatrix}p^{f}(1-P)^{N-f} \\ &= \sum_{f=0}^{2}\begin{pmatrix}7\\ f\end{pmatrix}0.4894^{f}(1-0.4849)^{7-f} \\ &= 0.244 \end{align} }[/math]
And for [math]\displaystyle{ N=8\,\! }[/math], we have:
- [math]\displaystyle{ \begin{align} B(k;P,N) &= B(N_{2};P,N)\\ &= B(2;0.4894,8) \\ &= \sum_{f=0}^{N_{2}}\begin{pmatrix}N\\ N_{2}\end{pmatrix}p^{f}(1-P)^{N-f} \\ &= \sum_{f=0}^{2}\begin{pmatrix}8\\ f\end{pmatrix}0.4894^{f}(1-0.4849)^{8-f} \\ &= 0.158 \end{align} }[/math]
A linear interpolation between two data points [math]\displaystyle{ (x_{a},y_{a})\,\! }[/math] and [math]\displaystyle{ (x_{b},y_{b})\,\! }[/math] at the [math]\displaystyle{ (x,y)\,\! }[/math] interpolant is given by:
- [math]\displaystyle{ y = y_{a} + (x - x_{a})\frac{(y_{b}-y_{a})}{(x_{b}-x_{a})}\,\! }[/math]
So for [math]\displaystyle{ N = 7.5\,\! }[/math] we would have that:
- [math]\displaystyle{ \begin{align} B(N_{2};P,7.5) &= B(N_{2};P,7) + (7.5 - 7)\frac{B(N_{2};P,8)-B(N_{2};P,7)}{8-7} \\ &= 0.244 + (7.5 - 7) \frac{0.158 - 0.244}{8 - 7} \\ &= 0.201 \end{align} }[/math]
Since 0.201 is greater than 0.10, the conclusion is that at the 10% significance level the average failure intensity for phase 2 is not statistically different compared to the demonstrated failure intensity at the end of phase 1.
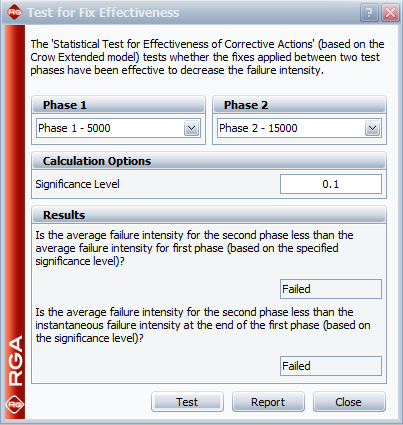
Using the example with the six phases that was given earlier in this chapter, the following figure shows the application of the two statistical tests in RGA.