Grouped per Configuration - Standard Gompertz Model
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability growth reference.
A new design is put through a reliability growth test. The requirement is that after the ninth stage the design will exhibit an 85% reliability with a 90% confidence level. Given the data in the following table, do the following:
- Estimate the parameters of the standard Gompertz model.
- What is the initial reliability at [math]\displaystyle{ T=0\,\! }[/math] ?
- Determine the reliability at the end of the ninth stage and check to see whether the goal has been met.
| Stage | Number of Units | Number of Failures |
|---|---|---|
| 1 | 10 | 5 |
| 2 | 8 | 3 |
| 3 | 9 | 3 |
| 4 | 9 | 2 |
| 5 | 10 | 2 |
| 6 | 10 | 1 |
| 7 | 10 | 1 |
| 8 | 10 | 1 |
| 9 | 10 | 1 |
Solution
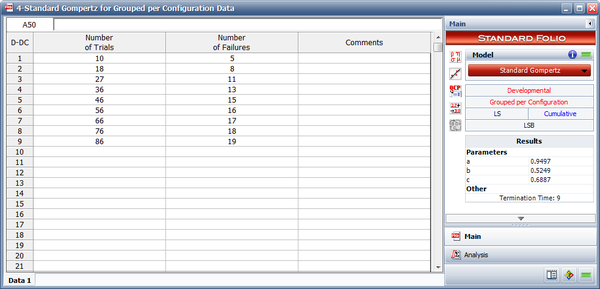
- The data is entered in cumulative format and the estimated standard Gompertz parameters are shown in the following figure.
- The initial reliability at [math]\displaystyle{ T=0\,\! }[/math] is equal to:
- [math]\displaystyle{ \begin{align} {{R}_{T=0}}= & a\cdot b \\ = & 0.9497\cdot 0.5249 \\ = & 0.4985 \end{align}\,\! }[/math]
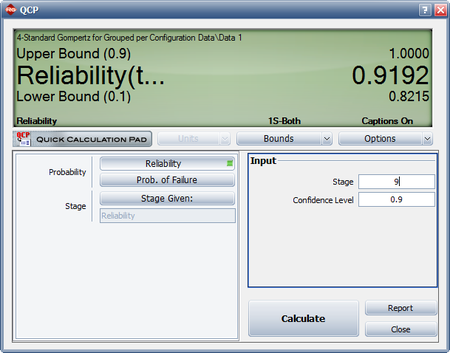
- The reliability at the ninth stage can be calculated using the Quick Calculation Pad (QCP) as shown in the figure below.
The estimated reliability at the end of the ninth stage is equal to 91.92%. However, the lower limit at the 90% 1-sided confidence bound is equal to 82.15%. Therefore, the required goal of 85% reliability at a 90% confidence level has not been met.