Using Pools and Crews
Using Resources: Pools and Crews
In order to make the analysis more realistic, one may wish to consider additional sources of delay times in the analysis or study the effect of limited resources. In the prior examples, we used a repair distribution to identify how long it takes to restore a component. The factors that one chooses to consider in this time may include the time it takes to do the repair and/or the time it takes to get a crew, a spare part, etc. While all of these factors may be included in the repair duration, optimized usage of these resources can only be achieved if the resources are studied individually and their dependencies are identified.
As an example, consider the situation where two components in parallel fail at the same time and only a single repair person is available. Because this person would not be able to execute the repair on both components simultaneously, an additional delay will be encountered that also needs to be included in the modeling. One way to accomplish this is to assign a specific repair crew to each component.
Including Crews
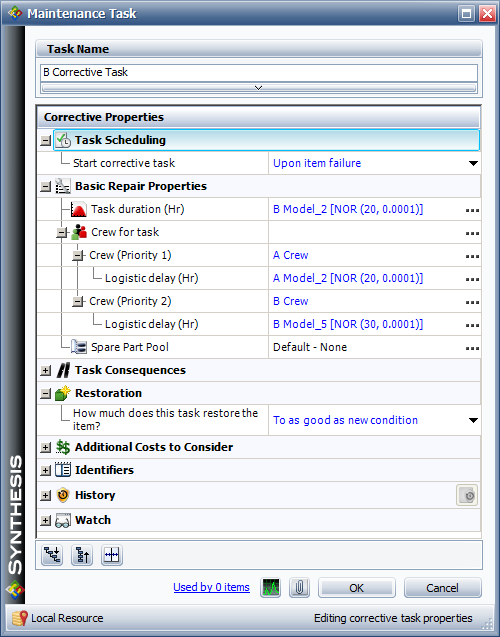
BlockSim allows you to assign maintenance crews to each component and one or more crews may be assigned to each component from the Maintenance Task Properties window. Note that there may be different crews for each action, (i.e., corrective, preventive, on condition and inspection).
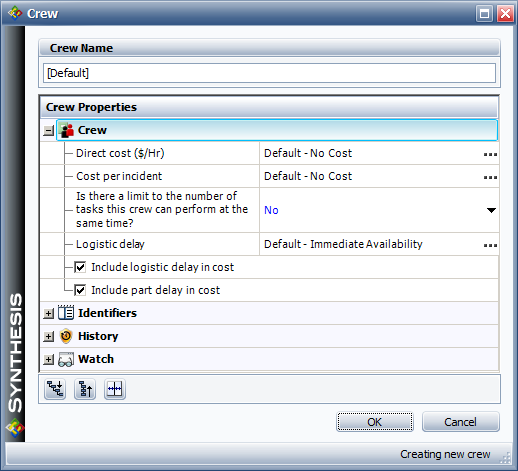
A crew record needs to be defined for each named crew, as shown in the picture below. The basic properties for each crew include factors such as:
- Logistic delays. How long does it take for the crew to arrive?
- Is there a limit to the number of tasks this crew can perform at the same time? If yes, how many simultaneous tasks can the crew perform?
- What is the cost per hour for the crew?
- What is the cost per incident for the crew?
Illustrating Crew Use
To illustrate the use of crews in BlockSim, consider the deterministic scenario described by the following RBD and properties.
| Unit | Failure | Repair | Crew |
|---|---|---|---|
| [math]\displaystyle{ A\,\! }[/math] | [math]\displaystyle{ 100\,\! }[/math] | [math]\displaystyle{ 10\,\! }[/math] | Crew [math]\displaystyle{ A\,\! }[/math] : Delay = 20, Single Task |
| [math]\displaystyle{ B\,\! }[/math] | [math]\displaystyle{ 120\,\! }[/math] | [math]\displaystyle{ 20\,\! }[/math] | Crew [math]\displaystyle{ A\,\! }[/math] : Delay = 20, Single Task |
| [math]\displaystyle{ C\,\! }[/math] | [math]\displaystyle{ 140\,\! }[/math] | [math]\displaystyle{ 20\,\! }[/math] | Crew [math]\displaystyle{ A\,\! }[/math] : Delay = 20, Single Task |
| [math]\displaystyle{ D\,\! }[/math] | [math]\displaystyle{ 160\,\! }[/math] | [math]\displaystyle{ 10\,\! }[/math] | Crew [math]\displaystyle{ A\,\! }[/math] : Delay = 20, Single Task |
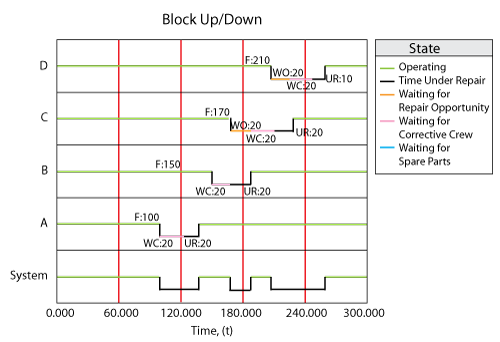
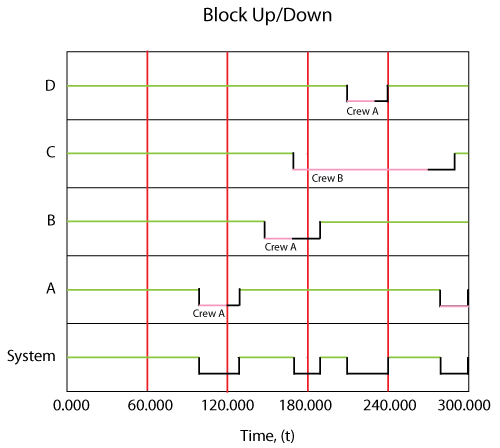
As shown in the figure above, the System Up/Down plot illustrates the sequence of events, which are:
- At 100, [math]\displaystyle{ A\,\! }[/math] fails. It takes 20 to get the crew and 10 to repair, thus the component is repaired by 130. The system is failed/down during this time.
- At 150, [math]\displaystyle{ B\,\! }[/math] fails since it would have accumulated an operating age of 120 by this time. It again has to wait for the crew and is repaired by 190.
- At 170, [math]\displaystyle{ C\,\! }[/math] fails. Upon this failure, [math]\displaystyle{ C\,\! }[/math] requests the only available crew. However, this crew is currently engaged by [math]\displaystyle{ B\,\! }[/math] and, since the crew can only perform one task at a time, it cannot respond immediately to the request by [math]\displaystyle{ C\,\! }[/math]. Thus, [math]\displaystyle{ C\,\! }[/math] will remain failed until the crew becomes available. The crew will finish with unit [math]\displaystyle{ B\,\! }[/math] at 190 and will then be dispatched to [math]\displaystyle{ C\,\! }[/math]. Upon dispatch, the logistic delay will again be considered and [math]\displaystyle{ C\,\! }[/math] will be repaired by 230. The system continues to operate until the failures of [math]\displaystyle{ B\,\! }[/math] and [math]\displaystyle{ C\,\! }[/math] overlap (i.e., the system is down from 170 to 190)
- At 210, [math]\displaystyle{ D\,\! }[/math] fails. It again has to wait for the crew and repair.
- [math]\displaystyle{ D\,\! }[/math] is up at 260.
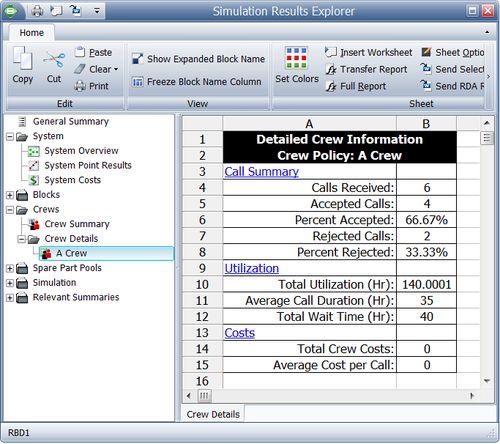
The following figure shows an example of some of the possible crew results (details), which are presented next.
Explanation of the Crew Details
- Each request made to a crew is logged.
- If a request is successful (i.e., the crew is available), the call is logged once in the Calls Received counter and once in the Accepted Calls counter.
- If a request is not accepted (i.e., the crew is busy), the call is logged once in the Calls Received counter and once in the Rejected Calls counter. When the crew is free and can be called upon again, the call is logged once in the Calls Received counter and once in the Accepted Calls counter.
- In this scenario, there were two instances when the crew was not available, Rejected Calls = 2, and there were four instances when the crew performed an action, Calls Accepted = 4, for a total of six calls, Calls Received = 6.
- Percent Accepted and Percent Rejected are the ratios of calls accepted and calls rejected with respect to the total calls received.
- Total Utilization is the total time that the crew was used. It includes both the time required to complete the repair action and the logistic time. In this case, this is 140, or:
- [math]\displaystyle{ \begin{align} {{T}_{{{R}_{A}}}}= & 10,{{T}_{{{L}_{A}}}}=20 \\ {{T}_{{{R}_{B}}}}= & 20,{{T}_{{{L}_{B}}}}=20 \\ {{T}_{{{R}_{C}}}}= & 20,{{T}_{{{L}_{C}}}}=20 \\ {{T}_{{{R}_{D}}}}= & 10,{{T}_{{{L}_{D}}}}=20 \\ {{T}_{U}}= & \left( {{T}_{{{R}_{A}}}}+{{T}_{{{L}_{A}}}} \right)+\left( {{T}_{{{R}_{B}}}}+{{T}_{{{L}_{B}}}} \right) \\ & +\left( {{T}_{{{R}_{C}}}}+{{T}_{{{L}_{C}}}} \right)+\left( {{T}_{{{R}_{D}}}}+{{T}_{{{L}_{D}}}} \right) \\ {{T}_{U}}= & 140 \end{align}\,\! }[/math]
- 6. Average Call Duration is the average duration of each crew usage, and it also includes both logistic and repair time. It is the total usage divided by the number of accepted calls. In this case, this is 35.
- 7. Total Wait Time is the time that blocks in need of a repair waited for this crew. In this case, it is 40 ( [math]\displaystyle{ C\,\! }[/math] and [math]\displaystyle{ D\,\! }[/math] both waited 20 each).
- 8. Total Crew Costs are the total costs for this crew. It includes the per incident charge as well as the per unit time costs. In this case, this is 180. There were four incidents at 10 each for a total of 40, as well as 140 time units of usage at 1 cost unit per time unit.
- 9. Average Cost per Call is the total cost divided by the number of accepted calls. In this case, this is 45.
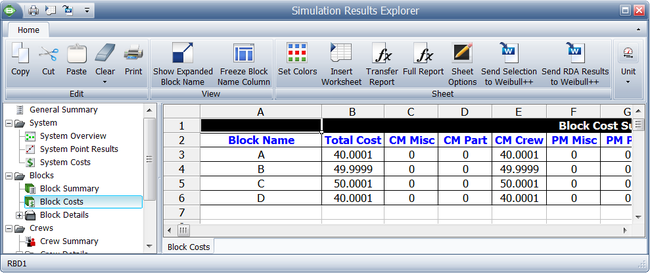
Note that crew costs that are attributed to individual blocks can be obtained from the Blocks reports, as shown in the figure below.
How BlockSim Handles Crews
- Crew logistic time is added to each repair time.
- The logistic time is always present, and the same, regardless of where the crew was called from (i.e., whether the crew was at another job or idle at the time of the request).
- For any given simulation, each crew's logistic time is constant (taken from the distribution) across that single simulation run regardless of the task (CM, PM or inspection).
- A crew can perform either a finite number of simultaneous tasks or an infinite number.
- If the finite limit of tasks is reached, the crew will not respond to any additional request until the number of tasks the crew is performing is less than its finite limit.
- If a crew is not available to respond, the component will "wait" until a crew becomes available.
- BlockSim maintains the queue of rejected calls and will dispatch the crew to the next repair on a "first come, first served" basis.
- Multiple crews can be assigned to a single block (see overview in the next section).
- If no crew has been assigned for a block, it is assumed that no crew restrictions exist and a default crew is used. The default crew can perform an infinite number of simultaneous tasks and has no delays or costs.
Looking at Multiple Crews
Multiple crews may be available to perform maintenance for a particular component. When multiple crews have been assigned to a block in BlockSim, the crews are assigned to perform maintenance based on their order in the crew list, as shown in the figure below.
In the case where more than one crew is assigned to a block, and if the first crew is unavailable, then the next crew is called upon and so forth. As an example, consider the prior case but with the following modifications (i.e., Crews [math]\displaystyle{ A\,\! }[/math] and [math]\displaystyle{ B\,\! }[/math] are assigned to all blocks):
| Unit | Failure | Repair | Crew |
|---|---|---|---|
| [math]\displaystyle{ A\,\! }[/math] | [math]\displaystyle{ 100\,\! }[/math] | [math]\displaystyle{ 10\,\! }[/math] | [math]\displaystyle{ A,B\,\! }[/math] |
| [math]\displaystyle{ B\,\! }[/math] | [math]\displaystyle{ 120\,\! }[/math] | [math]\displaystyle{ 20\,\! }[/math] | [math]\displaystyle{ A,B\,\! }[/math] |
| [math]\displaystyle{ C\,\! }[/math] | [math]\displaystyle{ 140\,\! }[/math] | [math]\displaystyle{ 20\,\! }[/math] | [math]\displaystyle{ A,B\,\! }[/math] |
| [math]\displaystyle{ D\,\! }[/math] | [math]\displaystyle{ 160\,\! }[/math] | [math]\displaystyle{ 10\,\! }[/math] | [math]\displaystyle{ A,B\,\! }[/math] |
| Crew [math]\displaystyle{ A\,\! }[/math] ; Delay = 20, Single Task |
| Crew [math]\displaystyle{ B\,\! }[/math] ; Delay = 30, Single Task |
The system would behave as shown in the figure below.
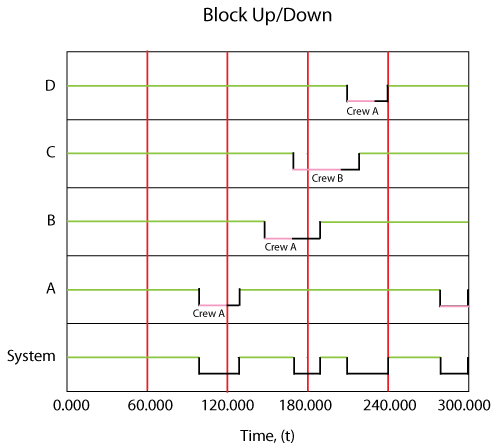
In this case, Crew [math]\displaystyle{ B\,\! }[/math] was used for the [math]\displaystyle{ C\,\! }[/math] repair since Crew [math]\displaystyle{ A\,\! }[/math] was busy. On all others, Crew [math]\displaystyle{ A\,\! }[/math] was used. It is very important to note that once a crew has been assigned to a task it will complete the task. For example, if we were to change the delay time for Crew [math]\displaystyle{ B\,\! }[/math] to 100, the system behavior would be as shown in the figure below.
In other words, even though Crew [math]\displaystyle{ A\,\! }[/math] would have finished the repair on [math]\displaystyle{ C\,\! }[/math] more quickly if it had been available when originally called, [math]\displaystyle{ B\,\! }[/math] was assigned the task because [math]\displaystyle{ A\,\! }[/math] was not available at the instant that the crew was needed.
Additional Rules on Crews
- 1. If all assigned crews are engaged, the next crew that will be chosen is the crew that can get there first.
- a) This accounts for the time it would take a particular crew to complete its current task (or all tasks in its queue) and its logistic time.
- 2. If a crew is available, it gets used regardless of what its logistic delay time is.
- a) In other words, if a crew with a shorter logistic time is busy, but almost done, and another crew with a much higher logistic time is currently free, the free one will get assigned to the task.
- 3. For each simulation each crew's logistic time is computed (taken randomly from its distribution or its fixed time) at the beginning of the simulation and remains constant across that one simulation for all actions (CM, PM and inspection).
- 1. If all assigned crews are engaged, the next crew that will be chosen is the crew that can get there first.
Using Spare Part Pools
BlockSim also allows you to specify spare part pools (or depots). Spare part pools allow you to model and manage spare part inventory and study the effects associated with limited inventories. Each component can have a spare part pool associated with it. If a spare part pool has not been defined for a block, BlockSim's analysis assumes a default pool of infinite spare parts. To speed up the simulation, no details on pool actions are kept during the simulation if the default pool is used.
Pools allow you to define multiple aspects of the spare part process, including stock levels, logistic delays and restock options. Every time a part is repaired under a CM or scheduled action (PM, OC and Inspection), a spare part is obtained from the pool. If a part is available in the pool, it is then used for the repair. Spare part pools perform their actions based on the simulation clock time.
Spare Properties
A spare part pool is identified by a name. The general properties of the pool are its stock level (must be greater than zero), cost properties and logistic delay time. If a part is available (in stock), the pool will dispense that part to the requesting block after the specified logistic time has elapsed. One needs to think of a pool as an independent entity. It accepts requests for parts from blocks and dispenses them to the requesting blocks after a given logistic time. Requests for spares are handled on a first come, first served basis. In other words, if two blocks request a part and only one part is in stock, the first block that made the request will receive the part. Blocks request parts from the pool immediately upon the initiation of a CM or scheduled event (PM, OC and Inspection).
Restocking the Pool
If the pool has a finite number of spares, restock actions may be incorporated. The figure below shows the restock properties. Specifically, a pool can restock itself either through a scheduled restock action or based on specified conditions.
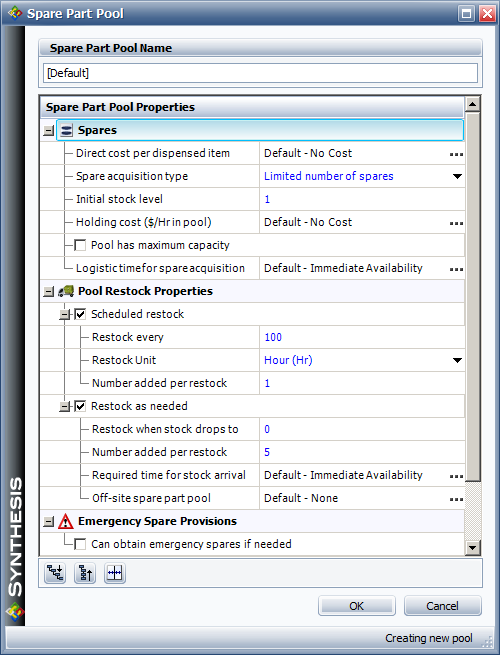
A scheduled restock action adds a set number of parts to the pool on a predefined scheduled part arrival time. For the settings in the figure above, one spare part would be added to the pool every 100 hours, based on the system (simulation) time. In other words, for a simulation of 1,000 hours, a spare part would arrive at 100 hours, 200 hours, etc. The part is available to the pool immediately after the restock action and without any logistic delays.
In an on-condition restock, a restock action is initiated when the stock level reaches (or is below) a specified value. In figure above, five parts are ordered when the stock level reaches 0. Note that unlike the scheduled restock, parts added through on-condition restock become available after a specified logistic delay time. In other words, when doing a scheduled restock, the parts are pre-ordered and arrive when needed. Whereas in the on-condition restock, the parts are ordered when the condition occurs and thus arrive after a specified time. For on-condition restocks, the condition is triggered if and only if the stock level drops to or below the specified stock level, regardless of how the spares arrived to the pool or were distributed by the pool. In addition, the restock trigger value must be less than the initial stock.
Lastly, a maximum capacity can be assigned to the pool. If the maximum capacity is reached, no more restock actions are performed. This maximum capacity must be equal to or greater than the initial stock. When this limit is reached, no more items are added to the pool. For example, if the pool has a maximum capacity of ten and a current stock level of eight and if a restock action is set to add five items to the pool, then only two will be accepted.
Obtaining Emergency Spares
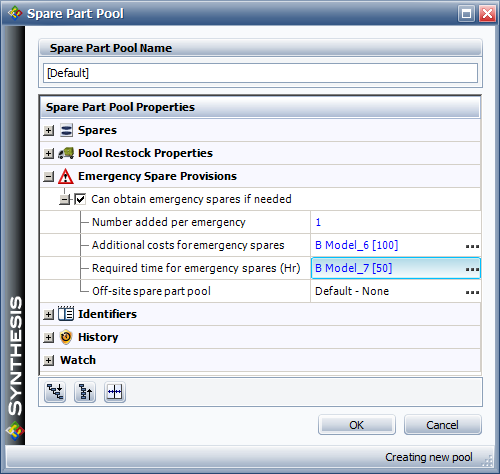
Emergency restock actions can also be defined. The figure below illustrates BlockSim's Emergency Spare Provisions options. An emergency action is triggered only when a block requests a spare and the part is not currently in stock. This is the only trigger condition. It does not account for whether a part has been ordered or if one is scheduled to arrive. Emergency spares are ordered when the condition is triggered and arrive after a time equal to the required time to obtain emergency spare(s).
Summary of Rules for Spare Part Pools
The following rules summarize some of the logic when dealing with spare part pools.
Basic Logic Rules
- 1. Queue Based: Requests for spare parts from blocks are queued and executed on a "first come, first served" basis.
- 2. Emergency: Emergency restock actions are performed only when a part is not available.
- 3. Scheduled Restocks: Scheduled restocks are added instantaneously to the pool at the scheduled time.
- 4. On-Condition Restock: On-condition restock happens when the specified condition is reached (e.g., when the stock drops to two or if a request is received for a part and the stock is below the restock level).
- a) For example, if a pool has three items in stock and it dispenses one, an on-condition restock is initiated the instant that the request is received (without regard to the logistic delay time). The restocked items will be available after the required time for stock arrival has elapsed.
- b) The way that this is defined allows for the possibility of multiple restocks. Specifically, every time a part needs to be dispensed and the stock is lower than the specified quantity, parts are ordered. In the case of a long logistic delay time, it is possible to have multiple re-orders in the queue.
- 5. Parts Become Available after Spare Acquisition Logistic Delay: If there is a spare acquisition logistic time delay, the requesting block will get the part after that delay.
- a) For example, if a block with a repair duration of 10 fails at 100 and requests a part from a pool with a logistic delay time of 10, that block will not be up until 120.
- 6. Compound Delays: If a part is not available and an emergency part (or another part) can be obtained, then the total wait time for the part is the sum of both the logistic time and the required time to obtain a spare.
- 7. First Available Part is Dispensed to the First Block in the Queue: The pool will dispense a requested part if it has one in stock or when it becomes available, regardless of what action (i.e., as needed restock or emergency restock) that request may have initiated.
- a) For example, if Block A requests a part from a pool and that triggers an emergency restock action, but a part arrives before the emergency restock through another action (e.g., scheduled restock), then the pool will dispense the newly arrived part to Block A (if Block A is next in the queue to receive a part).
- 8. Blocks that Trigger an Action Get Charged with the Action: A block that triggers an emergency restock is charged for the additional cost to obtain the emergency part, even if it does not use an emergency part (i.e., even if another part becomes available first).
- 9. Triggered Action Cannot be Canceled. If a block triggers a restock action but then receives a part from another source, the action that the block triggered is not canceled.
- a) For example, if Block A initiates an emergency restock action but was then able to use a part that became available through other actions, the emergency request is not canceled and an emergency spare part will be added to the pool's stock level.
- b) Another way to explain this is by looking at the part acquisition logistic times as transit times. Because an ordered part is en-route to you after you order it, you will receive it regardless of whether the conditions have changed and you no longer need it.
Simultaneous Dispatch of Crews and Parts Logic
Some special rules apply when a block has both logistic delays in acquiring parts from a pool and when waiting for crews. BlockSim dispatches requests for crews and spare parts simultaneously. The repair action does not start until both crew and part arrive, as shown next.
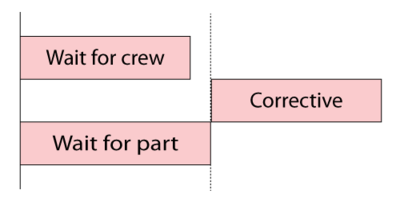
If a crew arrives and it has to wait for a part, then this time (and cost) is added to the crew usage time.
Example Using Both Crews and Pools
Consider the following example, using both crews and pools.
where:

And the crews are:

While the spare pool is:
The behavior of this system from 0 to 300 is shown graphically in the figure below.
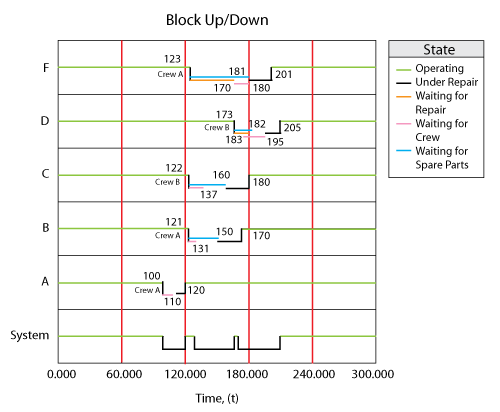
The discrete system events during that time are as follows:
- 1. Component [math]\displaystyle{ A\,\! }[/math] fails at 100 and Crew [math]\displaystyle{ A\,\! }[/math] is engaged.
- a) At 110, Crew [math]\displaystyle{ A\,\! }[/math] arrives and completes the repair by 120.
- b) This repair uses the only spare part in inventory and triggers an on-condition restock. A part is ordered and is scheduled to arrive at 160.
- c) A scheduled restock part is also set to arrive at 150.
- d) Pool [on-hand = 0, pending: 150, 160].
- 2. Component [math]\displaystyle{ B\,\! }[/math] fails at 121. Crew [math]\displaystyle{ A\,\! }[/math] is available and it is engaged.
- a) Crew [math]\displaystyle{ A\,\! }[/math] arrives by 131 but no part is available.
- b) The failure finds the pool with no parts, triggering the on-condition restock. A part was ordered and is scheduled to arrive at 181.
- c) Pool [on-hand = 0, pending: 150, 160, 181].
- d) At 150, the first part arrives and is used by Component [math]\displaystyle{ B\,\! }[/math].
- e) Repair on Component [math]\displaystyle{ B\,\! }[/math] is completed 20 time units later, at 170.
- f) Pool [on-hand=0, pending: 160, 181].
- 3. Component [math]\displaystyle{ C\,\! }[/math] fails at 122. Crew [math]\displaystyle{ A\,\! }[/math] is already engaged by Component [math]\displaystyle{ B\,\! }[/math], thus Crew [math]\displaystyle{ B\,\! }[/math] is engaged.
- a) Crew [math]\displaystyle{ B\,\! }[/math] arrives at 137 but no part is available.
- b) The failure finds the pool with no parts, triggering the on-condition restock. A part is ordered and is scheduled to arrive at 182.
- c) Pool [on-hand = 0, pending: 160, 181,182].
- d) At 160, the part arrives and Component [math]\displaystyle{ C\,\! }[/math] is repaired by 180.
- e) Pool [on-hand = 0, pending: 181,182].
- 4. Component [math]\displaystyle{ F\,\! }[/math] fails at 123. No crews are available until 170 when Crew [math]\displaystyle{ A\,\! }[/math] becomes available.
- a) Crew [math]\displaystyle{ A\,\! }[/math] arrives by 180 and has to wait for a part.
- b) The failure found the pool with no parts, triggering the on-condition restock. A part is ordered and is scheduled to arrive at 183.
- c) Pool [on-hand = 0, pending: 181,182, 183].
- d) At 181, a part is obtained.
- e) By 201, the repair is completed.
- f) Pool [on-hand = 0, pending: 182, 183]
- 5. Component [math]\displaystyle{ D\,\! }[/math] fails at 171 with no crew available.
- a) Crew [math]\displaystyle{ B\,\! }[/math] becomes available at 180 and arrives by 195.
- b) The failure finds the pool with no parts, triggering the on-condition restock. A part is ordered and is scheduled to arrive at 231.
- c) The next part becomes available at 182 and the repair is completed by 205.
- d) Pool [on-hand = 0, pending: 183, 231]
- 6. End time is at 300. The last scheduled part arrives at the pool at 300.