Normal Confidence Bounds

Confidence Bounds

The method used by the application in estimating the different types of confidence bounds for normally distributed data is presented in this section. The complete derivations were presented in detail (for a general function) in Confidence Bounds.

Exact Confidence Bounds

There are closed-form solutions for exact confidence bounds for both the normal and lognormal distributions. However these closed-forms solutions only apply to complete data. To achieve consistent application across all possible data types, Weibull++ always uses the Fisher matrix method or likelihood ratio method in computing confidence intervals.

Fisher Matrix Confidence Bounds

Bounds on the Parameters

The lower and upper bounds on the mean, [math]\displaystyle{ \widehat{\mu }\,\! }[/math], are estimated from:

[math]\displaystyle{ \begin{align} & {{\mu }_{U}}= & \widehat{\mu }+{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })}\text{ (upper bound)} \\ & {{\mu }_{L}}= & \widehat{\mu }-{{K}_{\alpha }}\sqrt{Var(\widehat{\mu })}\text{ (lower bound)} \end{align}\,\! }[/math]

Since the standard deviation, [math]\displaystyle{ {{\widehat{\sigma }}}\,\! }[/math], must be positive, [math]\displaystyle{ \ln ({{\widehat{\sigma }}})\,\! }[/math] is treated as normally distributed, and the bounds are estimated from:

[math]\displaystyle{ \begin{align} & {{\sigma }_{U}}= & {{\widehat{\sigma }}}\cdot {{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}})}}{{{\widehat{\sigma }}}}}}\text{ (upper bound)} \\ & {{\sigma }_{L}}= & \frac{{{\widehat{\sigma }}}}{{{e}^{\tfrac{{{K}_{\alpha }}\sqrt{Var({{\widehat{\sigma }}})}}{{{\widehat{\sigma }}}}}}}\text{ (lower bound)} \end{align}\,\! }[/math]

where [math]\displaystyle{ {{K}_{\alpha }}\,\! }[/math] is defined by:

[math]\displaystyle{ \alpha =\frac{1}{\sqrt{2\pi }}\int_{{{K}_{\alpha }}}^{\infty }{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt=1-\Phi ({{K}_{\alpha }})\,\! }[/math]

If [math]\displaystyle{ \delta \,\! }[/math] is the confidence level, then [math]\displaystyle{ \alpha =\tfrac{1-\delta }{2}\,\! }[/math] for the two-sided bounds and [math]\displaystyle{ \alpha =1-\delta \,\! }[/math] for the one-sided bounds.

The variances and covariances of [math]\displaystyle{ \widehat{\mu }\,\! }[/math] and [math]\displaystyle{ {{\widehat{\sigma }}}\,\! }[/math] are estimated from the Fisher matrix, as follows:

[math]\displaystyle{ \left( \begin{matrix} \widehat{Var}\left( \widehat{\mu } \right) & \widehat{Cov}\left( \widehat{\mu },{{\widehat{\sigma }}} \right) \\ \widehat{Cov}\left( \widehat{\mu },{{\widehat{\sigma }}} \right) & \widehat{Var}\left( {{\widehat{\sigma }}} \right) \\ \end{matrix} \right)=\left( \begin{matrix} -\tfrac{{{\partial }^{2}}\Lambda }{\partial {{\mu }^{2}}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \mu \partial {{\sigma }}} \\ {} & {} \\ -\tfrac{{{\partial }^{2}}\Lambda }{\partial \mu \partial {{\sigma }}} & -\tfrac{{{\partial }^{2}}\Lambda }{\partial \sigma^{2}} \\ \end{matrix} \right)_{\mu =\widehat{\mu },\sigma =\widehat{\sigma }}^{-1}\,\! }[/math]

[math]\displaystyle{ \Lambda \,\! }[/math] is the log-likelihood function of the normal distribution, described in Parameter Estimation and Appendix D.

Bounds on Reliability

The reliability of the normal distribution is:

[math]\displaystyle{ \widehat{R}(t;\hat{\mu },{{\hat{\sigma }}})=\int_{t}^{\infty }\frac{1}{{{\widehat{\sigma }}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t-\widehat{\mu }}{{{\widehat{\sigma }}}} \right)}^{2}}}}dt\,\! }[/math]

Let [math]\displaystyle{ \widehat{z}=\tfrac{t-\widehat{\mu }}{{{\widehat{\sigma }}}}\,\! }[/math], the above equation then becomes:

[math]\displaystyle{ \hat{R}(\widehat{z})=\int_{\widehat{z}(t)}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\,\! }[/math]

The bounds on [math]\displaystyle{ z\,\! }[/math] are estimated from:

[math]\displaystyle{ \begin{align} & {{z}_{U}}= & \widehat{z}+{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \\ & {{z}_{L}}= & \widehat{z}-{{K}_{\alpha }}\sqrt{Var(\widehat{z})} \end{align}\,\! }[/math]

where:

[math]\displaystyle{ Var(\widehat{z})={{\left( \frac{\partial \hat{z}}{\partial \mu } \right)}^{2}}Var(\widehat{\mu })+{{\left( \frac{\partial \hat{z}}{\partial {{\sigma }}} \right)}^{2}}Var({{\widehat{\sigma }}})+2\left( \frac{\partial \hat{z}}{\partial \mu } \right)\left( \frac{\partial \hat{z}}{\partial {{\sigma }}} \right)Cov\left( \widehat{\mu },{{\widehat{\sigma }}} \right)\,\! }[/math]

or:

[math]\displaystyle{ Var(\widehat{z})=\frac{1}{\widehat{\sigma }^{2}}\left[ Var(\widehat{\mu })+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}})+2\cdot \widehat{z}\cdot Cov\left( \widehat{\mu },{{\widehat{\sigma }}} \right) \right]\,\! }[/math]

The upper and lower bounds on reliability are:

[math]\displaystyle{ \begin{align} & {{R}_{U}}= & \int_{{{z}_{L}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (upper bound)} \\ & {{R}_{L}}= & \int_{{{z}_{U}}}^{\infty }\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\text{ (lower bound)} \end{align}\,\! }[/math]

Bounds on Time

The bounds around time for a given normal percentile (unreliability) are estimated by first solving the reliability equation with respect to time, as follows:

[math]\displaystyle{ \hat{T}(\widehat{\mu },{{\widehat{\sigma }}})=\widehat{\mu }+z\cdot {{\widehat{\sigma }}}\,\! }[/math]

where:

[math]\displaystyle{ z={{\Phi }^{-1}}\left[ F(T) \right]\,\! }[/math]

and:

[math]\displaystyle{ \Phi (z)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{z}{{e}^{-\tfrac{1}{2}{{z}^{2}}}}dz\,\! }[/math]

The next step is to calculate the variance of [math]\displaystyle{ \hat{T}(\widehat{\mu },{{\widehat{\sigma }}})\,\! }[/math] or:

[math]\displaystyle{ \begin{align} Var(\hat{T})= & {{\left( \frac{\partial \hat{T}}{\partial \mu } \right)}^{2}}Var(\widehat{\mu })+{{\left( \frac{\partial \hat{T}}{\partial {{\sigma }}} \right)}^{2}}Var({{\widehat{\sigma }}}) \\ & +2\left( \frac{\partial \hat{T}}{\partial \mu } \right)\left( \frac{\partial \hat{T}}{\partial {{\sigma }}} \right)Cov\left( \widehat{\mu },{{\widehat{\sigma }}} \right) \\ Var(\hat{T})= & Var(\widehat{\mu })+{{\widehat{z}}^{2}}Var({{\widehat{\sigma }}})+2\cdot z\cdot Cov\left( \widehat{\mu },{{\widehat{\sigma }}} \right) \end{align}\,\! }[/math]

The upper and lower bounds are then found by:

[math]\displaystyle{ \begin{align} & {{T}_{U}}= & \hat{T}+{{K}_{\alpha }}\sqrt{Var(\hat{T})}\text{ (upper bound)} \\ & {{T}_{L}}= & \hat{T}-{{K}_{\alpha }}\sqrt{Var(\hat{T})}\text{ (lower bound)} \end{align}\,\! }[/math]

Likelihood Ratio Confidence Bounds

Bounds on Parameters

As covered in Confidence Bounds, the likelihood confidence bounds are calculated by finding values for [math]\displaystyle{ {{\theta }_{1}}\,\! }[/math] and [math]\displaystyle{ {{\theta }_{2}}\,\! }[/math] that satisfy:

[math]\displaystyle{ -2\cdot \text{ln}\left( \frac{L({{\theta }_{1}},{{\theta }_{2}})}{L({{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}})} \right)=\chi _{\alpha ;1}^{2}\,\! }[/math]

This equation can be rewritten as:

[math]\displaystyle{ L({{\theta }_{1}},{{\theta }_{2}})=L({{\widehat{\theta }}_{1}},{{\widehat{\theta }}_{2}})\cdot {{e}^{\tfrac{-\chi _{\alpha ;1}^{2}}{2}}}\,\! }[/math]

For complete data, the likelihood formula for the normal distribution is given by:

[math]\displaystyle{ L(\mu ,\sigma )=\underset{i=1}{\overset{N}{\mathop \prod }}\,f({{t}_{i}};\mu ,\sigma )=\underset{i=1}{\overset{N}{\mathop \prod }}\,\frac{1}{\sigma \cdot \sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{t}_{i}}-\mu }{\sigma } \right)}^{2}}}}\,\! }[/math]

where the [math]\displaystyle{ {{t}_{i}}\,\! }[/math] values represent the original time to failure data. For a given value of [math]\displaystyle{ \alpha \,\! }[/math], values for [math]\displaystyle{ \mu \,\! }[/math] and [math]\displaystyle{ \sigma \,\! }[/math] can be found which represent the maximum and minimum values that satisfy the above likelihood ratio equation. These represent the confidence bounds for the parameters at a confidence level [math]\displaystyle{ \delta \,\! }[/math], where [math]\displaystyle{ \alpha =\delta \,\! }[/math] for two-sided bounds and [math]\displaystyle{ \alpha =2\delta -1\,\! }[/math] for one-sided.

Example: LR Bounds on Parameters

Five units are put on a reliability test and experience failures at 12, 24, 28, 34, and 46 hours. Assuming a normal distribution, the MLE parameter estimates are calculated to be [math]\displaystyle{ \widehat{\mu }=28.8\,\! }[/math] and [math]\displaystyle{ \widehat{\sigma }=11.2143.\,\! }[/math] Calculate the two-sided 80% confidence bounds on these parameters using the likelihood ratio method.

Solution

The first step is to calculate the likelihood function for the parameter estimates:

[math]\displaystyle{ \begin{align} L(\widehat{\mu },\widehat{\sigma })= & \underset{i=1}{\overset{N}{\mathop \prod }}\,f({{t}_{i}};\widehat{\mu },\widehat{\sigma })=\underset{i=1}{\overset{5}{\mathop \prod }}\,\frac{1}{\widehat{\sigma }\cdot \sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{t}_{i}}-\widehat{\mu }}{\widehat{\sigma }} \right)}^{2}}}} \\ L(\widehat{\mu },\widehat{\sigma })= & \underset{i=1}{\overset{5}{\mathop \prod }}\,\frac{1}{11.2143\cdot \sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{t}_{i}}-28.8}{11.2143} \right)}^{2}}}} \\ L(\widehat{\mu },\widehat{\sigma })= & 4.676897\times {{10}^{-9}} \end{align}\,\! }[/math]

where [math]\displaystyle{ {{t}_{i}}\,\! }[/math] are the original time-to-failure data points. We can now rearrange the likelihood ratio equation to the form:

[math]\displaystyle{ L(\mu ,\sigma )-L(\widehat{\mu },\widehat{\sigma })\cdot {{e}^{\tfrac{-\chi _{\alpha ;1}^{2}}{2}}}=0\,\! }[/math]

Since our specified confidence level, [math]\displaystyle{ \delta \,\! }[/math], is 80%, we can calculate the value of the chi-squared statistic, [math]\displaystyle{ \chi _{0.8;1}^{2}=1.642374.\,\! }[/math] We can now substitute this information into the equation:

[math]\displaystyle{ \begin{align} L(\mu ,\sigma )-L(\widehat{\mu },\widehat{\sigma })\cdot {{e}^{\tfrac{-\chi _{\alpha ;1}^{2}}{2}}}= & 0, \\ \\ L(\mu ,\sigma )-4.676897\times {{10}^{-9}}\cdot {{e}^{\tfrac{-1.642374}{2}}}= & 0, \\ \\ L(\mu ,\sigma )-2.057410\times {{10}^{-9}}= & 0. \end{align}\,\! }[/math]

It now remains to find the values of [math]\displaystyle{ \mu \,\! }[/math] and [math]\displaystyle{ \sigma \,\! }[/math] which satisfy this equation. This is an iterative process that requires setting the value of [math]\displaystyle{ \mu \,\! }[/math] and finding the appropriate values of [math]\displaystyle{ \sigma \,\! }[/math], and vice versa.

The following table gives the values of [math]\displaystyle{ \sigma \,\! }[/math] based on given values of [math]\displaystyle{ \mu \,\! }[/math].

[math]\displaystyle{ \begin{matrix} \text{ }\!\!\mu\!\!\text{ } & {{\text{ }\!\!\sigma\!\!\text{ }}_{\text{1}}} & {{\text{ }\!\!\sigma\!\!\text{ }}_{\text{2}}} & \text{ }\!\!\mu\!\!\text{ } & {{\text{ }\!\!\sigma\!\!\text{ }}_{\text{1}}} & {{\text{ }\!\!\sigma\!\!\text{ }}_{\text{2}}} \\ \text{22}\text{.0} & \text{12}\text{.045} & \text{14}\text{.354} & \text{29}\text{.0} & \text{7.849}& \text{19.909} \\ \text{22}\text{.5} & \text{11}\text{.004} & \text{15}\text{.310} & \text{29}\text{.5} & \text{7}\text{.876} & \text{17}\text{.889} \\ \text{23}\text{.0} & \text{10}\text{.341} & \text{15}\text{.894} & \text{30}\text{.0} & \text{7}\text{.935} & \text{17}\text{.844} \\ \text{23}\text{.5} & \text{9}\text{.832} & \text{16}\text{.328} & \text{30}\text{.5} & \text{8}\text{.025} & \text{17}\text{.776} \\ \text{24}\text{.0} & \text{9}\text{.418} & \text{16}\text{.673} & \text{31}\text{.0} & \text{8}\text{.147} & \text{17}\text{.683} \\ \text{24}\text{.5} & \text{9}\text{.074} & \text{16}\text{.954} & \text{31}\text{.5} & \text{8}\text{.304} & \text{17}\text{.562} \\ \text{25}\text{.0} & \text{8}\text{.784} & \text{17}\text{.186} & \text{32}\text{.0} & \text{8}\text{.498} & \text{17}\text{.411} \\ \text{25}\text{.5} & \text{8}\text{.542} & \text{17}\text{.377} & \text{32}\text{.5} & \text{8}\text{.732} & \text{17}\text{.227} \\ \text{26}\text{.0} & \text{8}\text{.340} & \text{17}\text{.534} & \text{33}\text{.0} & \text{9}\text{.012} & \text{17}\text{.004} \\ \text{26}\text{.5} & \text{8}\text{.176} & \text{17}\text{.661} & \text{33}\text{.5} & \text{9}\text{.344} & \text{16}\text{.734} \\ \text{27}\text{.0} & \text{8}\text{.047} & \text{17}\text{.760} & \text{34}\text{.0} & \text{9}\text{.742} & \text{16}\text{.403} \\ \text{27}\text{.5} & \text{7}\text{.950} & \text{17}\text{.833} & \text{34}\text{.5} & \text{10}\text{.229} & \text{15}\text{.990} \\ \text{28}\text{.0} & \text{7}\text{.885} & \text{17}\text{.882} & \text{35}\text{.0} & \text{10}\text{.854} & \text{15}\text{.444} \\ \text{28}\text{.5} & \text{7}\text{.852} & \text{17}\text{.907} & \text{35}\text{.5} & \text{11}\text{.772} & \text{14}\text{.609} \\ \end{matrix}\,\! }[/math]

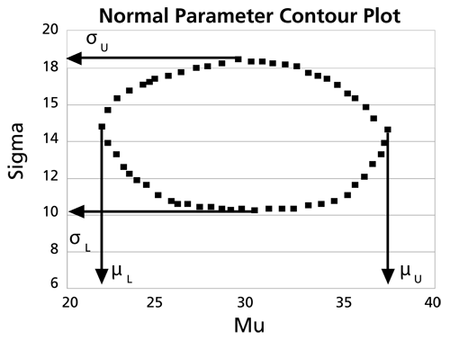
This data set is represented graphically in the following contour plot:

(Note that this plot is generated with degrees of freedom [math]\displaystyle{ k=1\,\! }[/math], as we are only determining bounds on one parameter. The contour plots generated in Weibull++ are done with degrees of freedom [math]\displaystyle{ k=2\,\! }[/math], for use in comparing both parameters simultaneously.) As can be determined from the table, the lowest calculated value for [math]\displaystyle{ \sigma \,\! }[/math] is 7.849, while the highest is 17.909. These represent the two-sided 80% confidence limits on this parameter. Since solutions for the equation do not exist for values of [math]\displaystyle{ \mu \,\! }[/math] below 22 or above 35.5, these can be considered the two-sided 80% confidence limits for this parameter. In order to obtain more accurate values for the confidence limits on [math]\displaystyle{ \mu \,\! }[/math], we can perform the same procedure as before, but finding the two values of [math]\displaystyle{ \mu \,\! }[/math] that correspond with a given value of [math]\displaystyle{ \sigma .\,\! }[/math] Using this method, we find that the two-sided 80% confidence limits on [math]\displaystyle{ \mu \,\! }[/math] are 21.807 and 35.793, which are close to the initial estimates of 22 and 35.5.

Bounds on Time and Reliability

In order to calculate the bounds on a time estimate for a given reliability, or on a reliability estimate for a given time, the likelihood function needs to be rewritten in terms of one parameter and time/reliability, so that the maximum and minimum values of the time can be observed as the parameter is varied. This can be accomplished by substituting a form of the normal reliability equation into the likelihood function. The normal reliability equation can be written as:

[math]\displaystyle{ R=1-\Phi \left( \frac{t-\mu }{\sigma } \right)\,\! }[/math]

This can be rearranged to the form:

[math]\displaystyle{ \mu =t-\sigma \cdot {{\Phi }^{-1}}(1-R)\,\! }[/math]

where [math]\displaystyle{ {{\Phi }^{-1}}\,\! }[/math] is the inverse standard normal. This equation can now be substituted into the likelihood ratio equation to produce an equation in terms of [math]\displaystyle{ \sigma ,\,\! }[/math] [math]\displaystyle{ t\,\! }[/math] and [math]\displaystyle{ R\,\! }[/math]:

[math]\displaystyle{ L(\sigma ,t/R)=\underset{i=1}{\overset{N}{\mathop \prod }}\,\frac{1}{\sigma \cdot \sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{t}_{i}}-\left[ t-\sigma \cdot {{\Phi }^{-1}}(1-R) \right]}{\sigma } \right)}^{2}}}}\,\! }[/math]

The unknown parameter [math]\displaystyle{ t/R\,\! }[/math] depends on what type of bounds are being determined. If one is trying to determine the bounds on time for a given reliability, then [math]\displaystyle{ R\,\! }[/math] is a known constant and [math]\displaystyle{ t\,\! }[/math] is the unknown parameter. Conversely, if one is trying to determine the bounds on reliability for a given time, then [math]\displaystyle{ t\,\! }[/math] is a known constant and [math]\displaystyle{ R\,\! }[/math] is the unknown parameter. The likelihood ratio equation can be used to solve the values of interest.

Example: LR Bounds on Time

For the same data set given above in the parameter bounds example, determine the two-sided 80% confidence bounds on the time estimate for a reliability of 40%. The ML estimate for the time at [math]\displaystyle{ R(t)=40%\,\! }[/math] is 31.637.

Solution

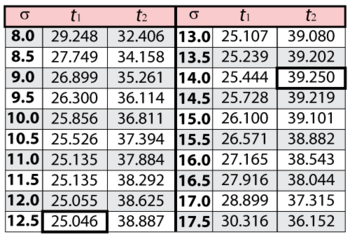
In this example, we are trying to determine the two-sided 80% confidence bounds on the time estimate of 31.637. This is accomplished by substituting [math]\displaystyle{ R=0.40\,\! }[/math] and [math]\displaystyle{ \alpha =0.8\,\! }[/math] into the likelihood ratio equation for the normal distribution, and varying [math]\displaystyle{ \sigma \,\! }[/math] until the maximum and minimum values of [math]\displaystyle{ t\,\! }[/math] are found. The following table gives the values of [math]\displaystyle{ t\,\! }[/math] based on given values of [math]\displaystyle{ \sigma \,\! }[/math].

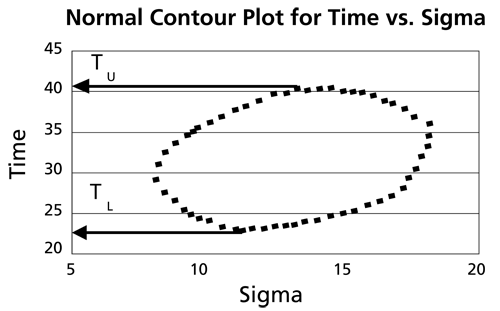
This data set is represented graphically in the following contour plot:

As can be determined from the table, the lowest calculated value for [math]\displaystyle{ t\,\! }[/math] is 25.046, while the highest is 39.250. These represent the 80% confidence limits on the time at which reliability is equal to 40%.

Example: LR Bounds on Reliability

For the same data set given above in the parameter bounds and time bounds examples, determine the two-sided 80% confidence bounds on the reliability estimate for [math]\displaystyle{ t=30\,\! }[/math]. The ML estimate for the reliability at [math]\displaystyle{ t=30\,\! }[/math] is 45.739%.

Solution

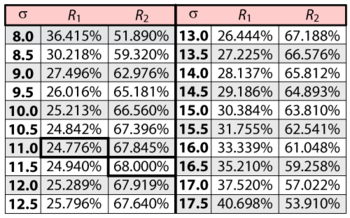
In this example, we are trying to determine the two-sided 80% confidence bounds on the reliability estimate of 45.739%. This is accomplished by substituting [math]\displaystyle{ t=30\,\! }[/math] and [math]\displaystyle{ \alpha =0.8\,\! }[/math] into the likelihood ratio equation for normal distribution, and varying [math]\displaystyle{ \sigma \,\! }[/math] until the maximum and minimum values of [math]\displaystyle{ R\,\! }[/math] are found. The following table gives the values of [math]\displaystyle{ R\,\! }[/math] based on given values of [math]\displaystyle{ \sigma \,\! }[/math].

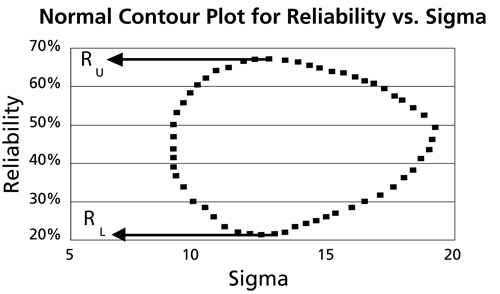
This data set is represented graphically in the following contour plot:

As can be determined from the table, the lowest calculated value for [math]\displaystyle{ R\,\! }[/math] is 24.776%, while the highest is 68.000%. These represent the 80% two-sided confidence limits on the reliability at [math]\displaystyle{ t=30\,\! }[/math].

Bayesian Confidence Bounds

Bounds on Parameters

From Confidence Bounds, we know that the marginal posterior distribution of [math]\displaystyle{ \mu \,\! }[/math] can be written as:

[math]\displaystyle{ \begin{align} f(\mu |Data)= & \int_{0}^{\infty }f(\mu ,\sigma |Data)d\sigma \\ = & \frac{\int_{0}^{\infty }L(Data|\mu ,\sigma )\varphi (\mu )\varphi (\sigma )d\sigma }{\int_{0}^{\infty }\int_{-\infty }^{\infty }L(Data|\mu ,\sigma )\varphi (\mu )\varphi (\sigma )d\mu d\sigma } \end{align}\,\! }[/math]

where:

[math]\displaystyle{ \varphi (\sigma )\,\! }[/math] = [math]\displaystyle{ \tfrac{1}{\sigma }\,\! }[/math] is the non-informative prior of [math]\displaystyle{ \sigma \,\! }[/math].

[math]\displaystyle{ \varphi (\mu )\,\! }[/math] is a uniform distribution from - [math]\displaystyle{ \infty \,\! }[/math] to + [math]\displaystyle{ \infty \,\! }[/math], the non-informative prior of [math]\displaystyle{ \mu .\,\! }[/math]

Using the above prior distributions, [math]\displaystyle{ f(\mu |Data)\,\! }[/math] can be rewritten as:

[math]\displaystyle{ f(\mu |Data)=\frac{\int_{0}^{\infty }L(Data|\mu ,\sigma )\tfrac{1}{\sigma }d\sigma }{\int_{0}^{\infty }\int_{-\infty }^{\infty }L(Data|\mu ,\sigma )\tfrac{1}{\sigma }d\mu d\sigma }\,\! }[/math]

The one-sided upper bound of [math]\displaystyle{ \mu \,\! }[/math] is:

[math]\displaystyle{ CL=P(\mu \le {{\mu }_{U}})=\int_{-\infty }^{{{\mu }_{U}}}f(\mu |Data)d\mu \,\! }[/math]

The one-sided lower bound of [math]\displaystyle{ \mu \,\! }[/math] is:

[math]\displaystyle{ 1-CL=P(\mu \le {{\mu }_{L}})=\int_{-\infty }^{{{\mu }_{L}}}f(\mu |Data)d\mu \,\! }[/math]

The two-sided bounds of [math]\displaystyle{ \mu \,\! }[/math] are:

[math]\displaystyle{ CL=P({{\mu }_{L}}\le \mu \le {{\mu }_{U}})=\int_{{{\mu }_{L}}}^{{{\mu }_{U}}}f(\mu |Data)d\mu \,\! }[/math]

The same method can be used to obtained the bounds of [math]\displaystyle{ \sigma \,\! }[/math].

Bounds on Time (Type 1)

The reliable life for the normal distribution is:

[math]\displaystyle{ \begin{align} T=\mu +\sigma {{\Phi }^{-1}}(1-R) \end{align}\,\! }[/math]

The one-sided upper bound on time is:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,(T\le {{T}_{U}})=\underset{}{\overset{}{\mathop{\Pr }}}\,(\mu +\sigma {{\Phi }^{-1}}(1-R)\le {{T}_{U}})\,\! }[/math]

The above equation can be rewritten in terms of [math]\displaystyle{ \mu \,\! }[/math] as:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,(\mu \le {{T}_{U}}-\sigma {{\Phi }^{-1}}(1-R))\,\! }[/math]

From the posterior distribution of [math]\displaystyle{ \mu\,\! }[/math]:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{-\infty }^{{{T}_{U}}-\sigma {{\Phi }^{-1}}(1-R)}L(\sigma ,\mu )\tfrac{1}{\sigma }d\mu d\sigma }{\int_{0}^{\infty }\int_{-\infty }^{\infty }L(\sigma ,\mu )\tfrac{1}{\sigma }d\mu d\sigma }\,\! }[/math]

The same method can be applied for one-sided lower bounds and two-sided bounds on time. 

Bounds on Reliability (Type 2)

The one-sided upper bound on reliability is:

[math]\displaystyle{ CL=\underset{}{\overset{}{\mathop{\Pr }}}\,(R\le {{R}_{U}})=\underset{}{\overset{}{\mathop{\Pr }}}\,(\mu \le T-\sigma {{\Phi }^{-1}}(1-{{R}_{U}}))\,\! }[/math]

From the posterior distribution of [math]\displaystyle{ \mu\,\! }[/math]:

[math]\displaystyle{ CL=\frac{\int_{0}^{\infty }\int_{-\infty }^{T-\sigma {{\Phi }^{-1}}(1-{{R}_{U}})}L(\sigma ,\mu )\tfrac{1}{\sigma }d\mu d\sigma }{\int_{0}^{\infty }\int_{-\infty }^{\infty }L(\sigma ,\mu )\tfrac{1}{\sigma }d\mu d\sigma }\,\! }[/math]

The same method can be used to calculate the one-sided lower bounds and the two-sided bounds on reliability.