 |
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.
|
Arrhenius-Lognormal Model for Interval Data with Activation Energy |
This example validates the results for the Arrhenius-lognormal model for interval data, with a given activation energy.
Reference Case
The data set is from Example 19.11 on page 508 in the book Statistical Methods for Reliability Data by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998.
Data
The data set for a new-technology IC Device is given below.
| Number in Group | Last Inspected (Hr) | State F/S | Time to State | Temperature (K) |
|---|---|---|---|---|
| 50 | 788 | S | 1536 | 423.15 |
| 50 | 788 | S | 1536 | 448.15 |
| 50 | 96 | S | 96 | 473.15 |
| 1 | 384 | F | 788 | 523.15 |
| 3 | 788 | F | 1536 | 523.15 |
| 5 | 1536 | F | 2304 | 523.15 |
| 41 | 1536 | S | 2304 | 523.15 |
| 4 | 192 | F | 384 | 573.15 |
| 27 | 384 | F | 788 | 573.15 |
| 16 | 788 | F | 1536 | 573.15 |
| 3 | 788 | S | 1536 | 573.15 |
Result
The following function is used for the Ln-Mean [math]\displaystyle{ \mu'\,\! }[/math] of the lognormal distribution:
where T is the temperature; [math]\displaystyle{ \beta_{1}\,\! }[/math] is the activation energy; and 11605 is calculated from the reciprocal of the Boltzmann constant. This function can be written in the following way:
The above equation is the general log-linear model in ALTA. In ALTA, the coefficients are denoted by [math]\displaystyle{ \alpha_{i}\,\! }[/math]. We can see [math]\displaystyle{ \beta_{0} = \alpha_{0}\,\! }[/math] and [math]\displaystyle{ \beta_{1} = \frac{\alpha_{1}}{11605}\,\! }[/math].
In fact, the above model can also be expressed using the traditional Arrhenius model:
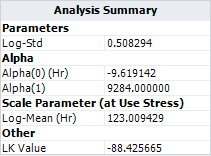
In the book, the activation energy is assumed to be known. So [math]\displaystyle{ \beta_{1} = 0.8 eV\,\! }[/math], or [math]\displaystyle{ \alpha_{1} = 0.8 \times 11605 = 9284\,\! }[/math] .
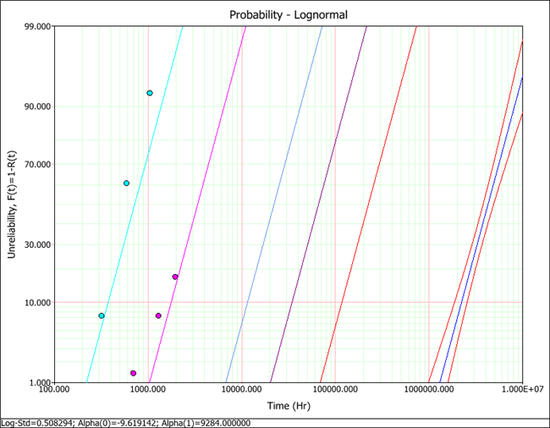
No results are provided in the book. Only the probability plot is given in Figure 19.15. The plot shows that the confidence interval for the reliability at the use stress of 100°C is very narrow.
Results in ALTA
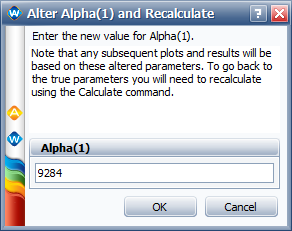
We can use the "Alter One Parameter (and Recalculate)" utility in ALTA to enter the value for [math]\displaystyle{ \alpha_{1}\,\! }[/math] = 9284, as shown next.
The following picture shows the results.
The probability plot with confidence interval at the use temperature level is shown next. This plot is similar to the plot shown in the book. The confidence interval for the reliability at the use stress level (the line at the far right side of the plot) is very tight since the activation energy is given.
