Parallel Systems RBD
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at BlockSim examples and BlockSim reference examples.
|
Parallel Systems RBD |
This example validates the results for parallel systems in BlockSim's analytical and simulation diagrams.
Reference Case
The data set is from example 4.6 on page 73 in the book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.
Data
A lighting system uses three identical bulbs. The lifetimes of the bulbs are assumed to follow a 2-paremeter Weibull with parameters α = 35,800 hours (this is the eta value in BlockSim) and β = 1.35. We calculate the reliability of the system after 8760 hours of use, and the number of bulbs needed to be connected in parallel to achieve 99.99% reliability at that time.
Result
Since the lives of the bulbs are modeled with the Weibull distribution, the reliability of a single bulb is calculated as:
- [math]\displaystyle{ R_{0} = exp \left [ -\left(\frac{t}{\lambda}\right)^{\beta} \right ] = exp\left [ -\left(\frac{8,760}{35,800}\right)^{1.35} \right ] = 0.8611\,\! }[/math]
Substituting the value of R0 into Equation 4.11 on page 72:
- [math]\displaystyle{ R = 1 - (1-R_{0})^{n}\,\! }[/math]
where R is the system reliability and n is the number of identical components that form the system. The reliability of the system can be calculated as:
- [math]\displaystyle{ R = 1 - (1-0.8611)^{3} = 0.9973\,\! }[/math]
The minimum number of bulbs required to achieve 99.99% reliability after 8760 hours of use can be calculated via Equation 4.12 on page 72.
- [math]\displaystyle{ n = \frac{ln(1-R)}{ln(1-R_{0})} = \frac{ln(1-0.9999)}{ln(1-0.8611)} = 4.6658\,\! }[/math]
Therefore, a minimum of 5 bulbs in parallel configuration are needed to achieve 99.99% reliability.
Results in BlockSim
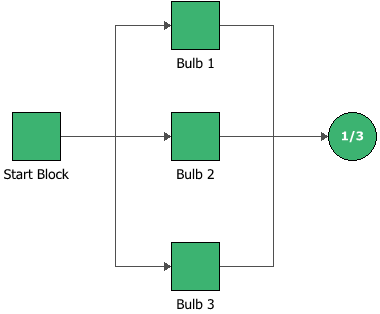
In BlockSim, the lighting system RBD is configured as shown below.
Each bulb is modeled with a 2-parameter Weibull distribution with parameters eta = 35,800 hours and beta = 1.35.
Analytical Proof
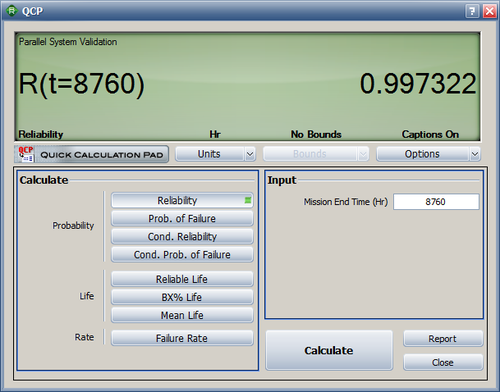
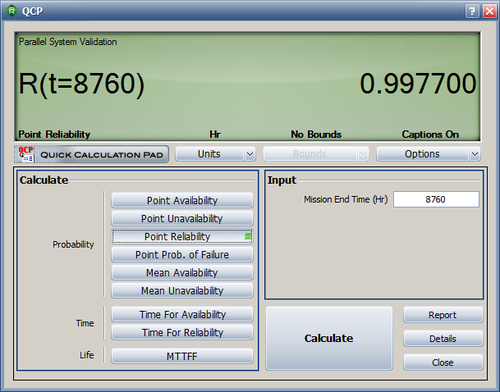
The reliability after 8760 hours of use is estimated to be 99.73%, which is the same result as calculated in the reference book.
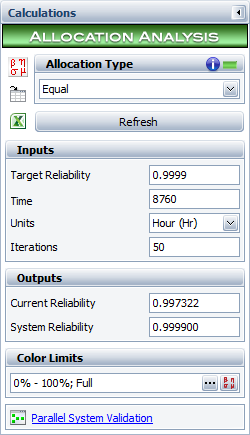
The minimum number of bulbs required to achieve 99.99% reliability after 8760 hours of use can be estimated via the Allocation Analysis tool.
The analysis shows that the number of bulbs needs to be increased to 1.55506. Therefore, the total number of bulbs needed in parallel to achieve 99.99% reliability after 8760 hours of use is 4.66518 bulbs, which is the sum of the "Equivalent Parallel Units" column shown below. This number is almost exactly the same as the one calculated in the reference book.
Simulation Proof
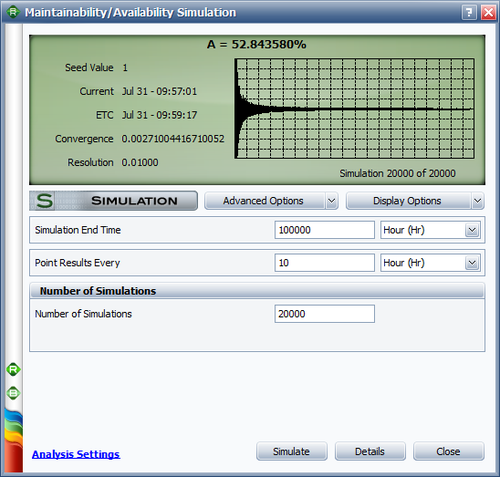
We can also estimate the results by using the simulation tool in BlockSim. The simulation settings are shown below.
The point reliability after 8760 hours of use is estimated to be 99.77%.