New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.
|
General Log-Linear (GLL)-Weibull Model
|
This example compares the results for the GLL life-stress relationship with a Weibull distribution.
Reference Case
The data set is from Example 7.14 on page 297 in book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.
Data
The following table shows the data.
| State F/S
|
Time to State (Hr)
|
Temperature (°C)
|
Group ID
|
| F |
1138 |
100 |
1
|
| F |
1944 |
100 |
1
|
| F |
2764 |
100 |
1
|
| F |
2846 |
100 |
1
|
| F |
3246 |
100 |
1
|
| F |
3803 |
100 |
1
|
| F |
5046 |
100 |
1
|
| F |
5139 |
100 |
1
|
| S |
5500 |
100 |
1
|
| S |
5500 |
100 |
1
|
| S |
5500 |
100 |
1
|
| S |
5500 |
100 |
1
|
| F |
1121 |
120 |
2
|
| F |
1572 |
120 |
2
|
| F |
2329 |
120 |
2
|
| F |
2573 |
120 |
2
|
| F |
2702 |
120 |
2
|
| F |
3702 |
120 |
2
|
| F |
4277 |
120 |
2
|
| S |
4500 |
120 |
2
|
| F |
420 |
150 |
3
|
| F |
650 |
150 |
3
|
| F |
703 |
150 |
3
|
| F |
838 |
150 |
3
|
| F |
1086 |
150 |
3
|
| F |
1125 |
150 |
3
|
| F |
1387 |
150 |
3
|
| F |
1673 |
150 |
3
|
| F |
1896 |
150 |
3
|
| F |
2037 |
150 |
3
|
Result
The model used in the book is:
- [math]\displaystyle{ \,\!ln\left ( \eta \right )=\alpha _{0}+\alpha _{1}\frac{1}{T} }[/math]
The book has the following results:
- The model parameters are: [math]\displaystyle{ \,\!\alpha _{0}=-3.156 }[/math] , [math]\displaystyle{ \,\!\alpha _{1}=4390 }[/math] and [math]\displaystyle{ \,\!\beta =2.27 }[/math].
- The variance of each parameter is: [math]\displaystyle{ \,\!Var\left ( \alpha _{0} \right )=3.08 }[/math] , [math]\displaystyle{ \,\!Var\left ( \alpha _{1} \right )=484819.5 }[/math] and [math]\displaystyle{ \,\!Var\left ( \beta\right )=0.1396 }[/math] .
- The two-sided 90% confidence intervals for the model parameters are: [math]\displaystyle{ \,\!\left [ \alpha _{0,L},\alpha _{0,U} \right ]=\left [ -6.044, -0.269 \right ] }[/math] , [math]\displaystyle{ \,\!\left [ \alpha _{1,L},\alpha _{1,U} \right ]=\left [ 3244.8, 5535.3 \right ] }[/math] and [math]\displaystyle{ \,\!\left [ \beta _{1,L},\beta _{1,U} \right ]=\left [ 1.73, 2.97 \right ] }[/math] .
- The estimated B10 life at temperature of 35°C is 24,286 hours. The two-sided 90% confidence interval is [10371, 56867].
- The estimated reliability at 35°C and 10,000 hours is [math]\displaystyle{ \,\!R\left ( 10000 \right )=0.9860 }[/math] . The two-sided 90% confidence interval is [0.892, 0.998].
Results in ALTA
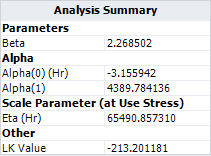
In ALTA, the GLL model with Weibull distribution is used. Since temperature is the stress, the reciprocal transform is used. The results are:
- The model parameters are:
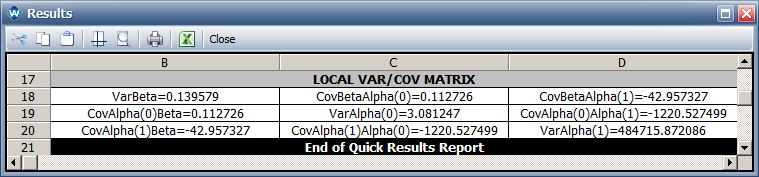
- The variances of the parameters are:
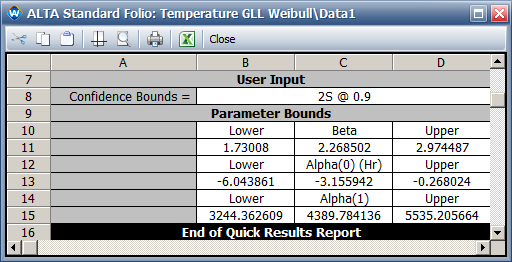
- The two-sided 90% confidence intervals for the model parameters are:
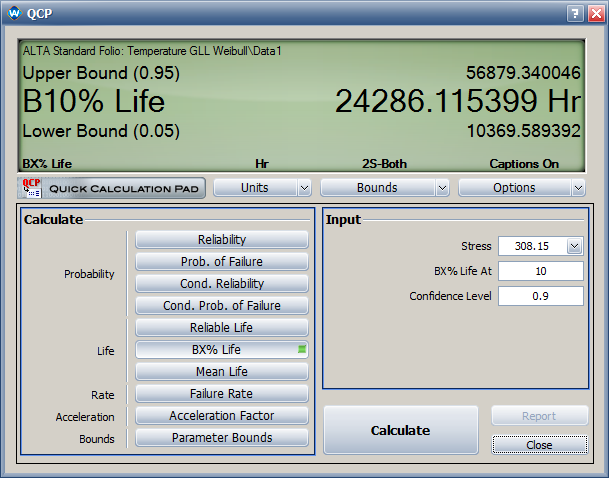
- The estimated B10 life and its two-sided 90% confidence intervals are:
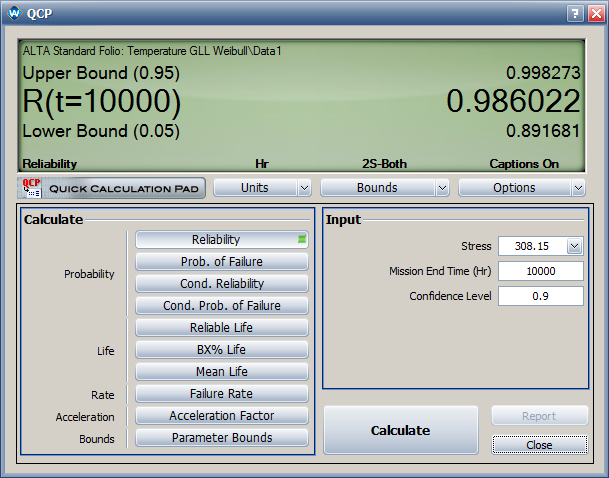
- The estimated reliability with its two-sided 90% confidence interval at 35°C and 10,000 hours are: