Two Level Optimum Test Plan for One Stress
ALTA_Reference_Examples_Banner.png
|
ALTA_Reference_Examples |
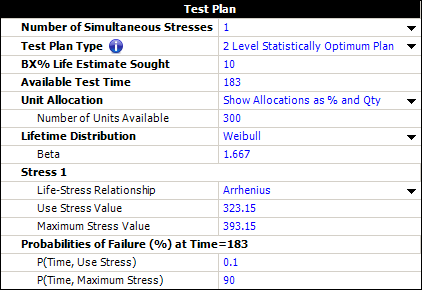
This example compares the results for the 2-Level Statistically Optimum test plan for one stress.
Reference Case
The data set is from Example 20.5 on page 542 in the book Statistical Methods for Reliability Data by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998.
Data
A Weibull distribution with Arrhenius relationship is used. The Arrhenius relationship uses the following formula
- [math]\displaystyle{ ln(\eta) = \beta_{0} + \beta_{1} \times \frac{11605}{T}\,\! }[/math]
The planning values of the model parameters used in the test plan are [math]\displaystyle{ \beta\,\! }[/math] = 1.667, [math]\displaystyle{ \beta_{0}\,\! }[/math] = -16.7333 and [math]\displaystyle{ \beta_{1}\,\! }[/math] = 0.7265. These planning values were obtained based on the following assumptions: 0.1% of the units will fail in 6 months (183 hours) at 50°C, and 90% would fail in 6 months at 120°C. This information is given in Example 20.2 on page 535.
The use temperature is 50°C (323.15°K) and the highest temperature used in the test is 120°C (393.15 °K).
A total of 300 units are available for testing. Three temperature levels can be used and 20% of the units will be tested at the middle temperature level. The objective of the test plan is to:
- Determine the two temperature levels that can be used in the test.
- Determine the number of test units at each temperature level.
Tests will be conducted using the created test plan. The failure data from the test is then used to estimate the model parameters. The estimated parameters are used to calculate the B10 life at 50°C and its variance.
We need to find a test plan with three temperature levels that will minimize the estimation variance for the B10 life at 50°C.
Result
The two level statistically optimum test plan is: 212 units will be tested at 95°C (368.15 °K), and 88 units will be tested at 120°C (393.15 °K). The estimated standard error for the B10 life at 50°C from this test plan is [math]\displaystyle{ Ase\left [log \left(\hat{t}_{0.1}(50) \right) \right] = 0.3794\,\! }[/math].
Results in ALTA
The planning information is entered in ALTA, as shown below.
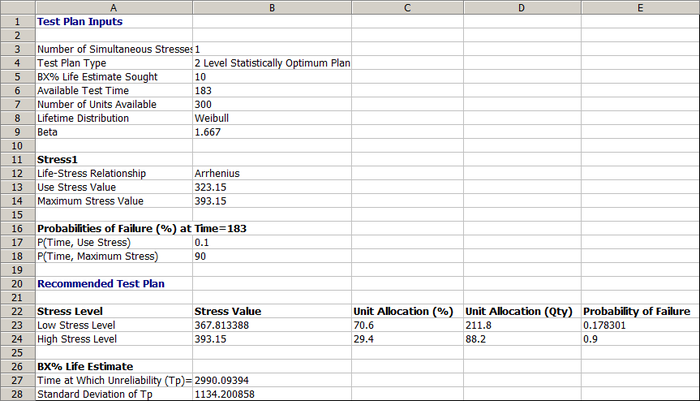
The resulting 2-level statistically optimum test plan in ALTA is shown below.
The test plan shows that:
- The low stress level (row 23) should be 367.8°K (94.65°C) and about 212 units should be tested at this temperature.
- The high stress level (row 24) should be 393.15°K (120°C) and about 88 units should be tested at this temperature.
The results above are the same as the results given in the book.
The estimated standard deviation of the log B10 life at 50°C can be calculate using the BX% Life Estimate result in the output from ALTA (row 26), as given below:
- [math]\displaystyle{ Ase\left[log \left(\hat{t}_{0.1}(50) \right) \right] = \frac{Ase\hat{t}_{0.1}(50)}{\hat{t}_{0.1}(50)} = \frac{1134.2}{2990.09} = 0.37932\,\! }[/math]
This is very close to the estimated standard deviation in the book. The difference is probably caused by the rounding error.