Degradation Data Analysis with a Power Regression Model
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
|
Degradation Data Analysis with a Power Regression Model |
This example compares the results for a degradation analysis with a power regression model.
Reference Case
The data set is from Example 8.1 on page 336 in the book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.
Data
The following table shows the percent transconductance degradation data taken at different times for five units of a MOS field-effect transistor. The failure criterion is defined as a degradation greater than or equal to 15%.
| Time | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 100 | 1.05 | 0.58 | 0.86 | 0.6 | 0.62 |
| 200 | 1.4 | 0.9 | 1.25 | 0.6 | 0.64 |
| 300 | 1.75 | 1.2 | 1.45 | 0.6 | 1.25 |
| 400 | 2.1 | 1.75 | 1.75 | 0.9 | 1.3 |
| 500 | 2.1 | 2.01 | 1.75 | 0.9 | 0.95 |
| 600 | 2.8 | 2 | 2 | 1.2 | 1.25 |
| 700 | 2.8 | 2 | 2 | 1.5 | 1.55 |
| 800 | 2.8 | 2 | 2 | 1.5 | 1.9 |
| 900 | 3.2 | 2 | 2.3 | 1.5 | 1.25 |
| 1000 | 3.4 | 2.3 | 2.3 | 1.7 | 1.55 |
| 1200 | 3.8 | 2.6 | 2.6 | 2.1 | 1.5 |
| 1400 | 4.2 | 2.9 | 2.8 | 2.1 | 1.55 |
| 1600 | 4.2 | 3.2 | 3.15 | 1.8 | 1.9 |
| 1800 | 4.5 | 3.6 | 3.2 | 2.1 | 1.85 |
| 2000 | 4.9 | 3.8 | 3.2 | 2.1 | 2.2 |
| 2500 | 5.6 | 4.2 | 3.8 | 2.4 | 2.2 |
| 3000 | 5.9 | 4.4 | 3.8 | 2.7 | 2.5 |
| 3500 | 6.3 | 4.8 | 4 | 2.7 | 2.2 |
| 4000 | 6.6 | 5 | 4.2 | 3 | 2.8 |
| 4500 | 7 | 5.6 | 4.4 | 3 | 2.8 |
| 5000 | 7.8 | 5.9 | 4.6 | 3 | 2.8 |
| 6000 | 8.6 | 6.2 | 4.9 | 3.6 | 3.1 |
| 7000 | 9.1 | 6.8 | 5.2 | 3.6 | 3.1 |
| 8000 | 9.5 | 7.4 | 5.8 | 4.2 | 3.1 |
| 9000 | 10.5 | 7.7 | 6.1 | 4.6 | 3.7 |
| 10000 | 11.1 | 8.4 | 6.3 | 4.2 | 4.4 |
| 12000 | 12.2 | 8.9 | 7 | 4.8 | 3.7 |
| 14000 | 13 | 9.5 | 7.2 | 5.1 | 4.4 |
| 16000 | 14 | 10 | 7.6 | 4.8 | 4.4 |
| 18000 | 15 | 10.4 | 7.7 | 5.3 | 4.1 |
| 20000 | 16 | 10.9 | 8.1 | 5.8 | 4.1 |
| 25000 | 18.5 | 12.6 | 8.9 | 5.7 | 4.7 |
| 30000 | 20.3 | 13.2 | 9.5 | 6.2 | 4.7 |
| 35000 | 22.1 | 15.4 | 11.2 | 8 | 6.4 |
| 40000 | 24.2 | 18.1 | 14 | 10.9 | 9.4 |
Result
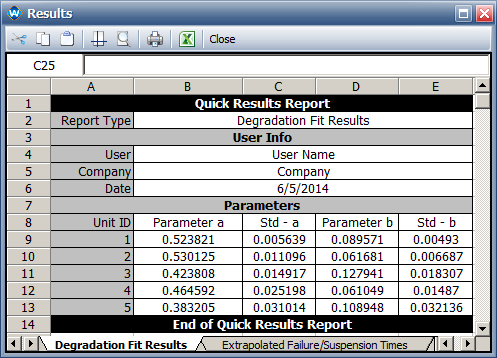
In the book, the following equation is used: [math]\displaystyle{ ln(y) = \beta_{1} + \beta_{2} ln(t)\,\! }[/math]. It in fact is a power equation [math]\displaystyle{ y = bt^{a}\,\! }[/math] with [math]\displaystyle{ ln(b) = \beta_{1}\,\! }[/math] and [math]\displaystyle{ a = \beta_{2}\,\! }[/math]. This degradation equation is used for each test unit to predict the pseudo failure time, and then a lognormal distribution is used to model the pseudo failure times. The results are:
- For the power regression model
- For unit 1 [math]\displaystyle{ \beta_{1}\,\! }[/math] = -2.413 , [math]\displaystyle{ \beta_{2}\,\! }[/math] = 0.524
- For unit 2 [math]\displaystyle{ \beta_{1}\,\! }[/math] = -2.735 , [math]\displaystyle{ \beta_{2}\,\! }[/math] = 0.525
- For unit 3 [math]\displaystyle{ \beta_{1}\,\! }[/math] = -2.056 , [math]\displaystyle{ \beta_{2}\,\! }[/math] = 0.424
- For unit 4 [math]\displaystyle{ \beta_{1}\,\! }[/math] = -2.796 , [math]\displaystyle{ \beta_{2}\,\! }[/math] = 0.465
- For unit 5 [math]\displaystyle{ \beta_{1}\,\! }[/math] = -2.217 , [math]\displaystyle{ \beta_{2}\,\! }[/math] = 0.383
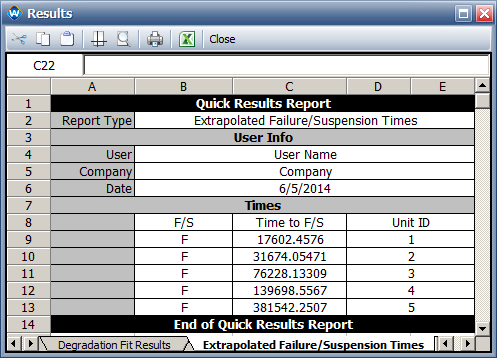
- The predicted pseudo failure times: 17,553; 31,816; 75,809; 138,229.
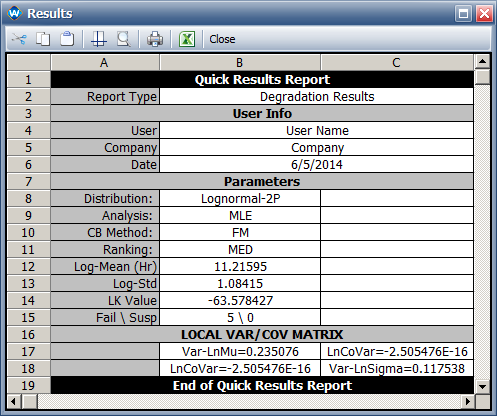
- The fitted lognormal distribution: Ln-Mean = 11.214, Ln-Std = 1.085.
Results in Weibull++
- For the power regression model:
- The predicted pseudo failure times:
- The fitted lognormal distribution: