New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
|
Gamma Distribution with MLE Solution
|
This example compares the MLE solution for the Gamma distribution.
Reference Case
The data from Table 1.1 on page 4 in the book Statistical Methods for Reliability Data by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998 is used.
Data
| Failures
|
| 17.88 |
28.92 |
33
|
| 41.52 |
42.12 |
45.6
|
| 48.4 |
51.84 |
51.96
|
| 54.12 |
55.56 |
67.8
|
| 68.64 |
68.64 |
68.88
|
| 84.12 |
93.12 |
98.64
|
| 105.12 |
105.84 |
127.92
|
| 128.04 |
173.4 |
|
Result
The solution is given on page 257, Example 11.1. The ML estimates are [math]\displaystyle{ \theta \,\! }[/math] = 17.94, k = 4.025.
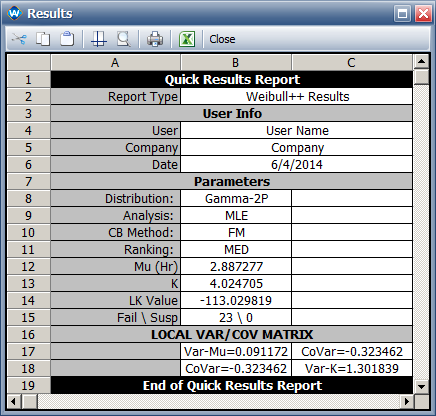
Results in Weibull++
In Weibull++, the parameter [math]\displaystyle{ \mu\,\! }[/math] is used instead of [math]\displaystyle{ \theta \,\! }[/math]. The relation between them is [math]\displaystyle{ \theta = exp(\mu)\,\! }[/math].
We can see [math]\displaystyle{ \mu\,\! }[/math] = 2.8873. Therefore, [math]\displaystyle{ \theta = exp(\mu)\,\! }[/math] = 17.94, which is the same as the results in the book.