Resolution III Design Example
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at DOE examples and DOE reference examples.
This example appears in the Design and Analysis Reference book.
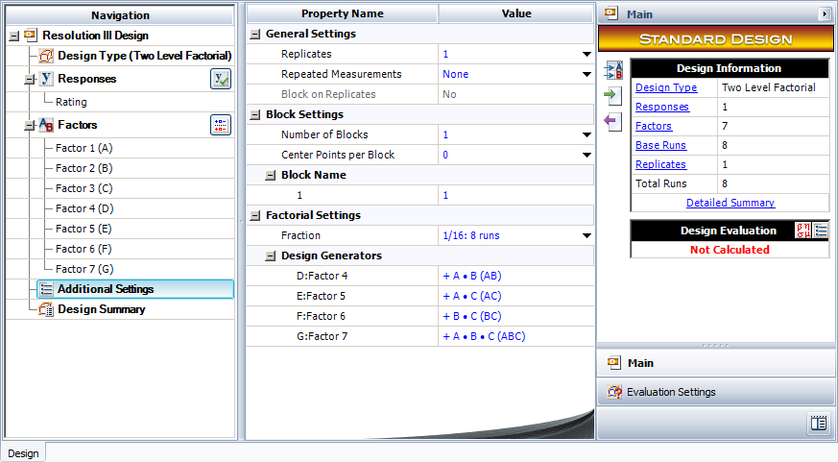
A baker wants to investigate the factors that most affect the taste of the cakes made in his bakery. He chooses to investigate seven factors, each at two levels: flour type (factor [math]\displaystyle{ A\,\! }[/math]), conditioner type (factor [math]\displaystyle{ B\,\! }[/math]), sugar quantity (factor [math]\displaystyle{ C\,\! }[/math]), egg quantity (factor [math]\displaystyle{ D\,\! }[/math]), preservative type (factor [math]\displaystyle{ E\,\! }[/math]), bake time (factor [math]\displaystyle{ F\,\! }[/math]) and bake temperature (factor [math]\displaystyle{ G\,\! }[/math]). The baker expects most of these factors and all higher order interactions to be inactive. On the basis of this, he decides to run a screening experiment using a 2 [math]\displaystyle{ _{\text{III}}^{7-4}\,\! }[/math] design that requires just 8 runs. The cakes are rated on a scale of 1 to 10. The design properties for the 2 [math]\displaystyle{ _{\text{III}}^{7-4}\,\! }[/math] design (with generators [math]\displaystyle{ D=AB\,\! }[/math], [math]\displaystyle{ E=AC\,\! }[/math], [math]\displaystyle{ F=BC\,\! }[/math] and [math]\displaystyle{ G=ABC\,\! }[/math]) are shown in the following figure.
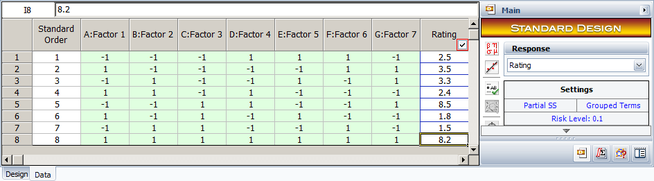
The resulting design along with the rating of the cakes corresponding to each run is shown in the following figure.
The normal probability plot of effects for the unreplicated design shows main effects [math]\displaystyle{ B\,\! }[/math], [math]\displaystyle{ C\,\! }[/math], [math]\displaystyle{ D\,\! }[/math] and [math]\displaystyle{ G\,\! }[/math] to be significant, as shown in the next figure.
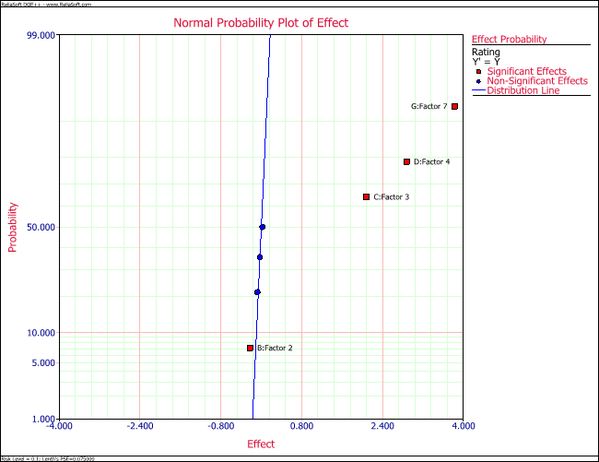
However, for this design, the following alias relations exist for the main effects:
Based on the alias structure, three separate possible conclusions can be drawn. It can be concluded that effect [math]\displaystyle{ CD\,\! }[/math] is active instead of [math]\displaystyle{ G\,\! }[/math] so that effects [math]\displaystyle{ C\,\! }[/math], [math]\displaystyle{ D\,\! }[/math] and their interaction, [math]\displaystyle{ CD\,\! }[/math], are the significant effects. Another conclusion can be that effect [math]\displaystyle{ DG\,\! }[/math] is active instead of [math]\displaystyle{ C\,\! }[/math] so that effects [math]\displaystyle{ D\,\! }[/math], [math]\displaystyle{ G\,\! }[/math] and their interaction, [math]\displaystyle{ DG\,\! }[/math], are significant. Yet another conclusion can be that effects [math]\displaystyle{ C\,\! }[/math], [math]\displaystyle{ G\,\! }[/math] and their interaction, [math]\displaystyle{ CG\,\! }[/math], are significant. To accurately discover the active effects, the baker decides to a run a fold-over of the present design and base his conclusions on the effect values calculated once results from both the designs are available.
The present design is shown next.
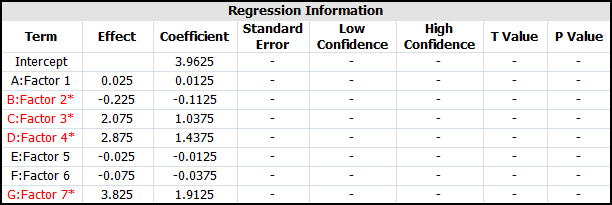
Using the alias relations, the effects obtained from DOE++ for the present design can be expressed as:
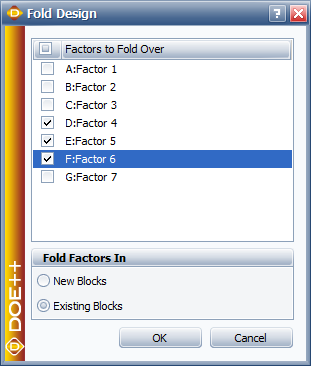
The fold-over design for the experiment is obtained by reversing the signs of the columns [math]\displaystyle{ D\,\! }[/math], [math]\displaystyle{ E\,\! }[/math], and [math]\displaystyle{ F\,\! }[/math]. In DOE++, you can fold over a design using the following window.
The resulting design and the corresponding response values obtained are shown in the following figures.
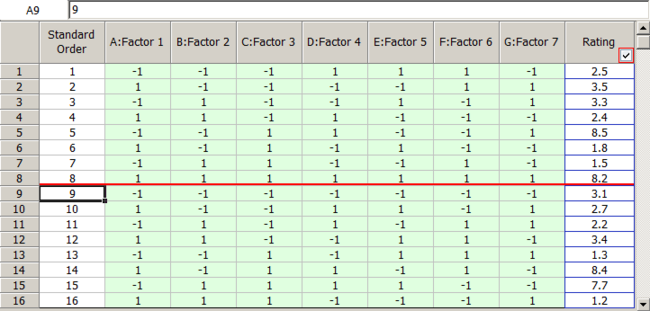
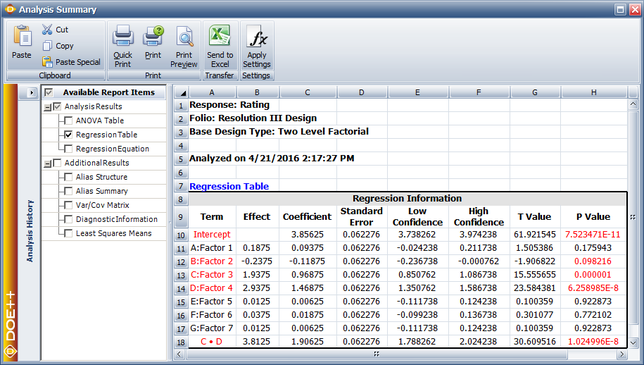
Comparing the absolute values of the effects, the active effects are [math]\displaystyle{ B\,\! }[/math], [math]\displaystyle{ C\,\! }[/math], [math]\displaystyle{ D\,\! }[/math] and the interaction [math]\displaystyle{ CD\,\! }[/math]. Therefore, the most important factors affecting the taste of the cakes in the present case are sugar quantity, egg quantity and their interaction.