Concurrent Operating Times - Crow-AMSAA (NHPP) Example

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.

---

This example appears in the Reliability Growth and Repairable System Analysis Reference book.

Six systems were subjected to a reliability growth test, and a total of 82 failures were observed. Given the data in the table below, which presents the start/end times and times-to-failure for each system, do the following:

1. Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
2. Determine how many additional failures would be generated if testing continues until 3,000 hours.

Multiple Systems (Concurrent Operating Times) Data

System #	1	2	3	4	5	6
Start Time (Hr)	0	0	0	0	0	0
End Time (Hr)	504	541	454	474	436	500
Failure Times (Hr)	21	83	26	36	23	7
	29	83	26	306	46	13
	43	83	57	306	127	13
	43	169	64	334	166	31
	43	213	169	354	169	31
	66	299	213	395	213	82
	115	375	231	403	213	109
	159	431	231	448	255	137
	199		231	456	369	166
	202		231	461	374	200
	222		304		380	210
	248		383		415	220
	248					301
	255					422
	286					437
	286					469
	304					469
	320
	348
	364
	404
	410
	429

Solution

1. To estimate the parameters [math]\displaystyle{ \hat{\beta }\,\! }[/math] and [math]\displaystyle{ \hat{\lambda}\,\! }[/math], the equivalent single system (ESS) must first be determined. The ESS is given below:

Equivalent Single System

Row	Time to Event (hr)		Row	Time to Event (hr)		Row	Time to Event (hr)		Row	Time to Event (hr)
1	42		22	498		43	1386		64	2214
2	78		23	654		44	1386		65	2244
3	78		24	690		45	1386		66	2250
4	126		25	762		46	1386		67	2280
5	138		26	822		47	1488		68	2298
6	156		27	954		48	1488		69	2370
7	156		28	996		49	1530		70	2418
8	174		29	996		50	1530		71	2424
9	186		30	1014		51	1716		72	2460
10	186		31	1014		52	1716		73	2490
11	216		32	1014		53	1794		74	2532
12	258		33	1194		54	1806		75	2574
13	258		34	1200		55	1824		76	2586
14	258		35	1212		56	1824		77	2621
15	276		36	1260		57	1836		78	2676
16	342		37	1278		58	1836		79	2714
17	384		38	1278		59	1920		80	2734
18	396		39	1278		60	2004		81	2766
19	492		40	1278		61	2088		82	2766
20	498		41	1320		62	2124
21	498		42	1332		63	2184

Given the ESS data, the value of [math]\displaystyle{ \hat{\beta }\,\! }[/math] is calculated using:

[math]\displaystyle{ \hat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}}\,\! }[/math]

[math]\displaystyle{ \hat{\beta }=0.8939\,\! }[/math]

where [math]\displaystyle{ n\,\! }[/math] is the number of failures and [math]\displaystyle{ T^*\,\! }[/math] is the termination time. The termination time is the sum of end times for each of the systems which equals 2909.

[math]\displaystyle{ \hat{\lambda}\,\! }[/math] is estimated with:

[math]\displaystyle{ \hat{\lambda }=\frac{n}{{{T}^{*}}^{\beta }} }[/math]

[math]\displaystyle{ \hat{\lambda }=0.0657\,\! }[/math]

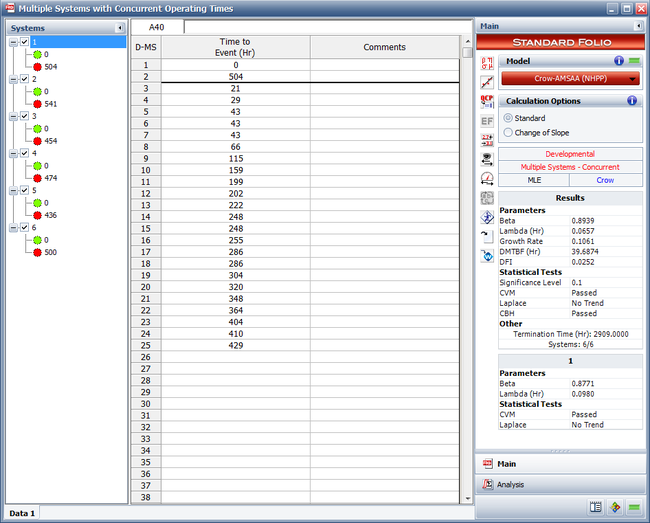
The next figure shows the parameters estimated using RGA.

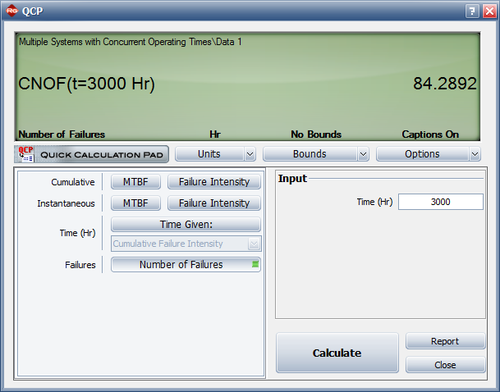
2. The number of failures can be estimated using the Quick Calculation Pad, as shown next. The estimated number of failures at 3,000 hours is equal to 84.2892 and 82 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3,000 hours is equal to [math]\displaystyle{ 84.2892-82=2.2892\approx 3\,\! }[/math]