Template:Example: Recurrent Events Data Non-parameteric MCF Bound Example

Recurrent Events Data Non-parameteric MCF Bound Example

Using the data in Example 1, estimate the 95% confidence bounds.

Solution

Using MCF variance equation the following table of variance values can be obtained:

ID	Months	State	[math]\displaystyle{ r_i }[/math]	[math]\displaystyle{ Var_i }[/math]
1	5	F	5	[math]\displaystyle{ (\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.032 }[/math]
2	6	F	5	[math]\displaystyle{ 0.032+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.064 }[/math]
1	10	F	5	[math]\displaystyle{ 0.064+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.096 }[/math]
3	12	F	5	[math]\displaystyle{ 0.096+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.128 }[/math]
2	13	F	5	[math]\displaystyle{ 0.128+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.160 }[/math]
4	13	F	5	[math]\displaystyle{ 0.160+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.192 }[/math]
1	15	F	5	[math]\displaystyle{ 0.192+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.224 }[/math]
4	15	F	5	[math]\displaystyle{ 0.224+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.256 }[/math]
5	16	F	5	[math]\displaystyle{ 0.256+(\tfrac{1}{5})^2[3(0-\tfrac{1}{5})^2+2(1-\tfrac{1}{5})^2]=0.288 }[/math]
2	17	F	5	[math]\displaystyle{ 0.288+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.320 }[/math]
1	17	S	4
2	19	S	3
3	20	F	3	[math]\displaystyle{ 0.320+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+2(0-\tfrac{1}{5})^2]=0.394 }[/math]
5	22	F	3	[math]\displaystyle{ 0.394+(\tfrac{1}{5})^2[2(0-\tfrac{1}{5})^2+4(1-\tfrac{1}{5})^2]=0.468 }[/math]
4	24	S	2
3	25	F	2	[math]\displaystyle{ 0.468+(\tfrac{1}{5})^2[(1-\tfrac{1}{5})^2+4(0-\tfrac{1}{5})^2]=0.593 }[/math]
5	25	F	2	[math]\displaystyle{ 0.580+(\tfrac{1}{5})^2[(0-\tfrac{1}{5})^2+4(1-\tfrac{1}{5})^2]=0.718 }[/math]
3	26	S	1
5	28	S	0

Using equation for the MCF bounds and [math]\displaystyle{ {{K}_{5}}=1.644 }[/math] for a 95% confidence level, the confidence bounds can be obtained as follows:

[math]\displaystyle{ \begin{matrix} ID & Months & State & MC{{F}_{i}} & Va{{r}_{i}} & MC{{F}_{{{L}_{i}}}} & MC{{F}_{{{U}_{i}}}} \\ \text{1} & \text{5} & \text{F} & \text{0}\text{.20} & \text{0}\text{.032} & 0.0459 & 0.8709 \\ \text{2} & \text{6} & \text{F} & \text{0}\text{.40} & \text{0}\text{.064} & 0.1413 & 1.1320 \\ \text{1} & \text{10} & \text{F} & \text{0}\text{.60} & \text{0}\text{.096} & 0.2566 & 1.4029 \\ \text{3} & \text{12} & \text{F} & \text{0}\text{.80} & \text{0}\text{.128} & 0.3834 & 1.6694 \\ \text{2} & \text{13} & \text{F} & \text{1}\text{.00} & \text{0}\text{.160} & 0.5179 & 1.9308 \\ \text{4} & \text{13} & \text{F} & \text{1}\text{.20} & \text{0}\text{.192} & 0.6582 & 2.1879 \\ \text{1} & \text{15} & \text{F} & \text{1}\text{.40} & \text{0}\text{.224} & 0.8028 & 2.4413 \\ \text{4} & \text{15} & \text{F} & \text{1}\text{.60} & \text{0}\text{.256} & 0.9511 & 2.6916 \\ \text{5} & \text{16} & \text{F} & \text{1}\text{.80} & \text{0}\text{.288} & 1.1023 & 2.9393 \\ \text{2} & \text{17} & \text{F} & \text{2}\text{.0} & \text{0}\text{.320} & 1.2560 & 3.1848 \\ \text{1} & \text{17} & \text{S} & {} & {} & {} & {} \\ \text{2} & \text{19} & \text{S} & {} & {} & {} & {} \\ \text{3} & \text{20} & \text{F} & \text{2}\text{.33} & \text{0}\text{.394} & 1.4990 & 3.6321 \\ \text{5} & \text{22} & \text{F} & \text{2}\text{.66} & \text{0}\text{.468} & 1.7486 & 4.0668 \\ \text{4} & \text{24} & \text{S} & {} & {} & {} & {} \\ \text{3} & \text{25} & \text{F} & \text{3}\text{.16} & \text{0}\text{.593} & 2.1226 & 4.7243 \\ \text{5} & \text{25} & \text{F} & \text{3}\text{.66} & \text{0}\text{.718} & 2.5071 & 5.3626 \\ \text{3} & \text{26} & \text{S} & {} & {} & {} & {} \\ \text{5} & \text{28} & \text{S} & {} & {} & {} & {} \\ \end{matrix} }[/math]

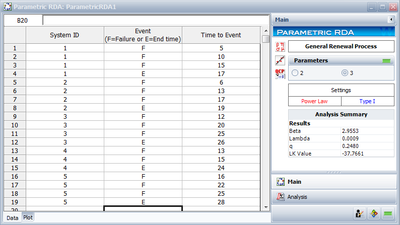
The analysis presented in Examples 1 and 2 can be obtained automatically in Weibull ++ using the Non-Parametric RDA Specialized Folio, as shown next.

Note: In the above Folio, the [math]\displaystyle{ F }[/math] refers to failures and [math]\displaystyle{ E }[/math] refers to suspensions (or censoring ages).

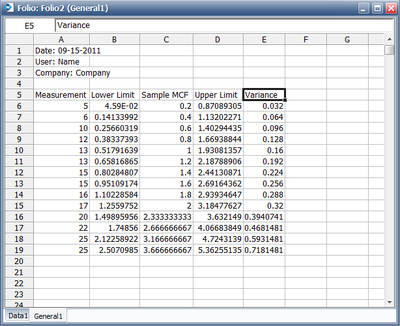
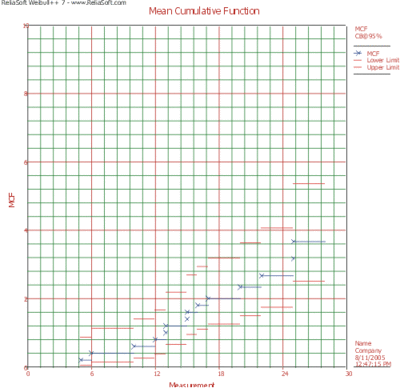
The results with calculated MCF values and upper and lower 95% confidence limits are shown next along with the graphical plot.