Template:Characteristics of the generalized gamma distribution

Characteristics of the Generalized Gamma Distribution

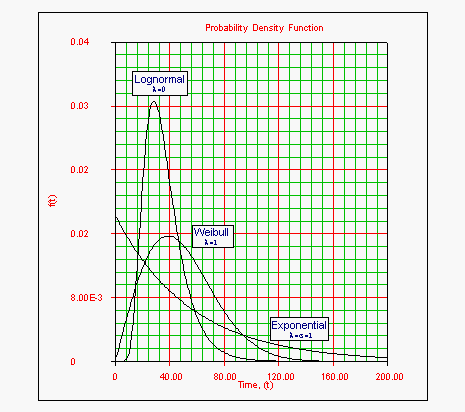
As mentioned previously, the generalized gamma distribution includes other distributions as special cases based on the values of the parameters.

• The Weibull distribution is a special case when [math]\displaystyle{ \lambda =1 }[/math] and:

[math]\displaystyle{ \begin{align} & \beta = \frac{1}{\sigma } \\ & \eta = & \ln (\mu ) \end{align} }[/math]

• In this case, the generalized distribution has the same behavior as the Weibull for [math]\displaystyle{ \sigma \gt 1, }[/math] [math]\displaystyle{ \sigma =1, }[/math] and [math]\displaystyle{ \sigma \lt 1 }[/math] ( [math]\displaystyle{ \beta \lt 1, }[/math] [math]\displaystyle{ \beta =1, }[/math] and [math]\displaystyle{ \beta \gt 1 }[/math] respectively).

• The exponential distribution is a special case when [math]\displaystyle{ \lambda =1 }[/math] and [math]\displaystyle{ \sigma =1 }[/math].

• The lognormal distribution is a special case when [math]\displaystyle{ \lambda =0 }[/math].

• The gamma distribution is a special case when [math]\displaystyle{ \lambda =\sigma }[/math].

By allowing [math]\displaystyle{ \lambda }[/math] to take negative values, the generalized gamma distribution can be further extended to include additional distributions as special cases. For example, the Fréchet distribution of maxima (also known as a reciprocal Weibull) is a special case when [math]\displaystyle{ \lambda =-1 }[/math].