Template:Example: Normal Distribution RRX

Normal Distribution RRX Example

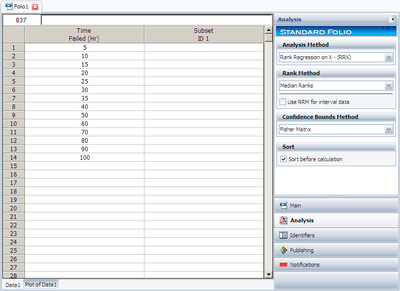
Using the data of Example 2 and assuming a normal distribution, estimate the parameters and determine the correlation coefficient, [math]\displaystyle{ \rho }[/math] , using rank regression on X.

Solution

Table 8.2 constructed in Example 2 applies to this example also. Using the values on this table, we get:

[math]\displaystyle{ \begin{align} \hat{b}= & \frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}}{{y}_{i}}-\tfrac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}}\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}}}{14}}{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,y_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}} \right)}^{2}}}{14}} \\ \widehat{b}= & \frac{365.2711-(630)(0)/14}{11.3646-{{(0)}^{2}}/14}=32.1411 \end{align} }[/math]

and:

[math]\displaystyle{ \hat{a}=\overline{x}-\hat{b}\overline{y}=\frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{t}_{i}}}{14}-\widehat{b}\frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}}}{14} }[/math]

or:

[math]\displaystyle{ \widehat{a}=\frac{630}{14}-(32.1411)\frac{(0)}{14}=45 }[/math]

Therefore:

[math]\displaystyle{ \widehat{\sigma }=\widehat{b}=32.1411 }[/math]

and:

[math]\displaystyle{ \widehat{\mu }=\widehat{a}=45\text{ hours} }[/math]

The correlation coefficient is obtained as:

[math]\displaystyle{ \widehat{\rho }=0.979 }[/math]

Note that the results for regression on X are not necessarily the same as the results for regression on Y. The only time when the two regressions are the same (i.e. will yield the same equation for a line) is when the data lie perfectly on a straight line. Using Weibull++ , Rank Regression on X (RRX) can be selected from the Analysis page.

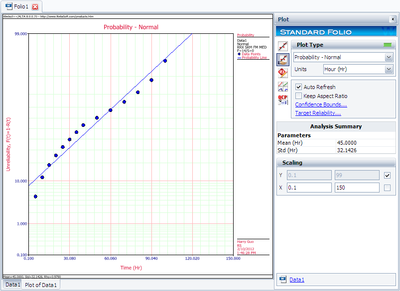
The plot of the solution for this example is shown next.

[math]\displaystyle{ }[/math]