Template:T-H Model

Temperature-Humidity Relationship

Introduction

The Temperature-Humidity (T-H) relationship, a variation of the Eyring relationship, has been proposed for predicting the life at use conditions when temperature and humidity are the accelerated stresses in a test. This combination model is given by:

$L(V,U)=A{e}^{\frac{\varphi }{V}+\frac{b}{U}}$

where:
• $\varphi$ is one of the three parameters to be determined.

• $b$ is the second of the three parameters to be determined (also known as the activation energy for humidity).

• $A$ is a constant and the third of the three parameters to be determined.

• $U$ is the relative humidity (decimal or percentage).

• $V$ is temperature (in absolute units ).

The T-H relationship can be linearized and plotted on a Life vs. Stress plot. The relationship is linearized by taking the natural logarithm of both sides in Eqn. (Temp-Hum), or:

$ln(L(V,U))=ln(A)+\frac{\varphi }{V}+\frac{b}{U}$

Since life is now a function of two stresses, a Life vs. Stress plot can only be obtained by keeping one of the two stresses constant and varying the other one. Doing so will yield a straight line as described by Eqn. (ln Temp-Hum), where the term for the stress which is kept at a fixed value becomes another constant (in addition to the $\ln (A)$ constant). In Figs. 1 and 2, data obtained from a temperature and humidity test were analyzed and plotted on Arrhenius paper. In Fig. 1, life is plotted versus temperature with relative humidity held at a fixed value. In Fig. 2, life is plotted versus relative humidity with temperature held at a fixed value.

Life vs. Temperature plot at a fixed relative humidity.

Life vs. Relative Humidity plot at a fixed temperature.

Note that the Life vs. Stress plots in both Figs. 1 and 2 are plotted on a log-reciprocal scale. Also note that the points shown in these plots represent the life characteristics at the test stress levels (the data set was fitted to a Weibull distribution, thus the points represent the scale parameter, $\eta )$ . For example, the points shown in Fig. 1 represent $\eta$ at each of the test temperature levels (two temperature levels were considered in this test).

A look at the Parameters $\varphi$ and $b$

Depending on which stress type is kept constant, it can be seen from Eqn. (ln Temp-Hum) that either the parameter $\varphi$ or the parameter $b$ is the slope of the resulting line. If, for example, the humidity is kept constant (Fig. 1) then $\varphi$ is the slope of the life line in a Life vs. Temperature plot. The steeper the slope, the greater the dependency of product life to the temperature. In other words, $\varphi$ is a measure of the effect that temperature has on the life, and $b$ is a measure of the effect that relative humidity has on the life. The larger the value of $\varphi ,$ the higher the dependency of the life on the temperature. Similarly, the larger the value of $b,$ the higher the dependency of the life on the humidity. For example, it can be seen by comparing Figs. 1 and 2 that, for this data set, temperature has a greater effect on the life than humidity.

T-H Data

When using the T-H relationship, the effect of both temperature and humidity on life is sought. For this reason, the test must be performed in a combination manner between the different stress levels of the two stress types. For example, assume that an accelerated test is to be performed at two temperature and two humidity levels. The two temperature levels were chosen to be 300K and 343K. The two humidity levels were chosen to be 0.6 and 0.8. It would be wrong to perform the test at (300K, 0.6) and (343K, 0.8). Doing so would not provide information about the temperature-humidity effects on life. This is because both stresses are increased at the same time and therefore it is unknown which stress is causing the acceleration on life. A possible combination that would provide information about temperature-humidity effects on life would be (300K, 0.6), (300K, 0.8) and (343K, 0.8). It is clear that by testing at (300K, 0.6) and (300K, 0.8) the effect of humidity on life can be determined (since temperature remained constant). Similarly the effects of temperature on life can be determined by testing at (300K, 0.8) and (343K, 0.8) since humidity remained constant.

Acceleration Factor

The acceleration factor for the T-H relationship is given by:

$A_F=\frac{L_{USE}}{L_{Accelerated}}=\frac{A{e}^{\frac{\varphi }{V_u}+\frac{b}{U_u}}}{A{e}^{\frac{\varphi }{V_A}+\frac{b}{U_A}}}=e^{\varphi (\frac{1}{V_u}-\frac{1}{V_A})+b(\frac{1}{U_u}-\frac{1}{U_A})}$

where:
• $L_{USE}$ is the life at use stress level.

• $L_{Accelerated}$ is the life at the accelerated stress level.

• $V_u$ is the use temperature level.

• $V_A$ is the accelerated temperature level.

• $U_A$ is the accelerated humidity level.

• $U_u$ is the use humidity level.

The acceleration Factor is plotted versus stress in the same manner used to create the Life vs. Stress plots. That is, one stress type is kept constant and the other is varied (see Figs. 3 and 4).

Acceleration Factor vs. Temperature at a fixed relative humidity.

Acceleration Factor vs. Humidity at a fixed temperature.

T-H Exponential

By setting $m=L(U,V)$ in Eqn. (Temp-Hum) the exponential $pdf$ becomes:

$f(t,V,U)=\frac{1}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}\cdot e^{-\frac{t}{A}\cdot e^{-(\frac{\varphi }{V}+\frac{b}{U})}}$

T-H Exponential Statistical Properties Summary

Mean or MTTF

The mean, $\bar{T},$ or Mean Time To Failure (MTTF) for the T-H exponential model is given by:

$\bar{T}=\underset{0}{\overset{\mathrm{\infty }}{}}t\cdot f(t,V,U)dt$

Substituting Eqn. (t-h exp pdf) yields:

$\begin{array}{rlr}& \bar{T}=& \underset{0}{\overset{\mathrm{\infty }}{}}t\cdot \frac{1}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}{e}^{-\frac{t}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}}dt\\ & =& A{e}^{\frac{\varphi }{V}+\frac{b}{U}}\end{array}$

Median

The median, $\breve{T},$ for the T-H exponential model is given by:

$\breve{T}=0.693\cdot A{e}^{\frac{\varphi }{V}+\frac{b}{U}}$

Mode

The mode, $\tilde{T},$ for the T-H exponential model is given by:

$\tilde{T}=0$

Standard Deviation

The standard deviation, ${\sigma }_T$ , for the T-H exponential model is given by:

${\sigma }_T=A{e}^{\frac{\varphi }{V}+\frac{b}{U}}$

T-H Exponential Reliability Function

The T-H exponential reliability function is given by:

$R(T,V,U)=e^{-\frac{T}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}}$

This function is the complement of the T-H exponential cumulative distribution function or:

$R(T,V,U)=1-Q(T,V,U)=1-\underset{0}{\overset{T}{}}f(T)dT$

and:

$R(T,V,U)=1-\underset{0}{\overset{T}{}}\frac{1}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}{e}^{-\frac{T}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}}dT=e^{-\frac{T}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}}$

Conditional Reliability

The conditional reliability function for the T-H exponential model is given by:

$R(T,t,V,U)=\frac{R(T+t,V,U)}{R(T,V,U)}=\frac{e^{-\lambda (T+t)}}{e^{-\lambda T}}=e^{-\frac{t}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}}$

Reliable Life

For the T-H exponential model, the reliable life, or the mission duration for a desired reliability goal, $t_R,$ is given by:

$R(t_R,V,U)=e^{-\frac{t_R}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}}$

$\ln [R(t_R,V,U)]=-\frac{t_R}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}$

or:

$t_R=-A{e}^{\frac{\varphi }{V}+\frac{b}{U}}\ln [R(t_R,V,U)]$

Parameter Estimation

Maximum Likelihood Estimation Method

Substituting the T-H model into the exponential log-likelihood equation yields:

$\begin{array}{rlr}& \ln (L)=& \mathrm{\Lambda }=\underset{i=1}{\sum ^{F_e}}{N}_i\ln [\frac{1}{A}{e}^{-(\frac{\varphi }{V_i}+\frac{b}{U_i})}\cdot e^{-\frac{T_i}{A}\cdot e^{-(\frac{\varphi }{V_i}+\frac{b}{U_i})}}]\\ & & -\underset{i=1}{\sum ^S}{N}_i^{\prime }\frac{T_i^{\prime }}{A}{e}^{-(\frac{\varphi }{V_i}+\frac{b}{U_i})}+\stackrel{FI}{\sum ^{}_{}_{i=1}}{N}_i^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }]\end{array}$

where:

$R_{Li}^{\prime \prime }=e^{-\frac{T_{Li}^{\prime \prime }}{A}{e}^{-(\frac{\varphi }{V_i}+\frac{b}{U_i^{\prime \prime }})}}$

$R_{Ri}^{\prime \prime }=e^{-\frac{T_{Ri}^{\prime \prime }}{A}{e}^{-(\frac{\varphi }{V_i}+\frac{b}{U_i^{\prime \prime }})}}$

and:
• $F_e$ is the number of groups of exact times-to-failure data points.
• $N_i$ is the number of times-to-failure data points in the $i^{th}$ time-to-failure data group.
• $A$ is the T-H parameter (unknown, the first of three parameters to be estimated).
• $\varphi$ is the second T-H parameter (unknown, the second of three parameters to be estimated).
• $b$ is the third T-H parameter (unknown, the third of three parameters to be estimated).
• $V_i$ is the temperature level of the $i^{th}$ group.
• $U_i$ is the relative humidity level of the $i^{th}$ group.
• $T_i$ is the exact failure time of the $i^{th}$ group.
• $S$ is the number of groups of suspension data points.
• .. is the number of suspensions in the $i^{th}$ group of suspension data points.
• $T_i^{\prime }$ is the running time of the $i^{th}$ suspension data group.
• $FI$ is the number of interval data groups.
• $N_i^{\prime \prime }$ is the number of intervals in the $i^{th}$ group of data intervals.
• $T_{Li}^{\prime \prime }$ is the beginning of the $i^{th}$ interval.
• $T_{Ri}^{\prime \prime }$ is the ending of the $i^{th}$ interval.

The solution (parameter estimates) will be found by solving for the parameters $A,$ $\varphi$ and $b$ so that $\frac{\partial \mathrm{\Lambda }}{\partial A}=0,$ $\frac{\partial \mathrm{\Lambda }}{\partial \varphi }=0$ and $\frac{\partial \mathrm{\Lambda }}{\partial b}=0$ .

T-H Weibull

By setting $\eta =L(U,V)$ as given in Eqn. (Temp-Hum), the T--H Weibull model's $pdf$ is given by: ..

T-H Weibull Statistical Properties Summary

Mean or MTTF

The mean, $\bar{T}$ (also called $MTTF$ ), of the T-H Weibull model is given by:

$\bar{T}=A{e}^{\frac{\varphi }{V}+\frac{b}{U}}\cdot \mathrm{\Gamma }(\frac{1}{\beta }+1)$

where $\mathrm{\Gamma }(\frac{1}{\beta }+1)$ is the gamma function evaluated at the value of $(\frac{1}{\beta }+1)$ .

Median

The median, $\breve{T},$ of the T-H Weibull model is given by:

$\breve{T}=A{e}^{\frac{\varphi }{V}+\frac{b}{U}}{(\ln 2)}^{\frac{1}{\beta }}$

Mode

The mode, $\tilde{T},$ of the T-H Weibull model is given by:

$\tilde{T}=A{e}^{\frac{\varphi }{V}+\frac{b}{U}}{(1-\frac{1}{\beta })}^{\frac{1}{\beta }}$

Standard Deviation

The standard deviation, ${\sigma }_T,$ of the T-H Weibull model is given by:

${\sigma }_T=A{e}^{\frac{\varphi }{V}+\frac{b}{U}}\cdot \sqrt{\mathrm{\Gamma }(\frac{2}{\beta }+1)-{\left(\mathrm{\Gamma }(\frac{1}{\beta }+1)\right)}^2}$

T-H Weibull Reliability Function

The T-H Weibull reliability function is given by:

$R(T,V,U)=e^{-{\left(\frac{T}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}\right)}^{\beta }}$

Conditional Reliability Function

The T-H Weibull conditional reliability function at a specified stress level is given by:

$R(T,t,V,U)=\frac{R(T+t,V,U)}{R(T,V,U)}=\frac{e^{-{\left(\frac{T+t}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}\right)}^{\beta }}}{e^{-{\left(\frac{T}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}\right)}^{\beta }}}$

or:

$R(T,t,V,U)=e^{-[{\left(\frac{T+t}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}\right)}^{\beta }-{\left(\frac{T}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}\right)}^{\beta }]}$

Reliable Life

For the T-H Weibull model, the reliable life, $t_R$ , of a unit for a specified reliability and starting the mission at age zero is given by:

$t_R=A{e}^{\frac{\varphi }{V}+\frac{b}{U}}{\{-\ln \left[R(T_R,V,U)\right]\}}^{\frac{1}{\beta }}$

T-H Weibull Failure Rate Function

The T-H Weibull failure rate function, $\lambda (T,V,U)$ , is given by:

$\lambda (T,V,U)=\frac{f(T,V,U)}{R(T,V,U)}=\frac{\beta }{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}{\left(\frac{T}{A}{e}^{-(\frac{\varphi }{V}+\frac{b}{U})}\right)}^{\beta -1}$

Parameter Estimation

Maximum Likelihood Estimation Method

Substituting the T-H model into the Weibull log-likelihood function yields:

$\begin{array}{rlr}& \ln (L)=& \mathrm{\Lambda }=\underset{i=1}{\sum ^{F_e}}{N}_i\ln \left[\frac{\beta }{A}{e}^{-(\frac{\varphi }{V_i}+\frac{b}{U_i})}{\left(\frac{T_i}{A}{e}^{-(\frac{\varphi }{V_i}+\frac{b}{U_i})}\right)}^{\beta -1}{e}^{-{\left(\frac{T_i}{A}{e}^{-(\frac{\varphi }{V_i}+\frac{b}{U_i})}\right)}^{\beta }}\right]\\ & & -\underset{i=1}{\sum ^S}{N}_i^{\prime }{\left(\frac{T_i^{\prime }}{A}{e}^{-(\frac{\varphi }{V_i}+\frac{b}{U_i})}\right)}^{\beta }+\stackrel{FI}{\sum ^{}_{}_{i=1}}{N}_i^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }]\end{array}$

where:

$R_{Li}^{\prime \prime }=e^{-{\left(\frac{T_{Li}^{\prime \prime }}{A}{e}^{-(\frac{\varphi }{V_i}+\frac{b}{U_i^{\prime \prime }})}\right)}^{\beta }}$

$R_{Ri}^{\prime \prime }=e^{-{\left(\frac{T_{Ri}^{\prime \prime }}{A}{e}^{-(\frac{\varphi }{V_i}+\frac{b}{U_i^{\prime \prime }})}\right)}^{\beta }}$

and:
• $F_e$ is the number of groups of exact times-to-failure data points.
• $N_i$ is the number of times-to-failure data points in the $i^{th}$ time-to-failure data group.
• $\beta$ is the Weibull shape parameter (unknown, the first of four parameters to be estimated).
• .. is the T-H parameter (unknown, the second of four parameters to be estimated).
• $\varphi$ is the second T-H parameter (unknown, the third of four parameters to be estimated).
• $b$ is the third T-H parameter (unknown, the fourth of four parameters to be estimated).
• $V_i$ is the temperature level of the $i^{th}$ group.
• $U_i$ is the relative humidity level of the $i^{th}$ group.
• $T_i$ is the exact failure time of the $i^{th}$ group.
• $S$ is the number of groups of suspension data points.
• $N_i^{\prime }$ is the number of suspensions in the $i^{th}$ group of suspension data points.
• $T_i^{\prime }$ is the running time of the $i^{th}$ suspension data group.
• $FI$ is the number of interval data groups.
• $N_i^{\prime \prime }$ is the number of intervals in the $i^{th}$ group of data intervals.
• $T_{Li}^{\prime \prime }$ is the beginning of the interval.
• $T_{Ri}^{\prime \prime }$ is the ending of the $i^{th}$ interval.
The solution (parameter estimates) will be found by solving for the parameters $A,$ $\varphi ,$ $b$ and $\beta$ so that $\frac{\partial \mathrm{\Lambda }}{\partial \beta }=0,$ $\frac{\partial \mathrm{\Lambda }}{\partial A}=0,$ $\frac{\partial \mathrm{\Lambda }}{\partial \varphi }=0$ and $\frac{\partial \mathrm{\Lambda }}{\partial b}=0$ .

Example

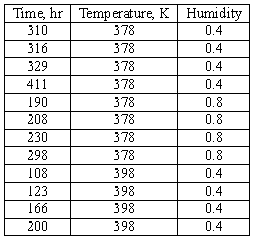
The following data were collected after testing twelve electronic devices at different temperature and humidity conditions:

Using ALTA, the following results were obtained:

$\begin{array}{rlr}& \hat{\beta }=& 5.87439512\\ & & \\ & \hat{A}=& 0.0000597\\ & & \\ & \hat{b}=& 0.2805985\\ & & \\ & \hat{\varphi }=& 5630.329851\end{array}$

A probability plot for the entered data is shown next.

Probability plots at the tested combinations.

Note that three lines are plotted because there are three combinations of stresses, namely, (398K, 0.4), (378K, 0.8) and (378K, 0.4).

Given the use stress levels, time estimates can be obtained for specified probability. A Life vs. Stress plot can be obtained if one of the stresses is kept constant. For example, the following picture is a Life vs. Humidity plot at a constant temperature of 338K.

Life vs. Humidity plot with temperature fixed at 338K.

T-H Lognormal

The $pdf$ of the lognormal distribution is given by:

$f(T)=\frac{1}{T{\sigma }_{T^{\prime }}\sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{T^{\prime }-\overline{T^{\prime }}}{{\sigma }_{T^{\prime }}}\right)}^2}$

where:

$T^{\prime }=\ln (T)$

$T=\text{times-to-failure}$

and:
• $\overline{T^{\prime }}=$ mean of the natural logarithms of the times-to-failure. • ${\sigma }_{T^{\prime }}=$ standard deviation of the natural logarithms of the times-to-failure.
The median of the lognormal distribution is given by:

$\breve{T}=e^{{\bar{T}}^{\prime }}$

The T-H lognormal model $pdf$ can be obtained first by setting $\breve{T}=L(V,U)$ in Eqn. (Temp-Hum).
Therefore:

$\breve{T}=L(V,U)=A{e}^{\frac{\varphi }{V}+\frac{b}{U}}$

or:

$e^{{\bar{T}}^{\prime }}=A{e}^{\frac{\varphi }{V}+\frac{b}{U}}$

Thus:

${\bar{T}}^{\prime }=\ln (A)+\frac{\varphi }{V}+\frac{b}{U}.$

Substituting Eqn. (TH-logn-mean) into Eqn. (TH-logn-pdf) yields the T-H lognormal model $pdf$ or:

$f(T,V,U)=\frac{1}{T{\sigma }_{T^{\prime }}\sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{T^{\prime }-\ln (A)-\frac{\varphi }{V}-\frac{b}{U}}{{\sigma }_{T^{\prime }}}\right)}^2}$

T-H Lognormal Statistical Properties Summary

The Mean

• The mean life of the T-H lognormal model (mean of the times-to-failure), $\overline{T}$ , is given by:

$\begin{array}{rlr}& \overline{T}=& e^{\overline{T^{\prime }}+\frac{1}{2}{\sigma }_{T^{\prime }}^2}\\ & =& e^{\ln (A)+\frac{\varphi }{V}+\frac{b}{U}+\frac{1}{2}{\sigma }_{T^{\prime }}^2}\end{array}$

• The mean of the natural logarithms of the times-to-failure, ${\overline{T}}^{{}^{\prime }}$ , in terms of $\overline{T}$ and ${\sigma }_T$ is given by:

${\overline{T}}^{\prime }=\ln \left(\overline{T}\right)-\frac{1}{2}\ln (\frac{{\sigma }_T^2}{{\overline{T}}^2}+1)$

The Standard Deviation

• The standard deviation of the T-H lognormal model (standard deviation of the times-to-failure), ${\sigma }_T$ , is given by:

$\begin{array}{rlr}& {\sigma }_T=& \sqrt{\left(e^{2\overline{T^{\prime }}+{\sigma }_{T^{\prime }}^2}\right)(e^{{\sigma }_{T^{\prime }}^2}-1)}\\ & =& \sqrt{\left(e^{2(\ln (A)+\frac{\varphi }{V}+\frac{b}{U})+{\sigma }_{T^{\prime }}^2}\right)(e^{{\sigma }_{T^{\prime }}^2}-1)}\end{array}$

• The standard deviation of the natural logarithms of the times-to-failure, ${\sigma }_{T^{\prime }}$ , in terms of $\overline{T}$ and ${\sigma }_T$ is given by:

${\sigma }_{T^{\prime }}=\sqrt{\ln (\frac{{\sigma }_T^2}{{\overline{T}}^2}+1)}$

The Mode

• The mode of the T-H lognormal model is given by:

$\begin{array}{rlr}& \tilde{T}=& e^{{\bar{T}}^{\prime }-{\sigma }_{T^{\prime }}^2}\\ & =& e^{\ln (A)+\frac{\varphi }{V}+\frac{b}{U}-{\sigma }_{T^{\prime }}^2}\end{array}$

T-H Lognormal Reliability

The reliability for a mission of time $T$ , starting at age 0, for the T-H lognormal model is determined by:

$R(T,V,U)=\underset{T}{\overset{\mathrm{\infty }}{}}f(t,V,U)dt$

or:

$R(T,V,U)=\underset{T^{{}^{\prime }}}{\overset{\mathrm{\infty }}{}}\frac{1}{{\sigma }_{T^{\prime }}\sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{t-\ln (A)-\frac{\varphi }{V}-\frac{b}{U}}{{\sigma }_{T^{\prime }}}\right)}^2}dt$

There is no closed form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability, we will not discuss manual solution methods.

Reliable Life

For the T-H lognormal model, the reliable life, or the mission duration for a desired reliability goal, $t_R,$ is estimated by first solving the reliability equation with respect to time, as follows:

$T_R^{\prime }=\ln (A)+\frac{\varphi }{V}+\frac{b}{U}+z\cdot {\sigma }_{T^{\prime }}$

where:

$z={\mathrm{\Phi }}^{-1}\left[F(T_R^{\prime },V,U)\right]$

and:

$\mathrm{\Phi }(z)=\frac{1}{\sqrt{2\pi }}\underset{-\mathrm{\infty }}{\overset{z(T^{\prime },V,U)}{}}{e}^{-\frac{t^2}{2}}dt$

Since $T^{\prime }=\ln (T),$ the reliable life, $t_{R,}$ is given by:

$t_R=e^{T_R^{\prime }}$

T-H Lognormal Failure Rate

The lognormal failure rate is given by:

$\lambda (T,V,U)=\frac{f(T,V,U)}{R(T,V,U)}=\frac{\frac{1}{T{\sigma }_{T^{\prime }}\sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{T^{\prime }-\ln (A)-\frac{\varphi }{V}-\frac{b}{U}}{{\sigma }_{T^{\prime }}}\right)}^2}}{{}_{T^{\prime }}^{\mathrm{\infty }}\frac{1}{{\sigma }_{T^{\prime }}\sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{T^{\prime }-\ln (A)-\frac{\varphi }{V}-\frac{b}{U}}{{\sigma }_{T^{\prime }}}\right)}^2}dt}$

Parameter Estimation

Maximum Likelihood Estimation Method

The complete T-H lognormal log-likelihood function is:

$\begin{array}{rlr}& \ln (L)=& \mathrm{\Lambda }=\underset{i=1}{\sum ^{F_e}}{N}_i\ln \left[\frac{1}{{\sigma }_{T^{\prime }}{T}_i}{\varphi }_{pdf}\left(\frac{\ln \left(T_i\right)-\ln (A)-\frac{\varphi }{V_i}-\frac{b}{U_i}}{{\sigma }_{T^{\prime }}}\right)\right]\\ & & +\underset{i=1}{\sum ^S}{N}_i^{\prime }\ln [1-\mathrm{\Phi }\left(\frac{\ln \left(T_i^{\prime }\right)-\ln (A)-\frac{\varphi }{V_i}-\frac{b}{U_i}}{{\sigma }_{T^{\prime }}}\right)]\\ & & +\stackrel{FI}{\sum ^{}_{}_{i=1}}{N}_i^{\prime \prime }\ln [\mathrm{\Phi }(z_{Ri}^{\prime \prime })-\mathrm{\Phi }(z_{Li}^{\prime \prime })]\end{array}$

where:

$z_{Li}^{\prime \prime }=\frac{\ln T_{Li}^{\prime \prime }-\ln A-\frac{\varphi }{V_i}-\frac{b}{U_i^{\prime \prime }}}{{\sigma }_T^{\prime }}$

$z_{Ri}^{\prime \prime }=\frac{\ln T_{Ri}^{\prime \prime }-\ln A-\frac{\varphi }{V_i}-\frac{b}{U_i^{\prime \prime }}}{{\sigma }_T^{\prime }}$

${\varphi }_{pdf}\left(x\right)=\frac{1}{\sqrt{2\pi }}\cdot e^{-\frac{1}{2}{\left(x\right)}^2}$

$\mathrm{\Phi }(x)=\frac{1}{\sqrt{2\pi }}\underset{-\mathrm{\infty }}{\overset{x}{}}{e}^{-\frac{t^2}{2}}dt$

and:
• $F_e$ is the number of groups of exact times-to-failure data points.
• $N_i$ is the number of times-to-failure data points in the $i^{th}$ time-to-failure data group.
• ${\sigma }_{T^{\prime }}$ is the standard deviation of the natural logarithm of the times-to-failure (unknown, the first of four parameters to be estimated).
• $A$ is the first T-H parameter (unknown, the second of four parameters to be estimated).
• $\varphi$ is the second T-H parameter (unknown, the third of four parameters to be estimated).
• $b$ is the third T-H parameter (unknown, the fourth of four parameters to be estimated).
• $V_i$ is the stress level for the first stress type (i.e. temperature) of the $i^{th}$ group.
• $U_i$ is the stress level for the second stress type (i.e. relative humidity) of the $i^{th}$ group.
• $T_i$ is the exact failure time of the $i^{th}$ group.
• $S$ is the number of groups of suspension data points.
• $N_i^{\prime }$ is the number of suspensions in the $i^{th}$ group of suspension data points.
• $T_i^{\prime }$ is the running time of the $i^{th}$ suspension data group.
• $FI$ is the number of interval data groups.
• $N_i^{\prime \prime }$ is the number of intervals in the $i^{th}$ group of data intervals.
• $T_{Li}^{\prime \prime }$ is the beginning of the $i^{th}$ interval. • $T_{Ri}^{\prime \prime }$ is the ending of the $i^{th}$ interval.
•
The solution (parameter estimates) will be found by solving for ${\hat{\sigma }}_{T^{\prime }},$ $\hat{A},$ $\hat{\varphi },$ $\hat{b}$ so that $\frac{\partial \mathrm{\Lambda }}{\partial {\sigma }_{T^{\prime }}}=0,$ $\frac{\partial \mathrm{\Lambda }}{\partial A}=0,$ $\frac{\partial \mathrm{\Lambda }}{\partial \varphi }=0$ and $\frac{\partial \mathrm{\Lambda }}{\partial b}=0$ .