Template:Alta exponential distribution

The Exponential Distribution

The exponential distribution is a very commonly used distribution in reliability engineering. Due to its simplicity, it has been widely employed even in cases to which it does not apply. The exponential distribution is used to describe units that have a constant failure rate. The single-parameter exponential [math]\displaystyle{ pdf }[/math] is given by:

[math]\displaystyle{ \begin{align} & f(T)= & \lambda {{e}^{-\lambda T}}=\frac{1}{m}{{e}^{-\tfrac{1}{m}T}} \\ & T\ge & 0,\lambda \gt 0,m\gt 0 \end{align} }[/math]

where:

• [math]\displaystyle{ \lambda = }[/math] constant failure rate, in failures per unit of measurement, e.g. failures per hour, per cycle, etc.

• [math]\displaystyle{ \lambda =\tfrac{1}{m}. }[/math]

• [math]\displaystyle{ m= }[/math] mean time between failures, or to a failure.

• [math]\displaystyle{ T= }[/math] operating time, life, or age, in hours, cycles, miles, actuations, etc.

This distribution requires the estimation of only one parameter, [math]\displaystyle{ \lambda }[/math] , for its application.

Statistical Properties Summary

The Mean or MTTF

The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) of the 1-parameter exponential distribution is given by:

[math]\displaystyle{ \begin{align} & \overline{T}= & \mathop{}_{0}^{\infty }t\cdot f(t)dt=\mathop{}_{0}^{\infty }t\cdot \lambda \cdot {{e}^{-\lambda t}}dt \\ & = & \frac{1}{\lambda } \end{align} }[/math]

The Median

The median, [math]\displaystyle{ \breve{T} }[/math], of the 1-parameter exponential distribution is given by:

[math]\displaystyle{ \breve{T}=\frac{1}{\lambda }0.693 }[/math]

The Mode

The mode, [math]\displaystyle{ \tilde{T}, }[/math] of the 1-parameter exponential distribution is given by:

[math]\displaystyle{ \tilde{T}=0 }[/math]

The Standard Deviation

The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math] , of the 1-parameter exponential distribution is given by:

[math]\displaystyle{ {{\sigma }_{T}}=\frac{1}{\lambda }=m }[/math]

The Reliability Function

The 1-parameter exponential reliability function is given by:

[math]\displaystyle{ R(T)={{e}^{-\lambda T}}={{e}^{-\tfrac{T}{m}}} }[/math]

This function is the complement of the exponential cumulative distribution function or:

[math]\displaystyle{ R(T)=1-Q(T)=1-\mathop{}_{0}^{T}f(T)dT }[/math]

and:

[math]\displaystyle{ R(T)=1-\mathop{}_{0}^{T}\lambda {{e}^{-\lambda T}}dT={{e}^{-\lambda T}} }[/math]

Conditional Reliability

The conditional reliability function for the 1-parameter exponential distribution is given by:

[math]\displaystyle{ R(T,t)=\frac{R(T+t)}{R(T)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\lambda t}} }[/math]

which says that the reliability for a mission of [math]\displaystyle{ t }[/math] duration undertaken after the component or equipment has already accumulated [math]\displaystyle{ T }[/math] hours of operation from age zero is only a function of the mission duration, and not a function of the age at the beginning of the mission. This is referred to as the ``memoryless property.

Reliable Life

The reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}} }[/math] , for the 1-parameter exponential distribution is given by:

[math]\displaystyle{ \begin{align} & R({{t}_{R}})= & {{e}^{-\lambda {{t}_{R}}}} \\ & & \\ & \ln [R({{t}_{R}})]= & -\lambda {{t}_{R}} \end{align} }[/math]

or:

[math]\displaystyle{ {{t}_{R}}=-\frac{\ln [R({{t}_{R}})]}{\lambda } }[/math]

Failure Rate Function

The exponential failure rate function is given by:

[math]\displaystyle{ \lambda (T)=\frac{f(T)}{R(T)}=\frac{\lambda {{e}^{-\lambda (T)}}}{{{e}^{-\lambda (T)}}}=\lambda =\text{Constant} }[/math]

Characteristics

The characteristics of the 1-parameter exponential distribution can be exemplified by examining its parameter, lambda, [math]\displaystyle{ \lambda , }[/math] and the effect lambda has on the [math]\displaystyle{ pdf }[/math] , reliability and failure rate functions.

Effects of [math]\displaystyle{ \lambda }[/math] on the pdf

Pdf plot of the exponential distribution.

• The scale parameter is [math]\displaystyle{ \tfrac{1}{\lambda } }[/math] .

• As [math]\displaystyle{ \lambda }[/math] is decreased in value, the distribution is stretched out to the right, and as [math]\displaystyle{ \lambda }[/math] is increased, the distribution is pushed toward the origin.

• This distribution has no shape parameter as it has only one shape, i.e. the exponential. The only parameter it has is the failure rate, [math]\displaystyle{ \lambda }[/math] .

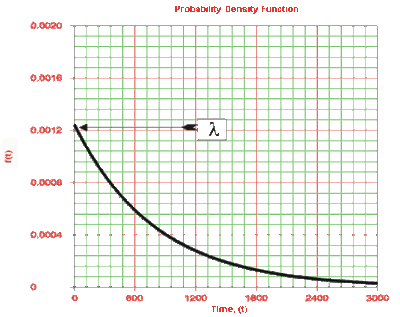
• The distribution starts at [math]\displaystyle{ T=0 }[/math] at the level of [math]\displaystyle{ f(T=0)=\lambda }[/math] and decreases thereafter exponentially and monotonically as [math]\displaystyle{ T }[/math] increases, and is convex.

• As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ f(T)\to 0 }[/math].

• This [math]\displaystyle{ pdf }[/math] can be thought of as a special case of the Weibull [math]\displaystyle{ pdf }[/math] with [math]\displaystyle{ \beta =1 }[/math] .

Reliability plot of the exponential distribution.

Effects of [math]\displaystyle{ \lambda }[/math] on the Reliability Function

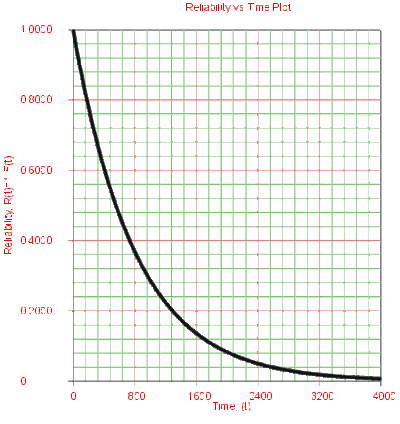
• The 1-parameter exponential reliability function starts at the value of 1 at [math]\displaystyle{ T=0 }[/math] . It decreases thereafter monotonically and is convex.

• As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ R(T\to \infty )\to 0 }[/math].

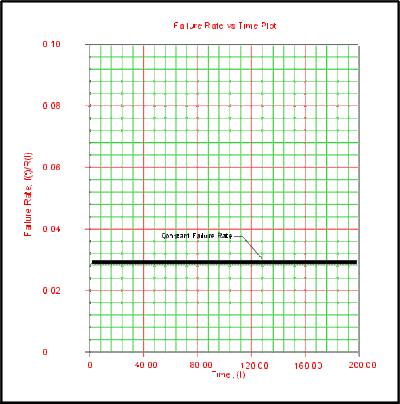
Effects of [math]\displaystyle{ \lambda }[/math] on the Failure Rate Function

The failure rate function for the exponential distribution is constant and it is equal to the parameter [math]\displaystyle{ \lambda }[/math] .

Failure Rate plot of the exponential distribution.