Template:Confidence bounds logistic rga
Confidence Bounds
Least squares is used to estimate the parameters of the following Logistic model.
- [math]\displaystyle{ \ln (\frac{1}{{{{\hat{R}}}_{i}}}-1)=\ln (b)-k{{T}_{i}} }[/math]
Thus the confidence bounds on the parameters are given by:
- [math]\displaystyle{ b=\hat{b}{{e}^{{{t}_{n-2,\alpha /2}}SE(\ln \hat{b})}} }[/math]
- where:
- [math]\displaystyle{ SE(\ln \hat{b})=\sigma \cdot \sqrt{\frac{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{({{T}_{i}})}^{2}}}{n\cdot {{S}_{xx}}}},\ \ \ {{S}_{xx}}=\left[ \underset{i=1}{\overset{n}{\mathop \sum }}\,{{({{T}_{i}})}^{2}} \right]-\frac{1}{n}{{\left( \underset{i=1}{\overset{n}{\mathop \sum }}\,{{T}_{i}} \right)}^{2}} }[/math]
- [math]\displaystyle{ \sigma =\sqrt{SSE/(n-2)} }[/math]
- and:
- [math]\displaystyle{ k=\hat{k}\pm {{t}_{n-2,\alpha /2}}SE(\hat{k}) }[/math]
- where:
- [math]\displaystyle{ SE(\hat{k})=\frac{\sigma }{\sqrt{{{S}_{xx}}}},\ \ {{S}_{xx}}=\left[ \underset{i=1}{\overset{n}{\mathop \sum }}\,{{({{T}_{i}})}^{2}} \right]-\frac{1}{n}{{\left( \underset{i=1}{\overset{n}{\mathop \sum }}\,{{T}_{i}} \right)}^{2}} }[/math]
Since the reliability is always between 0 and 1, the logit transformation is used to obtain the confidence bounds on reliability.
- [math]\displaystyle{ CB=\frac{{{{\hat{R}}}_{i}}}{{{{\hat{R}}}_{i}}+(1-{{{\hat{R}}}_{i}}){{e}^{\pm {{z}_{\alpha }}{{{\hat{\sigma }}}_{R}}/\left[ {{{\hat{R}}}_{i}}(1-{{{\hat{R}}}_{i}}) \right]}}} }[/math]
Example 4
For the data given for Example 1 in Table 8.1, calculate the 2-sided 90% confidence bounds under the Logistic model for the following:
- 1) The parameters [math]\displaystyle{ b }[/math] and [math]\displaystyle{ k }[/math] .
- 2) Reliability at month 5.
Solution
- 1) The values of [math]\displaystyle{ \widehat{b} }[/math] and [math]\displaystyle{ \widehat{k} }[/math] estimated from the least squares analysis in Example 1:
- [math]\displaystyle{ \begin{align} & \widehat{b}= & 3.3991 \\ & \widehat{\alpha }= & 0.7398 \end{align} }[/math]
Thus the 2-sided 90% confidence bounds on parameter [math]\displaystyle{ b }[/math] using Eqn. (LogCBb) are:
- [math]\displaystyle{ \begin{align} & {{b}_{lower}}= & 2.5547 \\ & {{b}_{upper}}= & 4.5225 \end{align} }[/math]
The 2-sided 90% confidence bounds on parameter [math]\displaystyle{ k }[/math] using Eqn. (logCBk) are:
- [math]\displaystyle{ \begin{align} & {{k}_{lower}}= & 0.6798 \\ & {{k}_{upper}}= & 0.7997 \end{align} }[/math]
- 2) First calculate the reliability estimation at month 5:
- [math]\displaystyle{ \begin{align} & {{R}_{5}}= & \frac{1}{1+b{{e}^{-5k}}} \\ & = & 0.9224 \end{align} }[/math]
Thus the 2-sided 90% confidence bounds on reliability at month 5 using Eqn. (LogCR) are:
- [math]\displaystyle{ \begin{align} & {{[{{R}_{5}}]}_{lower}}= & 0.8493 \\ & {{[{{R}_{5}}]}_{upper}}= & 0.9955 \end{align} }[/math]
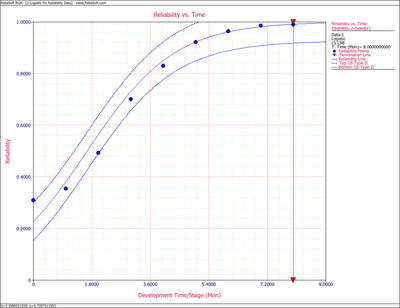
Figure Logig86 shows a graph of the reliability plotted with 2-sided 90% confidence bounds.