Template:Modified gompertz model

Modified Gompertz Model

Sometimes reliability growth data with an S-shaped trend cannot be described accurately by the Gompertz or Logistic (Chapter 8) curves. Since these two models have fixed values of reliability at the inflection points, only a few reliability growth data sets following an S-shaped reliability growth curve can be fitted to them. A modification of the Gompertz curve, which overcomes this shortcoming, is given next [5].
If we apply a shift in the vertical coordinate, then the Gompertz model is defined by:

[math]\displaystyle{ R=d+a{{b}^{{{c}^{T}}}} }[/math]

where:

[math]\displaystyle{ 0\lt a+d\le 1 }[/math]

[math]\displaystyle{ 0\lt b\lt 1,0\lt c\lt 1,\text{and}T\ge 0 }[/math]

[math]\displaystyle{ R }[/math] = system's reliability at development time [math]\displaystyle{ T }[/math] or at launch number [math]\displaystyle{ T }[/math], or stage number [math]\displaystyle{ T }[/math].

[math]\displaystyle{ d }[/math] = shift parameter.

[math]\displaystyle{ d+a }[/math] = upper limit that the reliability approaches asymptotically as [math]\displaystyle{ T\to\infty }[/math]

[math]\displaystyle{ d+ab }[/math] = initial reliability at [math]\displaystyle{ T=0 }[/math]

[math]\displaystyle{ c }[/math] = growth pattern indicator(small values of [math]\displaystyle{ c }[/math] indicate rapid early reliability growth and large values of [math]\displaystyle{ c }[/math] indicate slow reliability growth).

The Modified Gompertz model is more flexible than the original, especially when fitting growth data with S-shaped trends.

Parameter Estimation

To implement the Modified Gompertz growth model, initial values of the parameters [math]\displaystyle{ a }[/math] , [math]\displaystyle{ b }[/math] , [math]\displaystyle{ c }[/math] and [math]\displaystyle{ d }[/math] must be determined. When analyzing reliability data in RGA, you have the option to enter the reliability values in percent or in decimal format. However, [math]\displaystyle{ a }[/math] and [math]\displaystyle{ d }[/math] will always be returned in decimal format and not in percent. The estimated parameters in RGA are unitless. Given that [math]\displaystyle{ R=d+a{{b}^{{{c}^{T}}}} }[/math] and [math]\displaystyle{ \ln (R-d)=\ln (a)+{{c}^{T}}\ln (b) }[/math] , it follows that [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] and [math]\displaystyle{ {{S}_{3}} }[/math] , as defined in the derivation of the Standard Gompertz model, can be expressed as functions of [math]\displaystyle{ d }[/math] .

[math]\displaystyle{ \begin{align} & {{S}_{1}}(d)= & \underset{i=0}{\overset{n-1}{\mathop \sum }}\,\ln ({{R}_{i}}-d)=n\ln (a)+\ln (b)\underset{i=0}{\overset{n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \\ & {{S}_{2}}(d)= & \underset{i=n}{\overset{2n-1}{\mathop \sum }}\,\ln ({{R}_{i}}-d)=n\ln (a)+\ln (b)\underset{i=n}{\overset{2n-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \\ & {{S}_{3}}(d)= & \underset{i=2n}{\overset{m-1}{\mathop \sum }}\,\ln ({{R}_{i}}-d)=n\ln (a)+\ln (b)\underset{i=2n}{\overset{m-1}{\mathop \sum }}\,{{c}^{{{T}_{i}}}} \end{align} }[/math]

Modifying Eqns. (eq9), (eq10) and (eq11) as functions of [math]\displaystyle{ d }[/math] yields:

[math]\displaystyle{ \begin{align} & c(d)= & {{\left[ \frac{{{S}_{3}}(d)-{{S}_{2}}(d)}{{{S}_{2}}(d)-{{S}_{1}}(d)} \right]}^{\tfrac{1}{n\cdot I}}} \\ & a(d)= & {{e}^{\left[ \tfrac{1}{n}\left( {{S}_{1}}(d)+\tfrac{{{S}_{2}}(d)-{{S}_{1}}(d)}{1-{{[c(d)]}^{n\cdot I}}} \right) \right]}} \\ & b(d)= & {{e}^{\left[ \tfrac{\left[ {{S}_{2}}(d)-{{S}_{1}}(d) \right]\left[ {{[c(d)]}^{I}}-1 \right]}{{{\left[ 1-{{[c(d)]}^{n\cdot I}} \right]}^{2}}} \right]}} \end{align} }[/math]

where [math]\displaystyle{ I }[/math] is the time interval increment. At this point, you can use the initial constraint of:

[math]\displaystyle{ d+ab=\text{original level of reliability at }T=0 }[/math]

Now there are four equations, Eqns. (eq17), (eq18), (eq19) and (eq20), and four unknowns, [math]\displaystyle{ a }[/math] , [math]\displaystyle{ b }[/math] , [math]\displaystyle{ c }[/math] and [math]\displaystyle{ d }[/math] . The simultaneous solution of these equations yields the four initial values for the parameters of the Modified Gompertz model. This procedure is similar to the one discussed before. It starts by using initial estimates of the parameters, [math]\displaystyle{ a }[/math] , [math]\displaystyle{ b }[/math] , [math]\displaystyle{ c }[/math] and [math]\displaystyle{ d }[/math] , denoted as [math]\displaystyle{ g_{1}^{(0)}, }[/math] [math]\displaystyle{ g_{2}^{(0)}, }[/math] [math]\displaystyle{ g_{3}^{(0)}, }[/math] and [math]\displaystyle{ g_{4}^{(0)}, }[/math] where [math]\displaystyle{ ^{(0)} }[/math] is the iteration number.
The Taylor series expansion approximates the mean response, [math]\displaystyle{ f({{T}_{i}},\delta ) }[/math] , around the starting values, [math]\displaystyle{ g_{1}^{(0)}, }[/math] [math]\displaystyle{ g_{2}^{(0)}, }[/math] [math]\displaystyle{ g_{3}^{(0)} }[/math] and [math]\displaystyle{ g_{4}^{(0)} }[/math] . For the [math]\displaystyle{ {{i}^{th}} }[/math] observation:

[math]\displaystyle{ f({{T}_{i}},\delta )\simeq f({{T}_{i}},{{g}^{(0)}})+\underset{k=1}{\overset{p}{\mathop \sum }}\,{{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}}\cdot ({{\delta }_{k}}-g_{k}^{(0)}) }[/math]

where:

[math]\displaystyle{ {{g}^{(0)}}=\left[ \begin{matrix} g_{1}^{(0)} \\ g_{2}^{(0)} \\ g_{3}^{(0)} \\ g_{4}^{(0)} \\ \end{matrix} \right] }[/math]

Let:

[math]\displaystyle{ \begin{align} & f_{i}^{(0)}= & f({{T}_{i}},{{g}^{(0)}}) \\ & \nu _{k}^{(0)}= & ({{\delta }_{k}}-g_{k}^{(0)}) \\ & D_{ik}^{(0)}= & {{\left[ \frac{\partial f({{T}_{i}},\delta )}{\partial {{\delta }_{k}}} \right]}_{\delta ={{g}^{(0)}}}} \end{align} }[/math]

Therefore:

[math]\displaystyle{ {{Y}_{i}}=f_{i}^{(0)}+\underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)} }[/math]

or by shifting [math]\displaystyle{ f_{i}^{(0)} }[/math] to the left of the equation:

[math]\displaystyle{ Y_{i}^{(0)}-f_{i}^{(0)}=\underset{k=1}{\overset{p}{\mathop \sum }}\,D_{ik}^{(0)}\nu _{k}^{(0)} }[/math]

In matrix form, this is given by:

[math]\displaystyle{ {{Y}^{(0)}}\simeq {{D}^{(0)}}{{\nu }^{(0)}} }[/math]

where:

[math]\displaystyle{ {{Y}^{(0)}}=\left[ \begin{matrix} {{Y}_{1}}-f_{1}^{(0)} \\ . \\ . \\ {{Y}_{N}}-f_{N}^{(0)} \\ \end{matrix} \right]=\left[ \begin{matrix} {{Y}_{1}}-g_{4}^{(0)}+g_{1}^{(0)}g_{2}^{(0)g_{3}^{(0){{T}_{1}}}} \\ . \\ . \\ {{Y}_{N}}-g_{4}^{(0)}+g_{1}^{(0)}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} \\ \end{matrix} \right] }[/math]

[math]\displaystyle{ \begin{align} & {{D}^{(0)}}= & \left[ \begin{matrix} D_{11}^{(0)} & D_{12}^{(0)} & D_{13}^{(0)} & D_{14}^{(0)} \\ . & . & . & . \\ . & . & . & . \\ D_{N1}^{(0)} & D_{N2}^{(0)} & D_{N3}^{(0)} & D_{N4}^{(0)} \\ \end{matrix} \right] \\ & = & \left[ \begin{matrix} g_{2}^{(0)g_{3}^{(0){{T}_{1}}}} & \tfrac{g_{1}^{(0)}}{g_{2}^{(0)}}g_{3}^{(0){{T}_{1}}}g_{2}^{(0)g_{3}^{(0){{T}_{1}}}} & \tfrac{g_{1}^{(0)}}{g_{3}^{(0)}}g_{3}^{(0){{T}_{1}}}\ln (g_{2}^{(0)}){{T}_{1}}g_{2}^{(0)g_{3}^{(0){{T}_{1}}}} & 1 \\ . & . & . & . \\ . & . & . & . \\ g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & \tfrac{g_{1}^{(0)}}{g_{2}^{(0)}}g_{3}^{(0){{T}_{N}}}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & \tfrac{g_{1}^{(0)}}{g_{3}^{(0)}}g_{3}^{(0){{T}_{N}}}\ln (g_{2}^{(0)}){{T}_{N}}g_{2}^{(0)g_{3}^{(0){{T}_{N}}}} & 1 \\ \end{matrix} \right] \end{align} }[/math]

[math]\displaystyle{ {{\nu }^{(0)}}=\left[ \begin{matrix} g_{1}^{(0)} \\ g_{2}^{(0)} \\ g_{3}^{(0)} \\ g_{4}^{(0)} \\ \end{matrix} \right] }[/math]

The same reasoning as before is followed here, and the estimate of the parameters [math]\displaystyle{ {{\nu }^{(0)}} }[/math] is given by:

[math]\displaystyle{ {{\widehat{\nu }}^{(0)}}={{\left( {{D}^{{{(0)}^{T}}}}{{D}^{(0)}} \right)}^{-1}}{{D}^{{{(0)}^{T}}}}{{Y}^{(0)}} }[/math]

The revised estimated regression coefficients in matrix form are:

[math]\displaystyle{ {{g}^{(1)}}={{g}^{(0)}}+{{\widehat{\nu }}^{(0)}} }[/math]

To see if the revised regression coefficients will lead to a reasonable result, the least squares criterion measure, , should be checked. According to the Least Squares Principle, the solution to the values of the parameters are those values that minimize [math]\displaystyle{ Q }[/math] . With the starting coefficients, [math]\displaystyle{ {{g}^{(0)}} }[/math] , [math]\displaystyle{ Q }[/math] is:

[math]\displaystyle{ Q }[/math]

[math]\displaystyle{ {{Q}^{(0)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(0)}}) \right)}^{2}} }[/math]

With the coefficients at the end of the first iteration, [math]\displaystyle{ {{g}^{(1)}} }[/math] , [math]\displaystyle{ Q }[/math] is:

[math]\displaystyle{ {{Q}^{(1)}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(1)}}) \right)}^{2}} }[/math]

For the Gauss-Newton method to work properly, and to satisfy the Least Squares Principle, the relationship [math]\displaystyle{ {{Q}^{(k+1)}}\lt {{Q}^{(k)}} }[/math] has to hold for all [math]\displaystyle{ k }[/math] , meaning that [math]\displaystyle{ {{g}^{(k+1)}} }[/math] gives a better estimate than [math]\displaystyle{ {{g}^{(k)}} }[/math] . The problem is not yet completely solved. Now [math]\displaystyle{ {{g}^{(1)}} }[/math] are the starting values, producing a new set of values [math]\displaystyle{ {{g}^{(2)}}. }[/math] The process is continued until the following relationship has been satisfied.

[math]\displaystyle{ {{Q}^{(s-1)}}-{{Q}^{(s)}}\simeq 0 }[/math]

As mentioned previously, when using the Gauss-Newton method or some other estimation procedure, it is advisable to try several sets of starting values to make sure that the solution gives relatively consistent results. Note that RGA uses a different analysis method called the Levenberg-Marquardt. This method utilizes the best features of the Gauss-Newton method and the method of the steepest descent, and occupies a middle ground between these two methods.

Confidence Bounds

The approximate reliability confidence bounds under the Modified Gompertz model can be obtained using nonlinear regression. Additionally, the reliability is always between [math]\displaystyle{ 0 }[/math] and [math]\displaystyle{ 1 }[/math] . In order to keep the endpoints of the confidence interval, the logit transformation can be used to obtain the confidence bounds on reliability.

[math]\displaystyle{ CB=\frac{{{{\hat{R}}}_{i}}}{{{{\hat{R}}}_{i}}+(1-{{{\hat{R}}}_{i}}){{e}^{\pm {{z}_{\alpha }}{{{\hat{\sigma }}}_{R}}/\left[ {{{\hat{R}}}_{i}}(1-{{{\hat{R}}}_{i}}) \right]}}} }[/math]

[math]\displaystyle{ {{\hat{\sigma }}^{2}}=\frac{SSE}{n-p} }[/math]

where [math]\displaystyle{ p }[/math] is the total number of groups (in this case 4) and [math]\displaystyle{ n }[/math] is the total number of items in each group.

Example 3

A reliability growth data set is given in Table 7.4, columns 1 and 2. Find the Modified Gompertz curve that represents the data and plot it comparatively with the raw data.

Table 7.4 - The development time versus observed reliability data and predicted reliabilities

Time(months)	Raw Data Reliability(%)	Gompertz Reliability(%)	Logistic Reliability(%)	Modified Gompertz Reliability(%)
0	31.00	25.17	22.70	31.18
1	35.50	38.33	38.10	35.08
2	49.30	51.35	56.40	49.92
3	70.10	62.92	73.00	69.23
4	83.00	72.47	85.00	83.72
5	92.20	79.94	93.20	92.06
6	96.40	85.59	96.10	96.29
7	98.60	89.75	98.10	98.32
8	99.00	92.76	99.10	99.27

Solution
To determine the parameters of the Modified Gompertz curve, use:

[math]\displaystyle{ \begin{align} & {{S}_{1}}(d)= & \underset{i=0}{\overset{2}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ & {{S}_{2}}(d)= & \underset{i=3}{\overset{5}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ & {{S}_{3}}(d)= & \underset{i=6}{\overset{8}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \end{align} }[/math]

[math]\displaystyle{ c(d)={{\left[ \frac{{{S}_{3}}(d)-{{S}_{2}}(d)}{{{S}_{2}}(d)-{{S}_{1}}(d)} \right]}^{\tfrac{1}{3}}} }[/math]

[math]\displaystyle{ a(d)={{e}^{\left[ \tfrac{1}{3}\left( {{S}_{1}}(d)+\tfrac{{{S}_{2}}(d)-{{S}_{1}}(d)}{1-{{[c(d)]}^{3}}} \right) \right]}} }[/math]

[math]\displaystyle{ b(d)={{e}^{\left[ \tfrac{({{S}_{2}}(d)-{{S}_{1}}(d))(c(d)-1)}{{{\left[ 1-{{[c(d)]}^{3}} \right]}^{2}}} \right]}} }[/math]

and:

[math]\displaystyle{ {{R}_{0}}=d+a(d)\cdot b(d) }[/math]

where [math]\displaystyle{ {{R}_{0}}=31% }[/math] . Then, Eqn. (eq27) may be rewritten as:

[math]\displaystyle{ d-31+a(d)\cdot b(d)=0 }[/math]

Eqns. (eq24), (eq25), (eq26) and (eq28) can now be solved simultaneously. One method for solving these equations numerically is to substitute different values of [math]\displaystyle{ d }[/math] , which must be less than [math]\displaystyle{ {{R}_{0}} }[/math] , into Eqn. (eq28) and plot along the y-axis with the value of [math]\displaystyle{ d }[/math] along the x-axis. The value of [math]\displaystyle{ d }[/math] can then be read from the x-intercept. This can be repeated for greater accuracy using smaller and smaller increments of [math]\displaystyle{ d }[/math] . Once the desired accuracy on [math]\displaystyle{ d }[/math] has been achieved, the value of [math]\displaystyle{ d }[/math] can then be substituted into Eqns. (eq24), (eq25) and (eq26). Now [math]\displaystyle{ a }[/math] , [math]\displaystyle{ b }[/math] and [math]\displaystyle{ c }[/math] can be calculated. For this case, the initial estimates of the parameters are:

[math]\displaystyle{ \begin{align} & \widehat{a}= & 69.324 \\ & \widehat{b}= & 0.002524 \\ & \widehat{c}= & 0.46012 \\ & \widehat{d}= & 30.825 \end{align} }[/math]

Now, since the initial values have been determined, the Gauss-Newton method can be used. Therefore, substituting [math]\displaystyle{ {{Y}_{i}}={{R}_{i}}, }[/math] [math]\displaystyle{ g_{1}^{(0)}=69.324, }[/math] [math]\displaystyle{ g_{2}^{(0)}=0.002524, }[/math] [math]\displaystyle{ g_{3}^{(0)}=0.46012, }[/math] and [math]\displaystyle{ g_{4}^{(0)}=30.825 }[/math] , [math]\displaystyle{ {{Y}^{(0)}},{{D}^{(0)}}, }[/math] [math]\displaystyle{ {{\nu }^{(0)}} }[/math] become:

[math]\displaystyle{ {{Y}^{(0)}}=\left[ \begin{matrix} 0.000026 \\ 0.253873 \\ -1.062940 \\ 0.565690 \\ -0.845260 \\ 0.096737 \\ 0.076450 \\ 0.238155 \\ -0.320890 \\ \end{matrix} \right] }[/math]

[math]\displaystyle{ {{D}^{(0)}}=\left[ \begin{matrix} 0.002524 & 69.3240 & 0.0000 & 1 \\ 0.063775 & 805.962 & -26.4468 & 1 \\ 0.281835 & 1638.82 & -107.552 & 1 \\ 0.558383 & 1493.96 & -147.068 & 1 \\ 0.764818 & 941.536 & -123.582 & 1 \\ 0.883940 & 500.694 & -82.1487 & 1 \\ 0.944818 & 246.246 & -48.4818 & 1 \\ 0.974220 & 116.829 & -26.8352 & 1 \\ 0.988055 & 54.5185 & -14.3117 & 1 \\ \end{matrix} \right] }[/math]

[math]\displaystyle{ {{\nu }^{(0)}}=\left[ \begin{matrix} g_{1}^{(0)} \\ g_{2}^{(0)} \\ g_{3}^{(0)} \\ g_{4}^{(0)} \\ \end{matrix} \right]=\left[ \begin{matrix} 69.324 \\ 0.002524 \\ 0.46012 \\ 30.825 \\ \end{matrix} \right] }[/math]

The estimate of the parameters [math]\displaystyle{ {{\nu }^{(0)}} }[/math] is given by:

[math]\displaystyle{ \begin{align} & {{\widehat{\nu }}^{(0)}}= & {{\left( {{D}^{{{(0)}^{T}}}}{{D}^{(0)}} \right)}^{-1}}{{D}^{{{(0)}^{T}}}}{{Y}^{(0)}} \\ & = & \left[ \begin{matrix} -0.275569 \\ -0.000549 \\ -0.003202 \\ 0.209458 \\ \end{matrix} \right] \end{align} }[/math]

The revised estimated regression coefficients in matrix form are given by:

[math]\displaystyle{ \begin{align} & {{g}^{(1)}}= & {{g}^{(0)}}+{{\widehat{\nu }}^{(0)}}. \\ & = & \left[ \begin{matrix} 69.324 \\ 0.002524 \\ 0.46012 \\ 30.825 \\ \end{matrix} \right]+\left[ \begin{matrix} -0.275569 \\ -0.000549 \\ -0.003202 \\ 0.209458 \\ \end{matrix} \right] \\ & = & \left[ \begin{matrix} 69.0484 \\ 0.00198 \\ 0.45692 \\ 31.0345 \\ \end{matrix} \right] \end{align} }[/math]

With the starting coefficients [math]\displaystyle{ {{g}^{(0)}} }[/math] , [math]\displaystyle{ Q }[/math] is:

[math]\displaystyle{ \begin{align} & {{Q}^{(0)}}= & \underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(0)}}) \right)}^{2}} \\ & = & 2.403672 \end{align} }[/math]

With the coefficients at the end of the first iteration, [math]\displaystyle{ {{g}^{(1)}} }[/math] , [math]\displaystyle{ Q }[/math] is:

[math]\displaystyle{ \begin{align} & {{Q}^{(1)}}= & \underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left[ {{Y}_{i}}-f\left( {{T}_{i}},{{g}^{(1)}} \right) \right]}^{2}} \\ & = & 2.073964 \end{align} }[/math]

Therefore:

[math]\displaystyle{ {{Q}^{(1)}}\lt {{Q}^{(0)}} }[/math]

Hence, the Gauss-Newton method works in the right direction. The iterations are continued until the relationship of Eqn. (critir) has been satisfied. Using RGA, the estimators of the parameters are:

[math]\displaystyle{ \begin{align} & \widehat{a}= & 0.6904 \\ & \widehat{b}= & 0.0020 \\ & \widehat{c}= & 0.4567 \\ & \widehat{d}= & 0.3104 \end{align} }[/math]

Therefore, the Modified Gompertz model is:

[math]\displaystyle{ R=0.3104+(0.6904){{(0.0020)}^{{{0.4567}^{T}}}} }[/math]

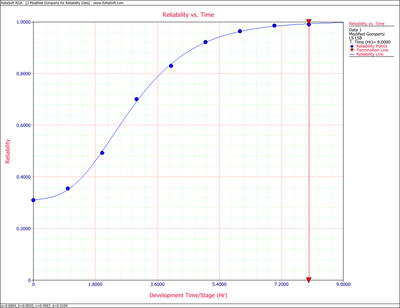
Using Eqn. (eq29), the predicted reliability is plotted in the following figure along with the raw data. It can be seen from the plot in Figure MGomp1 that the Modified Gompertz curve represents the data very well.

Modified Gompertz reliability growth curve.