Template:Warranty analysis-nevada format
Warranty Analysis (Nevada Format)
The Nevada Format allows the user to convert shipping and warranty return data into the standard reliability data form of failures and suspensions so that it can easily be analyzed with traditional life data analysis methods. For each time period in which a number of products are shipped, there will be a certain number of returns or failures in subsequent time periods, while the rest of the population that was shipped will continue to operate in the following time periods. For example, if 500 units are shipped in May, and 10 of those units are warranty returns in June, that is equivalent to 10 failures at a time of one month. The other 450 units will go on to operate and possibly fail in months that follow. At the end of the analysis period, all of the units that were shipped and have not failed in the time since shipment are considered to be suspensions. This process is repeated for each shipment and the results tabulated for each particular failure and suspension time prior to reliability analysis. This process may sound confusing, but it is actually just a matter of careful bookkeeping, and is illustrated with the example that follows.
Example 2
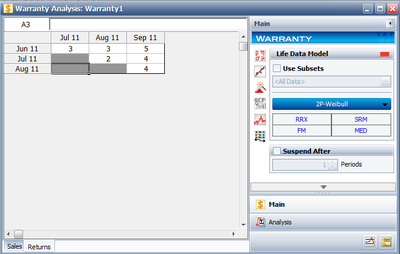
A company keeps track of its shipments and warranty returns on a month-by-month basis. The data format that the company uses is the Nevada format. Following is a table for shipments in June, July, and August, and the warranty returns through September:
| RETURNS | ||||
| SHIP | Jul. 2010 | Aug. 2010 | Sep. 2010 | |
| Jun. 2010 | 100 | 3 | 3 | 5 |
| Jul. 2010 | 140 | - | 2 | 4 |
| Aug. 2010 | 150 | - | - | 4 |
Convert this information to life data, and determine the parameters for a two-parameter Weibull distribution.
Solution to Example 2
We will examine the data month by month. In June 100 units were sold, and in July three of these units were returned. This gives three failures at one month for the June shipment, which we will denote as [math]\displaystyle{ {{F}_{JUN,1}}=3 }[/math] . Likewise, three failures occurred in August and five occurred in September for this shipment, or [math]\displaystyle{ {{F}_{JUN,2}}=3 }[/math] and [math]\displaystyle{ {{F}_{JUN,3}}=5. }[/math] Consequently, at the end of our three-month analysis period, there were a total of 11 failures for the 100 units shipped in June. This means that 89 units are presumably still operating, and can be considered suspensions at three months, or [math]\displaystyle{ {{S}_{JUN,3}}=89 }[/math] . For the shipment of 140 in July, two were returned the following month, or [math]\displaystyle{ {{F}_{JUL,1}}=2 }[/math] , and four more were returned the month after that, or [math]\displaystyle{ {{F}_{JUL,2}}=4. }[/math] After two months, there are 134 ( [math]\displaystyle{ 140-2-4=134 }[/math] ) units from the July shipment still operating, or [math]\displaystyle{ {{S}_{JUL,2}}=134 }[/math]. For the final shipment of 150 in August, four fail in September, or [math]\displaystyle{ {{F}_{AUG,1}}=4 }[/math], with the remaining 146 units being suspensions at one month, or [math]\displaystyle{ {{S}_{AUG,1}}=146 }[/math] .
It is now a simple matter to add up the number of failures for 1, 2, and 3 months, then add the suspensions to get our reliability data set:
To perform this analysis using the Warranty Analysis tool in Weibull++, create a Warranty Analysis Folio and choose I want to enter data inNevada format in the Project Wizard.
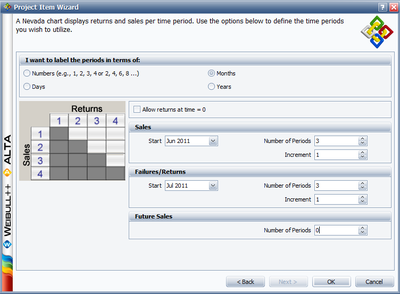
The next window allows you to specify the time units used. For this example select Months under I want to use the following unit type for each period and enter the Start month and Number of Periods and Increment number for the sales data and failure/return data as follows:
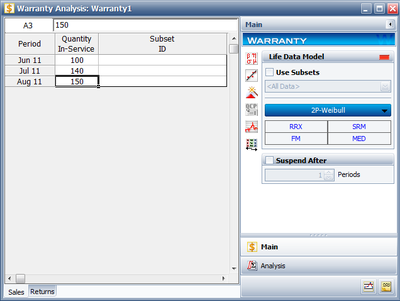
The sales data are entered as follows:
The return data are entered as follows:
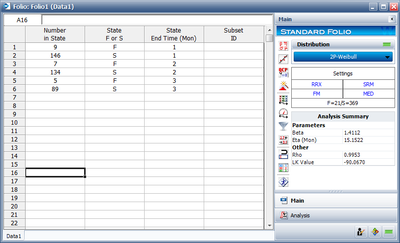
The data can now be analyzed. Select two-parameter Weibull as the distribution type and MLE as the analysis method and click the Calculate button. The estimated parameters are [math]\displaystyle{ \widehat{\beta }=2.49 }[/math] and [math]\displaystyle{ \widehat{\eta }=6.70. }[/math]
Even though this step is not required for the analysis, the data can also be transferred to a Weibull++ data sheet for illustrative purposes or for ancillary analysis. This can be done by clicking the Transfer Life Data to New Folio button:
[math]\displaystyle{ }[/math]
or choosing this option under the Data menu.
The equivalent Times-to-failure folio is as follows: