Template:Weibull parameters Rank Regression on Y

Rank Regression on Y

Performing rank regression on Y requires that a straight line mathematically be fitted to a set of data points such that the sum of the squares of the vertical deviations from the points to the line is minimized. This is in essence the same methodology as the probability plotting method, except that we use the principle of least squares to determine the line through the points, as opposed to just eyeballing it. The first step is to bring our function into a linear form. For the two-parameter Weibull distribution, the (cumulative density function) is:

[math]\displaystyle{ F(T)=1-e^{-\left( \frac{T}{\eta }\right) ^{\beta }} (Fw) }[/math]

Taking the natural logarithm of both sides of the equation yields:

[math]\displaystyle{ \ln[ 1-F(T)] =-( \frac{T}{\eta }) ^{\beta } }[/math]

[math]\displaystyle{ \ln{ -\ln[ 1-F(T)]} =\beta \ln ( \frac{T}{ \eta }) }[/math]

or:

[math]\displaystyle{ \ln \{ -\ln[ 1-F(T)]\} =-\beta \ln (\eta )+\beta \ln (T) EQNREF logw }[/math]

Now let:

[math]\displaystyle{ y = \ln \{ -\ln[ 1-F(T)]\} ( yw ) }[/math]

[math]\displaystyle{ a = − βln(\eta) }[/math] (aw)

and:

[math]\displaystyle{ b= \beta }[/math] ( bw )

which results in the linear equation of:

[math]\displaystyle{ y=a+bx }[/math]

The least squares parameter estimation method (also known as regression analysis) was discussed in Chapter 3 and the following equations for regression on Y were derived in Appendix A:

[math]\displaystyle{ \hat{a}=\frac{\sum\limits_{i=1}^{N}y_{i}}{N}-\hat{b}\frac{ \sum\limits_{i=1}^{N}x_{i}}{N}=\bar{y}-\hat{b}\bar{x} EQNREF aaw }[/math]

and:

[math]\displaystyle{ \hat{b}={\frac{\sum\limits_{i=1}^{N}x_{i}y_{i}-\frac{\sum \limits_{i=1}^{N}x_{i}\sum\limits_{i=1}^{N}y_{i}}{N}}{\sum \limits_{i=1}^{N}x_{i}^{2}-\frac{\left( \sum\limits_{i=1}^{N}x_{i}\right) ^{2}}{N}}} EQNREF bbw }[/math]

In this case the equations for y_i and x_i are:

[math]\displaystyle{ y_{i}=\ln \left\{ -\ln [1-F(T_{i})]\right\} , }[/math]

and:

x_i = ln(T_i).

The [math]\displaystyle{ F(T_{i})^{\prime }s }[/math] are estimated from the median ranks.

Once [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math] are obtained, then [math]\displaystyle{ \hat{\beta } }[/math] and [math]\displaystyle{ \hat{\eta } }[/math] can easily be obtained from Eqns. (EQNREF aw ) and (\ref {bw}).

The Correlation Coefficient

The correlation coefficient is defined as follows:

[math]\displaystyle{ \rho ={\frac{\sigma _{xy}}{\sigma _{x}\sigma _{y}}} }[/math]

where, σ_{x y} = covariance of and , σ_x = standard deviation of , and σ_y = standard deviation of . The estimator of ρ is the sample correlation coefficient, [math]\displaystyle{ \hat{\rho} }[/math], given by:

[math]\displaystyle{ \hat{\rho}=\frac{\sum\limits_{i=1}^{N}(x_{i}-\overline{x})(y_{i}-\overline{y} )}{\sqrt{\sum\limits_{i=1}^{N}(x_{i}-\overline{x})^{2}\cdot \sum\limits_{i=1}^{N}(y_{i}-\overline{y})^{2}}} EQNREF RHOw }[/math]

Example 3

Consider the data in Example 1, where six units were tested to failure and the following failure times were recorded: 16, 34, 53, 75, 93 and 120 hours. Estimate the parameters and the correlation coefficient using rank regression on Y, assuming that the data follow the two-parameter Weibull distribution.

Solution to Example 3

Construct a table as shown below.

Table 6.1 - Least Squares Analysis
[math]\displaystyle{ N }[/math]	[math]\displaystyle{ T_{i} }[/math]	[math]\displaystyle{ ln(T_{i}) }[/math]	[math]\displaystyle{ F(T_i) }[/math]	[math]\displaystyle{ y_{i} }[/math]	[math]\displaystyle{ (ln{T_i})^2 }[/math]	[math]\displaystyle{ {y_i}^2 }[/math]	[math]\displaystyle{ (ln{T_i})y_i }[/math]
1	16	2.7726	0.1091	-2.1583	7.6873	4.6582	-5.9840
2	34	3.5264	0.2645	-1.1802	12.4352	1.393	-4.1620
3	53	3.9703	0.4214	-0.6030	15.7632	0.3637	-2.3943
4	75	4.3175	0.5786	-0.146	18.6407	0.0213	-0.6303
5	93	4.5326	0.7355	0.2851	20.5445	0.0813	1.2923
6	120	4.7875	0.8909	0.7955	22.9201	0.6328	3.8083
[math]\displaystyle{ \sum }[/math]		23.9068		-3.007	97.9909	7.1502	-8.0699

Utilizing the values from Table 6.1, calculate [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math] using Eqns. (EQNREF aaw ) and (EQNREF bbw ):

[math]\displaystyle{ \hat{b} =\frac{\sum\limits_{i=1}^{6}(\ln T_{i})y_{i}-(\sum\limits_{i=1}^{6}\ln T_{i})(\sum\limits_{i=1}^{6}y_{i})/6}{ \sum\limits_{i=1}^{6}(\ln T_{i})^{2}-(\sum\limits_{i=1}^{6}\ln T_{i})^{2}/6} }[/math]

[math]\displaystyle{ \hat{b}=\frac{-8.0699-(23.9068)(-3.0070)/6}{97.9909-(23.9068)^{2}/6} }[/math]

or

[math]\displaystyle{ \hat{b}=1.4301 }[/math]

and:

[math]\displaystyle{ \hat{a}=\overline{y}-\hat{b}\overline{T}=\frac{\sum \limits_{i=1}^{N}y_{i}}{N}-\hat{b}\frac{\sum\limits_{i=1}^{N}\ln T_{i}}{N } }[/math]

or:

[math]\displaystyle{ \hat{a}=\frac{(-3.0070)}{6}-(1.4301)\frac{23.9068}{6}=-6.19935 }[/math]

Therefore, from Eqn. (EQNREF bw ):

[math]\displaystyle{ \hat{\beta }=\hat{b}=1.4301 }[/math]

and from Eqn. (EQNREF aw ):

[math]\displaystyle{ \hat{\eta }=e^{-\frac{\hat{a}}{\hat{b}}}=e^{-\frac{(-6.19935)}{ 1.4301}} }[/math]

or:

[math]\displaystyle{ \hat{\eta }=76.318\text{ hr} }[/math]

The correlation coefficient can be estimated using Eqn. (EQNREF RHOw ):

[math]\displaystyle{ \hat{\rho }=0.9956 }[/math]

The above example can be repeated using Weibull++. Start Weibull++ and create a new Data Folio.

Select the Times-to-failure data option.

The effect of the Weibull shape parameter on the [math]\displaystyle{ pdf }[/math].

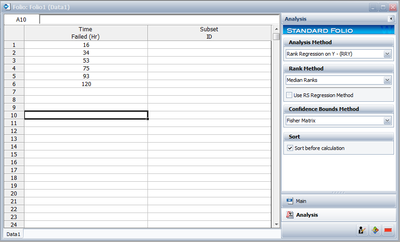
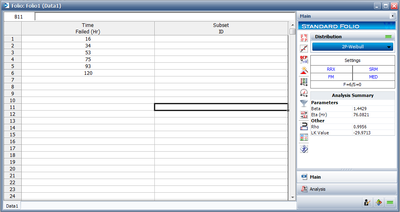
Enter the times-to-failure in the datasheet (ignore the Subset ID column), as shown next. The times-to-failure need not be sorted, Weibull++ will automatically sort the data.

Select the desired method of analysis. Note that we are assuming that the underlying distribution is the Weibull, so make sure that the Weibull distribution is selected. Under Parameters/Type on the Main page, select 2.

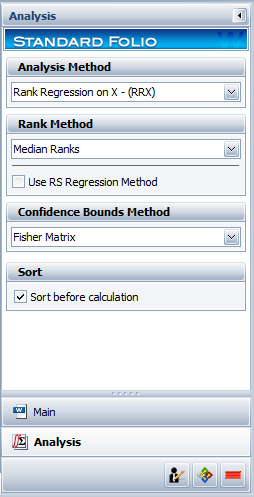
Also, so that you get the same results as this example, switch to the Analysis page and make sure you are using the Rank Regression on Y (RRY) calculation method with this example, as shown next.

Note that this can also be done from the Main page by clicking the left bottom box under the Results area. Each time you click that box you will see the method switch between MLE, RRX, and RRY. Click the Calculate icon,

or select Calculate from the Data menu. The results will appear in the Data Folio's Results area. The next figure shows the results for this example.

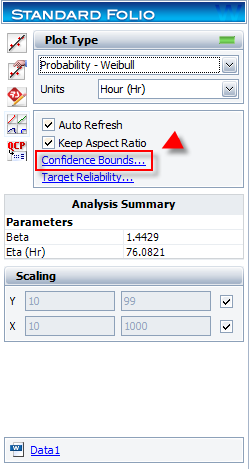
You can now plot the results by clicking the Plot icon,

or by selecting Plot Probability from the Data menu.

The Weibull probability plot for these data is shown next.

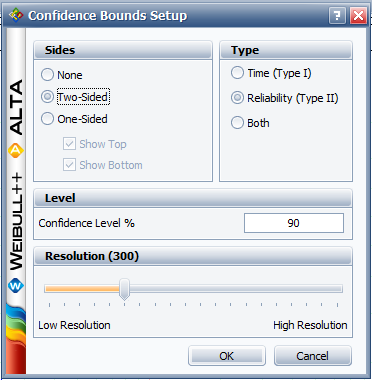
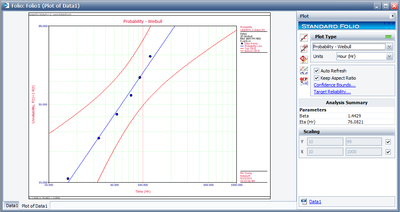
The confidence bounds, as determined from the Fisher matrix, can also be plotted. Select Confidence Bounds from the Plot menu, choose Two-Sided under Sides, Reliability (Type II) under Type and enter 90 for the Confidence level.

The plot will appear as follows,

If desired, the Weibull [math]\displaystyle{ pdf }[/math] representing these data can be written as:

[math]\displaystyle{ f(T)={\frac{\beta }{\eta }}\left( {\frac{T}{\eta }}\right) ^{\beta -1}e^{-\left( {\frac{T}{\eta }}\right) ^{\beta }} }[/math]

or:

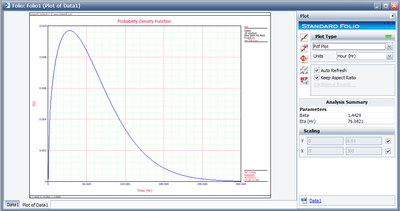
[math]\displaystyle{ f(T)={\frac{1.4302}{76.317}}\left( {\frac{T}{76.317}}\right) ^{0.4302}e^{-\left( {\frac{T}{76.317}}\right) ^{1.4302}} }[/math] You can also plot the Weibull by selecting Pdf Plot from the Plot Type drop-down menu on the control panel to the right of the plot area.

From this point on, different results, reports and plots can be obtained.