Template:ReliabilityFunction

The Reliability Function

The reliability function can be derived using the previous definition of the cumulative distribution function. The probability of an event happening by time [math]\displaystyle{ t }[/math] is given by:

[math]\displaystyle{ F(t)=\int_{0,\gamma}^{t}f(s)ds }[/math]

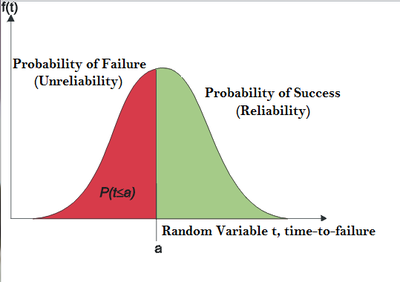
In particular, this represents the probability of a unit failing by time [math]\displaystyle{ t }[/math]. From this, we obtain the most commonly used function in reliability engineering, the reliability function, which represents the probability of success of a unit in undertaking a mission of a prescribed duration. To mathematically show this, we first define the unreliability function, [math]\displaystyle{ Q(t) }[/math], which is the probability of failure, or the probability that our time-to-failure is in the region of [math]\displaystyle{ 0 }[/math] (or [math]\displaystyle{ \gamma }[/math]) and [math]\displaystyle{ t }[/math]. So from the previous equation:

[math]\displaystyle{ F(t)=Q(t)=\int_{0,\gamma}^{t}f(s)ds }[/math]

In this situation, there are only two states that can occur: success or failure. These two states are also mutually exclusive. Since reliability and unreliability are the probabilities of these two mutually exclusive states, the sum of these probabilities is always equal to unity. So then:

[math]\displaystyle{ \begin{align} Q(t)+R(t)& = 1 \\ R(t) & = 1-Q(t) \\ R(t) & = 1-\int_{0,\gamma}^{t}f(s)ds \\ R(t) & = \int_{t}^{\infty }f(s)ds \end{align} }[/math]

Conversely:

[math]\displaystyle{ f(t)=-\frac{d(R(t))}{dt} }[/math]