Template:Least squares estimators lloyd-l
Least Squares Estimators
To obtain least squares estimators for [math]\displaystyle{ {{R}_{\infty }} }[/math] and [math]\displaystyle{ \alpha }[/math] , the sum of squares, [math]\displaystyle{ Q }[/math] , of the deviations of the observed success-ratio, [math]\displaystyle{ {{S}_{k}}/{{n}_{k}} }[/math] , is minimized from its expected value, [math]\displaystyle{ {{R}_{\infty }}-\tfrac{\alpha }{k} }[/math] , with respect to the parameters [math]\displaystyle{ {{R}_{\infty }} }[/math] and [math]\displaystyle{ \alpha . }[/math] Therefore, [math]\displaystyle{ Q }[/math] is expressed as:
- [math]\displaystyle{ Q=\underset{k=1}{\overset{N}{\mathop \sum }}\,{{\left( \frac{{{S}_{k}}}{{{n}_{k}}}-{{R}_{\infty }}+\frac{\alpha }{k} \right)}^{2}} }[/math]
Taking the derivatives with respect to [math]\displaystyle{ {{R}_{\infty }} }[/math] and [math]\displaystyle{ \alpha }[/math] and setting equal to zero yields:
- [math]\displaystyle{ \begin{align} & \frac{\partial Q}{\partial {{R}_{\infty }}}= & -2\underset{k=1}{\overset{N}{\mathop \sum }}\,\left( \frac{{{S}_{k}}}{{{n}_{k}}}-{{R}_{\infty }}+\frac{\alpha }{k} \right)=0 \\ & \frac{\partial Q}{\partial \alpha }= & 2\underset{k=1}{\overset{N}{\mathop \sum }}\,\left( \frac{{{S}_{k}}}{{{n}_{k}}}-{{R}_{\infty }}+\frac{\alpha }{k} \right)\frac{1}{k}=0 \end{align} }[/math]
Solving Eqns. (pqprll) and (pqpall) simultaneously, the least squares estimates of [math]\displaystyle{ {{R}_{\infty }} }[/math] and [math]\displaystyle{ \alpha }[/math] are:
- [math]\displaystyle{ {{\hat{R}}_{\infty }}=\frac{\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{{{k}^{2}}}\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{{{S}_{k}}}{{{n}_{k}}}-\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k}\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{{{S}_{k}}}{k{{n}_{k}}}}{N\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{{{k}^{2}}}-{{\left( \underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k} \right)}^{2}}} }[/math]
- or:
- [math]\displaystyle{ \text{ }{{\hat{R}}_{\infty }}=\frac{\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{{{k}^{2}}}\underset{k=1}{\overset{N}{\mathop{\sum }}}\,{{R}_{k}}-\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k}\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{{{R}_{k}}}{k}}{N\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{{{k}^{2}}}-{{\left( \underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k} \right)}^{2}}} }[/math]
- and:
- [math]\displaystyle{ \hat{\alpha }=\frac{\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k}\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{{{S}_{k}}}{{{n}_{k}}}-N\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{{{S}_{k}}}{k{{n}_{k}}}}{N\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{{{k}^{2}}}-{{\left( \underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k} \right)}^{2}}} }[/math]
- or:
- [math]\displaystyle{ \hat{\alpha }=\frac{\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k}\underset{k=1}{\overset{N}{\mathop{\sum }}}\,{{R}_{k}}-N\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{{{R}_{k}}}{k}}{N\underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{{{k}^{2}}}-{{\left( \underset{k=1}{\overset{N}{\mathop{\sum }}}\,\tfrac{1}{k} \right)}^{2}}} }[/math]
Example 1
After a 20-stage reliability development test program, 20 groups of success/failure data were obtained and are given in Table 6.1. Do the following:
- 1) Fit the Lloyd-Lipow model to the data using least squares.
- 2) Plot the reliabilities predicted by the Lloyd-Lipow model along with the observed reliabilities and compare the results.
| Test Stage Number([math]\displaystyle{ k }[/math]) | Number of Tests in Stage([math]\displaystyle{ n_k }[/math]) | Number of Successful Tests([math]\displaystyle{ S_k }[/math]) | Raw Data Reliability | Lloyd-Lipow Reliability |
|---|---|---|---|---|
| 1 | 9 | 6 | 0.667 | 0.7002 |
| 2 | 9 | 5 | 0.556 | 0.7369 |
| 3 | 8 | 7 | 0.875 | 0.7552 |
| 4 | 10 | 6 | 0.600 | 0.7662 |
| 5 | 9 | 7 | 0.778 | 0.7736 |
| 6 | 10 | 8 | 0.800 | 0.7788 |
| 7 | 10 | 7 | 0.700 | 0.7827 |
| 8 | 10 | 6 | 0.600 | 0.7858 |
| 9 | 11 | 7 | 0.636 | 0.7882 |
| 10 | 11 | 9 | 0.818 | 0.7902 |
| 11 | 9 | 9 | 1.000 | 0.7919 |
| 12 | 12 | 10 | 0.833 | 0.7933 |
| 13 | 12 | 9 | 0.750 | 0.7945 |
| 14 | 11 | 8 | 0.727 | 0.7956 |
| 15 | 10 | 7 | 0.700 | 0.7965 |
| 16 | 10 | 8 | 0.800 | 0.7973 |
| 17 | 11 | 10 | 0.909 | 0.7980 |
| 18 | 10 | 9 | 0.900 | 0.7987 |
| 19 | 9 | 8 | 0.889 | 0.7992 |
| 20 | 8 | 7 | 0.875 | 0.7998 |
Solution
From Table 6.1, the least squares estimates are:
- [math]\displaystyle{ \begin{align} & \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{1}{k}= & \underset{k=1}{\overset{20}{\mathop \sum }}\,\frac{1}{k}=3.5977 \\ & \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{1}{{{k}^{2}}}= & \underset{k=1}{\overset{20}{\mathop \sum }}\,\frac{1}{{{k}^{2}}}=1.5962 \\ & \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{{{S}_{k}}}{{{n}_{k}}}= & \underset{k=1}{\overset{20}{\mathop \sum }}\,\frac{{{S}_{k}}}{{{n}_{k}}}=15.4131 \end{align} }[/math]
- and:
- [math]\displaystyle{ \underset{k=1}{\overset{N}{\mathop \sum }}\,\frac{{{S}_{k}}}{k\cdot {{n}_{k}}}=\underset{k=1}{\overset{20}{\mathop \sum }}\,\frac{{{S}_{k}}}{k\cdot {{n}_{k}}}=2.5632 }[/math]
Substituting into Eqns. (ar) and (alph) yields:
- [math]\displaystyle{ \begin{align} & {{{\hat{R}}}_{\infty }}= & \frac{(1.5962)(15.413)-(3.5977)(2.5637)}{(20)(1.5962)-{{(3.5977)}^{2}}} \\ & = & 0.8104 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & \hat{\alpha }= & \frac{(3.5977)(15.413)-(20)(2.5637)}{(20)(1.5962)-{{(3.5977)}^{2}}} \\ & = & 0.2207 \end{align} }[/math]
Therefore, the Lloyd-Lipow reliability growth model is as follows, where [math]\displaystyle{ k }[/math] is the test stage.
- [math]\displaystyle{ {{R}_{k}}=0.8104-\frac{0.2201}{k} }[/math]
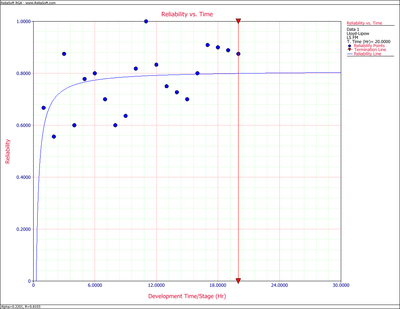
The reliabilities from the raw data and the reliabilities predicted from Eqn. (eq33) are given in the last two columns of Table 6.1. Figure llfig61 shows the plot. Based on the given data, the model cannot do much more than to basically fit a line through the middle of the points.