Template:Bounds on cumulative number of failures rsa
Bounds on Cumulative Number of Failures
Fisher Matrix Bounds
The cumulative number of failures, [math]\displaystyle{ N(t) }[/math] , must be positive, thus [math]\displaystyle{ \ln \left( N(t) \right) }[/math] is approximately treated as being normally distributed.
- [math]\displaystyle{ \frac{\ln (\widehat{N}(t))-\ln (N(t))}{\sqrt{Var\left[ \ln \widehat{N}(t) \right]}}\sim N(0,1) }[/math]
- [math]\displaystyle{ N(t)=\widehat{N}(t){{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\widehat{N}(t))}/\widehat{N}(t)}} }[/math]
- where:
- [math]\displaystyle{ \widehat{N}(t)=\widehat{\lambda }{{t}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \begin{align} & Var(\widehat{N}(t))= & {{\left( \frac{\partial N(t)}{\partial \beta } \right)}^{2}}Var(\widehat{\beta })+{{\left( \frac{\partial N(t)}{\partial \lambda } \right)}^{2}}Var(\widehat{\lambda }) \\ & & +2\left( \frac{\partial N(t)}{\partial \beta } \right)\left( \frac{\partial N(t)}{\partial \lambda } \right)cov(\widehat{\beta },\widehat{\lambda }) \end{align} }[/math]
The variance calculation is the same as Eqns. (var1), (var2) and (var3).
- [math]\displaystyle{ \begin{align} & \frac{\partial N(t)}{\partial \beta }= & \hat{\lambda }{{t}^{\widehat{\beta }}}\ln (t) \\ & \frac{\partial N(t)}{\partial \lambda }= & t\widehat{\beta } \end{align} }[/math]
Crow Bounds
- [math]\displaystyle{ \begin{array}{*{35}{l}} {{N}_{L}}(T)=\tfrac{T}{\widehat{\beta }}{{\lambda }_{i}}{{(T)}_{L}} \\ {{N}_{U}}(T)=\tfrac{T}{\widehat{\beta }}{{\lambda }_{i}}{{(T)}_{U}} \\ \end{array} }[/math]
where [math]\displaystyle{ {{\lambda }_{i}}{{(T)}_{L}} }[/math] and [math]\displaystyle{ {{\lambda }_{i}}{{(T)}_{U}} }[/math] can be obtained from Eqn. (inr).
Example 3
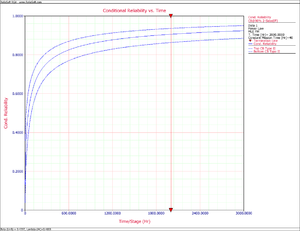
Using the data from Example 1, calculate the mission reliability at [math]\displaystyle{ t=2000 }[/math] hours and mission time [math]\displaystyle{ d=40 }[/math] hours along with the confidence bounds at the 90% confidence level.
Solution
The maximum likelihood estimates of [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] from Example 1 are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.45300 \\ & \widehat{\lambda }= & 0.36224 \end{align} }[/math]
From Eq. (reliability), the mission reliability at [math]\displaystyle{ t=2000 }[/math] for mission time [math]\displaystyle{ d=40 }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{R}(t)= & {{e}^{-\left[ \lambda {{\left( t+d \right)}^{\beta }}-\lambda {{t}^{\beta }} \right]}} \\ & = & 0.90292 \end{align} }[/math]
At the 90% confidence level and [math]\displaystyle{ T=2000 }[/math] hours, the Fisher Matrix confidence bounds for the mission reliability for mission time [math]\displaystyle{ d=40 }[/math] are given by:
- [math]\displaystyle{ CB=\frac{\widehat{R}(t)}{\widehat{R}(t)+(1-\widehat{R}(t)){{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\widehat{R}(t))}/\left[ \widehat{R}(t)(1-\widehat{R}(t)) \right]}}} }[/math]
- [math]\displaystyle{ \begin{align} & {{[\widehat{R}(t)]}_{L}}= & 0.83711 \\ & {{[\widehat{R}(t)]}_{U}}= & 0.94392 \end{align} }[/math]
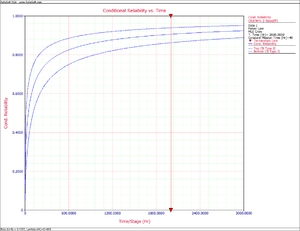
The Crow confidence bounds for the mission reliability are:
- [math]\displaystyle{ \begin{align} & {{[\widehat{R}(t)]}_{L}}= & {{[\widehat{R}(\tau )]}^{\tfrac{1}{{{\Pi }_{1}}}}} \\ & = & {{[0.90292]}^{\tfrac{1}{0.71440}}} \\ & = & 0.86680 \\ & {{[\widehat{R}(t)]}_{U}}= & {{[\widehat{R}(\tau )]}^{\tfrac{1}{{{\Pi }_{2}}}}} \\ & = & {{[0.90292]}^{\tfrac{1}{1.6051}}} \\ & = & 0.93836 \end{align} }[/math]
Figures ConfReliFish and ConfRelCrow show the Fisher Matrix and Crow confidence bounds on mission reliability for mission time [math]\displaystyle{ d=40 }[/math] .