Template:Discrete data crow rga
Discrete Data
The Crow Extended - Continuous Evaluation model also can be applied for discrete data from one-shot (success/failure) testing. In RGA 7, the Multi-Phase > Mixed Data option gives a data sheet that can accommodate data from tests where a single unit is tested for each successive configuration (individual trial-by-trial), where multiple units are tested for each successive configuration (configurations in groups) or a combination of both.
Corrective actions cannot take place at the time of failure for discrete data. With that in mind, the mixed data type does not allow for BC modes. The delayed corrective actions over time can be either fixed or unfixed, based on a subsequent implementation (I) event. So, for discrete data there are only unfixed BD modes or fixed BD modes. As a practical application, think of a multi-phase program for missile systems. Since these are one-shot items, the fixes to failure modes are delayed until at least the next trial.
Note that for calculation purposes it is required to have at least three failures in the first interval. If that is not the case, then the data set needs to be grouped until this requirement is met before calculating. RGA 7 performs this operation in the background.
Example 3
A one-shot system underwent reliability growth development for a total of 20 trials. The test was performed as a combination of configuration in groups and individual trial-by-trial. Table 10.4 shows the obtained data set. The "Failures in Interval" column specifies the number of failures that occurred in each interval and the "Cumulative Trials" column specifies the cumulative number of trials at the end of that interval.
The table also gives the classifications of the failure modes. There are 5 BD modes. Of these 5 modes, 2 are corrected during the test (BD3 and BD4) and 3 have not been corrected by time [math]\displaystyle{ T=20 }[/math] (BD1, BD2 and BD5). Do the following:
- 1) Calculate the parameters of the Crow Extended - Continuous Evaluation model.
- 2) Calculated the demonstrated reliability at the end of the test.
- 3) Calculate parameter [math]\displaystyle{ p }[/math] .
- 4) Calculate the unfixed BD mode failure probability.
- 5) Calculate the nominal growth potential factor.
- 6) Calculate the nominal average effectiveness factor.
- 7) Calculate the discovery failure intensity function at the end of the test.
- 8) Calculate the nominal projected reliability at the end of the test.
- 9) Calculate the nominal growth potential reliability at the end of the test.
Solution
- 1) Figure MIxed data shows the data for Example 3 as entered in RGA 7.
The parameters [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \lambda }[/math] are calculated as follows (the calculations for these parameters are presented in detail in Chapter 5, Section 5.1.1):
- [math]\displaystyle{ \widehat{\beta }=0.8572 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.4602 }[/math]
- 2) The corresponding demonstrated unreliability is calculated as:
- [math]\displaystyle{ {{f}_{D}}=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, the instantaneous unreliability at the end of the test (or [math]\displaystyle{ T=20) }[/math] is equal to:
- [math]\displaystyle{ {{f}_{D}}(20)=0.8572\cdot 0.4602\cdot {{20}^{0.8572-1}}=0.2572 }[/math]
The demonstrated reliability is:
- [math]\displaystyle{ \begin{align} & {{R}_{D}}= & 1-{{f}_{D}} \\ & = & 1-0.2572=0.7428 \end{align} }[/math]
Note that in discrete data, we calculate reliability and not MTBF, since we are dealing with number of trials and not test time.
- 3) Assume that the following effectiveness factors are assigned to the unfixed BD modes:
- [math]\displaystyle{ \begin{matrix} \text{Classification} & \text{Mode} & \text{Effectiveness Factor} & \text{Implemented at End of Phase} \\ \text{BD} & \text{1} & \text{0}\text{.65} & \text{Phase 1} \\ \text{BD} & \text{2} & \text{0}\text{.70} & \text{Phase 1} \\ \text{BD} & \text{5} & \text{0}\text{.75} & \text{Phase 1} \\ \end{matrix} }[/math]
The parameter [math]\displaystyle{ p }[/math] is the total number of distinct unfixed BD modes at time [math]\displaystyle{ T }[/math] divided by the total number of distinct BD (fixed and unfixed) modes.
In this example:
- [math]\displaystyle{ p=\frac{3}{5}=0.6 }[/math]
- 4) The unfixed BD mode failure probability at time [math]\displaystyle{ T }[/math] is the total number of unfixed BD failures (classified at time [math]\displaystyle{ T }[/math] ) divided by the total trials. Based on Table 10.4, we have:
- 5) Based on Eqn. (Nonimal GP Factor), the nominal growth potential factor is:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{NGPFactor}}= & \underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{i}} \right)\frac{{{N}_{i}}}{T} \\ & = & \left( 1-{{d}_{1}} \right)\frac{{{N}_{1}}}{T}+\left( 1-{{d}_{2}} \right)\frac{{{N}_{2}}}{T}+\left( 1-{{d}_{5}} \right)\frac{{{N}_{5}}}{T} \\ & = & \left( 1-0.65 \right)\frac{1}{20}+\left( 1-0.70 \right)\frac{2}{20}+\left( 1-0.75 \right)\frac{1}{20} \\ & = & 0.06 \end{align} }[/math]
- 6) Using Eqn. (Average Nominal EF), the nominal average effectiveness factor is:
- [math]\displaystyle{ \begin{align} & {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ & = & \frac{0.65+0.70+0.75}{3} \\ & = & 0.70 \end{align} }[/math]
- 7) Based on Eqn. (Discovery Function), the discovery function at time [math]\displaystyle{ T }[/math] is calculated using all the first occurrences of all the BD modes, both fixed and unfixed. In our example, we calculate [math]\displaystyle{ {{\widehat{\beta }}_{BD}} }[/math] and [math]\displaystyle{ {{\widehat{\lambda }}_{BD}} }[/math] using only the unfixed BD modes and excluding the second occurrence of BD2, which results in the following:
- [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6602 }[/math]
- and:
- [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.6920 }[/math]
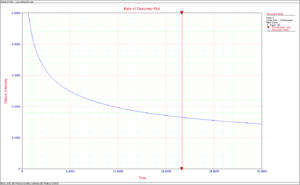
So the discovery failure intensity function at time [math]\displaystyle{ T=20 }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ & = & 0.6920\cdot 0.6602\cdot {{20}^{0.6602-1}} \\ & = & 0.16507 \end{align} }[/math]
Figure Discovery failure prob function shows the plot for the discovery failure intensity function.
- 8) Based on Eqn. (Nominal projected failure intensity), the nominal projected failure probability at time [math]\displaystyle{ T=20 }[/math] is:
- [math]\displaystyle{ \begin{align} & {{f}_{NP}}= & {{f}_{NGP}}+{{d}_{N}}h(T) \\ & = & 0.0701+0.7\cdot 0.16507 \\ & = & 0.1865 \end{align} }[/math]
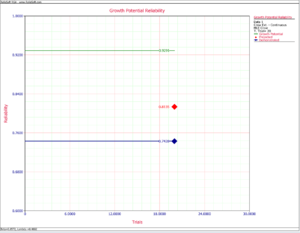
Therefore, the nominal projected reliability is:
- [math]\displaystyle{ \begin{align} & {{R}_{P}}= & 1-0.1856= \\ & = & 0.8135 \end{align} }[/math]
- 9) Based on Eqn. (Nominal Growth Potential failure intensity), the nominal growth potential unreliability is:
Based on the previous calculation for this example, we have:
- [math]\displaystyle{ \begin{align} & {{f}_{NGP}}= & 0.2572-0.2+0.06+0.7\cdot 0.6\cdot 0.16507-0.7\cdot 0.16507 \\ & = & 0.0709 \end{align} }[/math]
So the nominal growth potential reliability is:
- [math]\displaystyle{ \begin{align} & {{R}_{NGP}}= & 1-0.0709 \\ & = & 0.9291 \end{align} }[/math]
Figure GPplot shows the plot for the instantaneous demonstrated, projected and growth potential reliability.