Template:Effectiveness factor crow rga
Effectiveness Factors
As discussed in Chapter 9, it is very important to note that failure modes are rarely totally eliminated by a corrective action. After failure modes have been found and fixed, a certain percentage of the failure intensity will be removed, but a certain percentage of the failure intensity will also remain. For each BD mode, an effectiveness factor (EF) is required to estimate how effective the corrective action will be in eliminating the failure intensity due to the failure mode. The EF is the fractional decrease in a mode's failure intensity after a corrective action has been made and must be a value between 0 and 1. A study on EFs showed that an average EF, [math]\displaystyle{ d, }[/math] was about [math]\displaystyle{ 0.7 }[/math] . However, individual EFs for the failure modes may be larger or smaller than the average. Therefore, typically about [math]\displaystyle{ 30% }[/math] , i.e. [math]\displaystyle{ 100(1-d)% }[/math] , of the BD mode failure intensity will remain in the system after all of the corrective actions have been implemented.
Similar to the Crow Extended model, each BD mode has an effectiveness factor that represents the decrease in failure intensity for that mode once the corrective action has been incorporated into the system. In addition, a delayed fix can be incorporated any time after the first occurrence of the failure mode. Therefore, delayed fixes can be incorporated before the end of the test phase, at the end of the test phase (just like the Crow Extended delayed fixes) or not incorporated at all at the end of the current test phase but postponed for a subsequent test phase. For calculation purposes, any delayed fixes that are incorporated during the test (those with an I event code) do not need to have an effectiveness factor specified, since the fix is already incorporated in the system. Figure EF shows how effectiveness factors are defined in the Crow Extended - Continuous Evaluation model in RGA 7. The figure also shows that you can specify if the delayed fix was actually implemented at the end of the current test phase, at a later phase or not implemented at all.
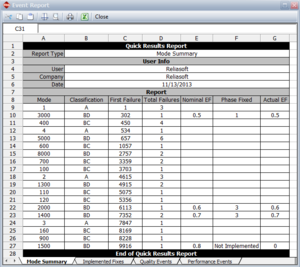
For a Type BD failure mode not yet corrected but still deferred, the Actual Effectiveness Factor for that mode is zero. The Actual Effectiveness Factor for a deferred Type BD failure mode will stay at zero until the point when the corrective action will be incorporated. At that time, the Actual Effectiveness Factor is changed to equal the Assigned Effectiveness Factor for that mode. At this point, the Nominal Effectiveness Factor (the effectiveness factor assuming fixes are implemented at the end of the specific phase) and the Actual Effectiveness Factor are the same. In other words, if a fix is not incorporated for a BD mode, its actual effectiveness for reducing failure intensity is zero, and the assigned effectiveness factor will be used only for projecting the MTBF (or failure intensity), as it will be discussed in Section 10.2.5. Figure Event report shows an event report in RGA 7. At the end of the test phase, depending on whether the BD mode was specified as fixed or not fixed, the actual EF is zero (e.g. mode BD3000) or equal to the nominal EF (e.g. mode BD1500).
[math]\displaystyle{ }[/math]
The Average Nominal EF is:
- [math]\displaystyle{ {{d}_{N}}=\frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} }[/math]
where [math]\displaystyle{ M }[/math] is the total number of open and distinct BD modes at time [math]\displaystyle{ {{T}_{J}} }[/math] and is the Nominal Effectiveness Factor as specified for each of the BD mode.
The Average Actual EF is:
- [math]\displaystyle{ {{d}_{A}}=\frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M} }[/math]
where [math]\displaystyle{ M }[/math] is the total number of open and distinct BD modes at time [math]\displaystyle{ {{T}_{J}} }[/math] and [math]\displaystyle{ {{d}_{{{A}_{i}}}} }[/math] is the Actual Effectiveness Factor at time [math]\displaystyle{ {{T}_{j}} }[/math] for each BD mode.