Template:Graphical method duane
Graphical Method
Eqn. (duaneb) may be linearized by taking the natural log of both sides:
- [math]\displaystyle{ \ln \left( {{\widehat{{\bar{\lambda }}}}_{c}} \right)=\ln \left( \frac{1}{b} \right)-\alpha \ln (T) }[/math]
Consequently, plotting [math]\displaystyle{ \widehat{{\bar{\lambda }}} }[/math] versus [math]\displaystyle{ T }[/math] on log-log paper will result in a straight line with a negative slope, such that:
- [math]\displaystyle{ ln{\frac{1}{b}}=\text{the y-intercept at T}=1 }[/math]
- [math]\displaystyle{ \frac{1}{b}=\text{the cumulative failure intensity at T}=1 }[/math]
- [math]\displaystyle{ \alpha=\text{the slope of the straight line on the log-log plot} }[/math]
Similarly, Eqn. (duane6) can also be linearized by taking the natural log of both sides:
Plotting [math]\displaystyle{ \hat{m} }[/math] versus [math]\displaystyle{ T }[/math] on log-log paper will result in a straight line with a positive slope such that:
- [math]\displaystyle{ \ln{b}=\text{the y-intercept at T}=1 }[/math]
- [math]\displaystyle{ b=\text{the cumulative mean time between failure at T}=1 }[/math]
- [math]\displaystyle{ \alpha=\text{the slope of the straight line on the log-log plot} }[/math]
Two ways of determining these curves are as follows:
- 1.Predict the [math]\displaystyle{ {{\widehat{{\bar{\lambda }}}}_{0}} }[/math] and [math]\displaystyle{ \hat{m}= }[/math] [math]\displaystyle{ \tfrac{1}{{{\widehat{{\bar{\lambda }}}}_{0}}} }[/math] of the system from its reliability block diagram and available component failure intensities. Plot this value on log-log plotting paper at [math]\displaystyle{ T=1. }[/math] From past experience and from past data for similar equipment, find values of [math]\displaystyle{ {{\alpha }_{1}} }[/math] , the slope of the improvement lines for [math]\displaystyle{ \widehat{{\bar{\lambda }}} }[/math] or [math]\displaystyle{ \hat{m} }[/math] . Modify this [math]\displaystyle{ \alpha }[/math] as necessary. If a better design effort is expected and a more intensive research, test and development or TAAF program is to be implemented, then a [math]\displaystyle{ 15% }[/math] improvement in the growth rate may be attainable. Consequently, the available value for slope [math]\displaystyle{ \alpha }[/math] , and [math]\displaystyle{ {{\alpha }_{1}} }[/math] , should be adjusted by this amount. The value to be used will then be [math]\displaystyle{ \alpha =1.15{{\alpha }_{1}}. }[/math] A line is then drawn through point [math]\displaystyle{ {{\widehat{{\bar{\lambda }}}}_{0}} }[/math] and [math]\displaystyle{ T=1 }[/math] with the just determined slope [math]\displaystyle{ \alpha }[/math] , keeping in mind that [math]\displaystyle{ \alpha }[/math] is negative for the [math]\displaystyle{ \widehat{{\bar{\lambda }}} }[/math] curve. This line should be extended to the design, development and test time scheduled to be expended to see if the failure intensity goal will indeed be achieved on schedule. It is also possible to find that the design, development and test time to achieve the goal may be earlier than the delivery date or later. If earlier, then either the reliability program effort can be judiciously and appropriately trimmed; or if it is an incentive contract, full advantage is taken of the fact that the failure intensity goal can be exceeded with the associated increased profits to the company. A similar approach may be used for the MTBF growth model, where [math]\displaystyle{ {{\hat{m}}_{0}}=\tfrac{1}{{{\widehat{{\bar{\lambda }}}}_{0}}} }[/math] is plotted at [math]\displaystyle{ T=1 }[/math] , and a line is drawn through the point [math]\displaystyle{ {{\hat{m}}_{0}} }[/math] and [math]\displaystyle{ T=1 }[/math] with slope [math]\displaystyle{ \alpha }[/math] to obtain the MTBF growth line. If [math]\displaystyle{ \alpha }[/math] values are not available, consult Table 4.1, which gives actual [math]\displaystyle{ \alpha }[/math] values for various types of equipment. These have been obtained from the literature or by MTBF growth tests. It may be seen from Table 4.1 that [math]\displaystyle{ \alpha }[/math] values range between 0.24 and 0.65. The lower values reflect slow early growth and the higher values reflect fast early growth.
| Equipment | Slope([math]\displaystyle{ \alpha }[/math]) | |
|---|---|---|
| Computer system | Actual | 0.24 |
| Easy to find failures were eliminated | 0.26 | |
| All known failure causes were eliminated | 0.36 | |
| Mainframe computer | 0.50 | |
| Aerospace electronics | All malfunctions | 0.57 |
| Relevant failures only | 0.65 | |
| Attack radar | 0.60 | |
| Rocket engine | 0.46 | |
| Afterburning turbojet | 0.35 | |
| Complex hydromechanical system | 0.60 | |
| Aircraft generator | 0.38 | |
| Modern dry turbojet | 0.48 |
- 2) During the design, development and test phase and at specific milestones, the [math]\displaystyle{ \widehat{{\bar{\lambda }}}=\tfrac{1}{{\hat{m}}} }[/math] is calculated from the total failures and [math]\displaystyle{ T }[/math] values. These values of [math]\displaystyle{ \widehat{{\bar{\lambda }}} }[/math] or [math]\displaystyle{ \hat{m} }[/math] are plotted above the corresponding [math]\displaystyle{ T }[/math] values on log-log paper. A straight line is drawn favoring these points to minimize the distance between the points and the line, thus establishing the improvement or growth model and its parameters graphically. If needed, linear regression analysis techniques can be used to determine these parameters.
Example 1
A complex system's reliability growth is being monitored and the data set is given in Table 4.2.
Do the following:
- 1) Plot the cumulative MTBF growth curve.
- 2) Write the equation of this growth curve.
- 3) Write the equation of the instantaneous MTBF growth model.
- 4) Plot the instantaneous MTBF growth curve.
| Point Number | Cumulative Test Time(hr) | Cumulative Failures | Cumulative MTBF(hr) | Instantaneous MTBF(hr) |
|---|---|---|---|---|
| 1 | 200 | 2 | 100.0 | 100 |
| 2 | 400 | 3 | 133.0 | 200 |
| 3 | 600 | 4 | 150.0 | 200 |
| 4 | 3,000 | 11 | 273.0 | 342.8 |
Solution
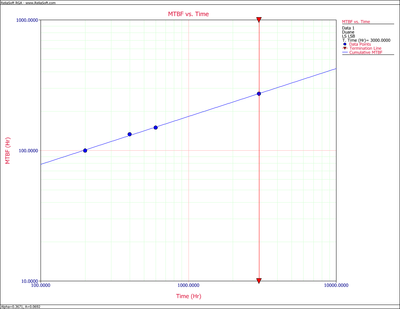
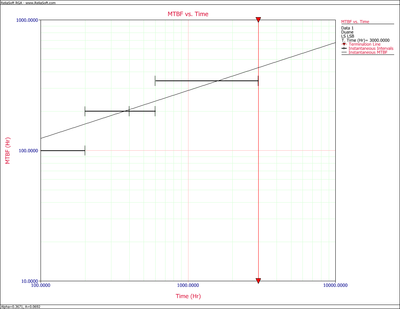
- 1) Given the data in the second and third columns of Table 4.2, the cumulative MTBF, [math]\displaystyle{ {{\hat{m}}_{c}} }[/math] , values are calculated in the fourth column. The information in the second and fourth columns is then plotted. Figure figold72 shows the cumulative MTBF while Figure figold72a shows the instantaneous MTBF. It can be seen that a straight line represents the MTBF growth very well on log-log scales.
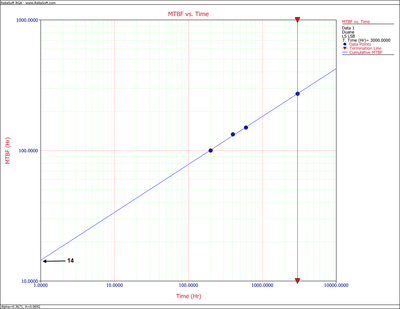
By changing the x-axis scaling, you are able to extend the line to [math]\displaystyle{ T=1 }[/math] . You can get the value of [math]\displaystyle{ b }[/math] from the graph by positioning the cursor at the point where the line meets the y-axis. Then read the value of the y-coordinate position at the bottom left corner. In this case, [math]\displaystyle{ b }[/math] is approximately [math]\displaystyle{ 14 }[/math] hr. Figure figold73 illustrates this.
Another way of determining [math]\displaystyle{ b }[/math] is to calculate [math]\displaystyle{ \alpha }[/math] by using two points on the fitted straight line and substituting the corresponding [math]\displaystyle{ {{\hat{m}}_{c}} }[/math] and [math]\displaystyle{ T }[/math] values into:
- [math]\displaystyle{ \alpha =\frac{\ln \left( {{{\hat{m}}}_{{{c}_{2}}}} \right)-\ln \left( {{{\hat{m}}}_{{{c}_{1}}}} \right)}{\ln \left( {{T}_{_{2}}} \right)-\ln \left( {{T}_{_{1}}} \right)} }[/math]
Then substitute this [math]\displaystyle{ \alpha }[/math] and choose a set of values for [math]\displaystyle{ {{\hat{m}}_{{{c}_{1}}}} }[/math] and [math]\displaystyle{ {{T}_{_{1}}} }[/math] into Eqn. (duane6) and solve for [math]\displaystyle{ b }[/math] . The slope of the line, [math]\displaystyle{ \alpha }[/math] , may also be found from Eqn. (eq73) or from:
- [math]\displaystyle{ \alpha =\frac{\ln \left( {{{\hat{m}}}_{c}} \right)-\ln (b)}{\ln (T)-\ln (1)} }[/math]
Using the plot in Figure figold72, at [math]\displaystyle{ {{T}_{_{1}}}=200 }[/math] hr, [math]\displaystyle{ {{\hat{m}}_{{{c}_{1}}}}=100 }[/math] hr. At [math]\displaystyle{ {{T}_{_{2}}}=3,500 }[/math] hr, [math]\displaystyle{ {{\hat{m}}_{{{c}_{2}}}}=300 }[/math] hr. From Figure figold73, at [math]\displaystyle{ b=14 }[/math] hr when [math]\displaystyle{ T=1 }[/math] .
Substituting the first set of values, [math]\displaystyle{ b=14 }[/math] hr and [math]\displaystyle{ \ln 1=0 }[/math] , into Eqn. (eq77) yields:
- [math]\displaystyle{ \begin{align} & {{\alpha }_{1}}= & \frac{\ln (100)-\ln (14)}{\ln (200)-\ln (1)} \\ & = & 0.3711 \end{align} }[/math]
- 2. Substituting the second set of values, [math]\displaystyle{ b=14 }[/math] hr and [math]\displaystyle{ \ln 1=0, }[/math] into Eqn. (eq77) yields:
- [math]\displaystyle{ \begin{align} & {{\alpha }_{2}}= & \frac{\ln (300)-\ln (14)}{\ln (3,500)-\ln (1)} \\ & = & 0.3755 \end{align} }[/math]
Averaging these two [math]\displaystyle{ \alpha }[/math] values yields a better estimate of [math]\displaystyle{ \widehat{\alpha }=0.3733 }[/math] .
- 3. Now the equation for the cumulative MTBF growth curve is:
[math]\displaystyle{ {{\hat{m}}_{c}}=14\cdot {{T}^{\text{ }0.3733}} }[/math]
- 4. The equation for the instantaneous MTBF growth curve using Eqn. (eq76) is:
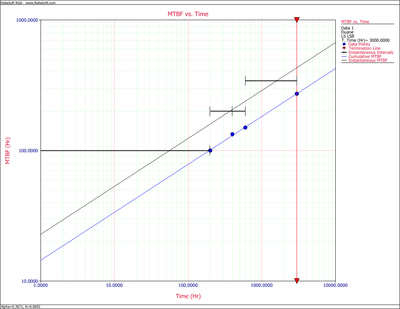
Eqn. (eq80) is plotted in Figures figold72a and figold72b. In Figure figold72b, you can see that a parallel shift upward of the cumulative MTBF, [math]\displaystyle{ {{\hat{m}}_{c}} }[/math] , line by a distance of [math]\displaystyle{ \tfrac{1}{1-\alpha } }[/math] gives the instantaneous MTBF, or the [math]\displaystyle{ {{\hat{m}}_{i}} }[/math] , line.