Template:Maximum likelihood estimators camsaa-cd
Maximum Likelihood Estimators
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Example 8
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
• Configuration 1 experienced 5 failures,
• Configuration 2 experienced 3 failures,
• Configuration 3 experienced 4 failures and
• Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of Eqns. (solution1) and (solution2) provides for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] corresponding to 0.5954 and 0.7801, respectively.
- 2) Table 5.6 displays the results of Eqns. (ffffi) and (rrrri).
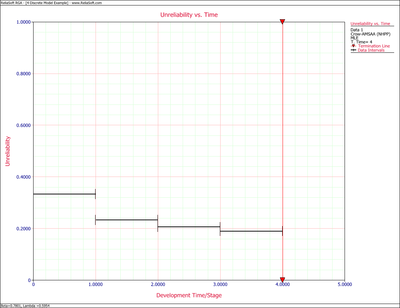
Figures 4fig816 and 4fig817 show plots of the estimated unreliability and reliability by configuration.
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |