Crow-AMSAA (NHPP)
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Parameter Estimation
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Parameter Estimation
Template loop detected: Template:Maximum likelihood estimators camsaa-pe
Template loop detected: Template:Biasing and unbiasing of beta camsaa
Template loop detected: Template:Confidence bounds camsaa
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If Eqn. (amsaa2a) is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Example 4
Consider the grouped failure times data given in Table 5.2. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Template loop detected: Template:Grouped data confidence bounds camsaa
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Template loop detected: Template:Cramer-con mises test for individual failure times
Template loop detected: Template:Chi-squared test for grouped data
Template loop detected: Template:Estimation and analysis with missing data camsaa
Template loop detected: Template:Crow discrete reliability growth model camsaa
Template loop detected: Template:Applicability camsaa
Change of Slope
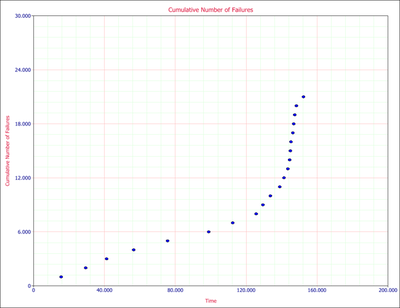
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
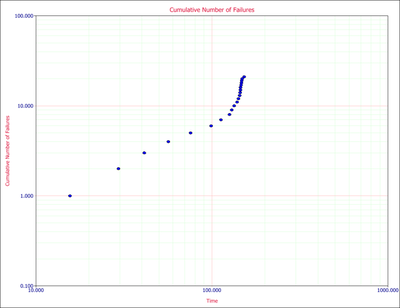
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
• [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
• [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
• [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment (Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
• [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
• [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
• [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Example 10
Table 5.8 - Failure times from a reliability growth test
The test has a duration of 660 hours.
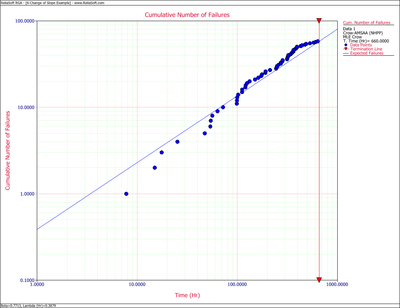
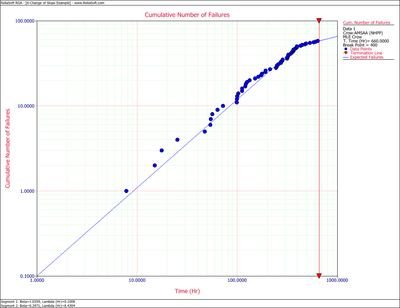
First, apply a single Crow-AMSAA (NHPP) model to all of the data. Figure Changeflopeingleodel shows the expected failures obtained from the model (the line) along with the observed failures (the points).
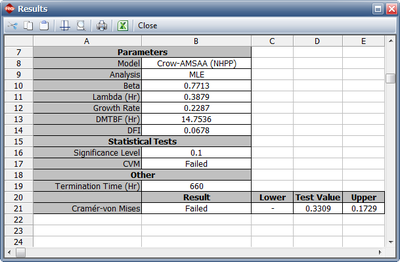
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. Figure Changeflopeingleodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
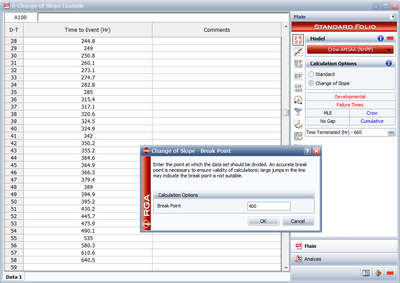
In RGA 7 you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in Figure changeflopereakoint. RGA 7 actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
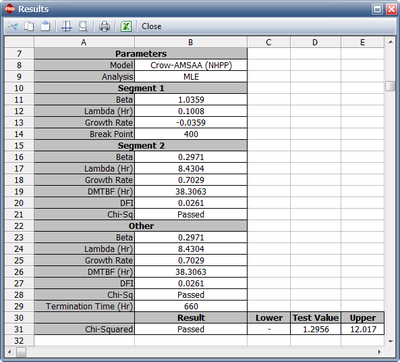
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). Based on Eqns. (lambda1) and (beta1mallq), the Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
Based on Eqns. (lambda2) and (beta2mallq), the Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
Figure changeflopelot shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. Figure Changeflopereakodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
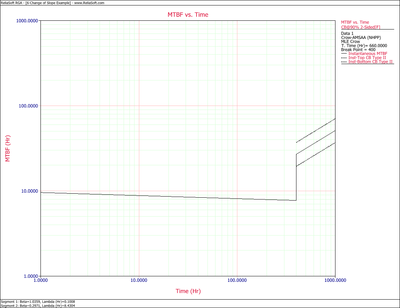
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, Figure changeflopeTBF shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
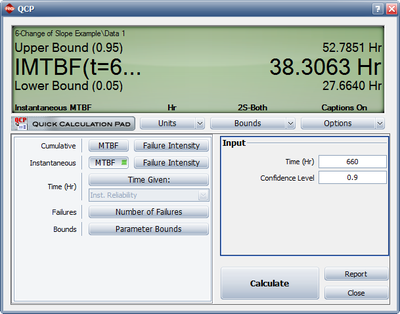
Figure ChangeflopeCP shows the use of the Quick Calculation Pad (QCP) in RGA 7 to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
General Examples
Example 11
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. Table 5.9 presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution to Example 11
- 1) Figure ex9a shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown in Figure ex9b. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
[math]\displaystyle{ }[/math]
Example 12
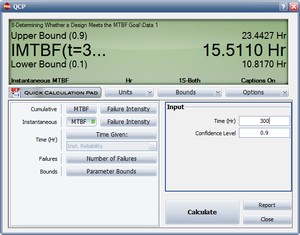
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. Table 5.10 shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution to Example 12
- 1) Figure ex10a shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the
Quick Calculation Pad (QCP) as shown in Figure ex10b. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal. [math]\displaystyle{ }[/math]
Example 13
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. Table 5.11 shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution to Example 13
- 1) Figure Mixedolio shows the parameters estimated using RGA.
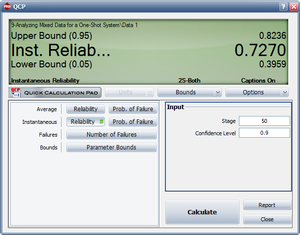
- 2) Figure MixedCP shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
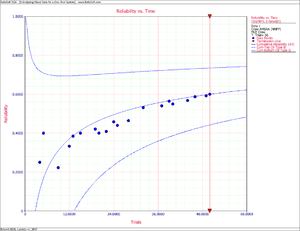
- 3) Figure Mixedeliabilitylot shows the plot of the cumulative reliability with the 2-sided 90% confidence bounds.
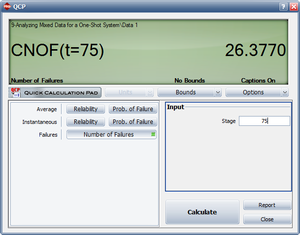
- 4) Figure MixedCPumFailures shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Parameter Estimation
Template loop detected: Template:Maximum likelihood estimators camsaa-pe
Template loop detected: Template:Biasing and unbiasing of beta camsaa
Template loop detected: Template:Confidence bounds camsaa
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If Eqn. (amsaa2a) is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Example 4
Consider the grouped failure times data given in Table 5.2. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Template loop detected: Template:Grouped data confidence bounds camsaa
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Template loop detected: Template:Cramer-con mises test for individual failure times
Template loop detected: Template:Chi-squared test for grouped data
Template loop detected: Template:Estimation and analysis with missing data camsaa
Template loop detected: Template:Crow discrete reliability growth model camsaa
Template loop detected: Template:Applicability camsaa
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
• [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
• [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
• [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment (Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
• [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
• [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
• [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Example 10
Table 5.8 - Failure times from a reliability growth test
The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. Figure Changeflopeingleodel shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. Figure Changeflopeingleodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In RGA 7 you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in Figure changeflopereakoint. RGA 7 actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). Based on Eqns. (lambda1) and (beta1mallq), the Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
Based on Eqns. (lambda2) and (beta2mallq), the Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
Figure changeflopelot shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. Figure Changeflopereakodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, Figure changeflopeTBF shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
Figure ChangeflopeCP shows the use of the Quick Calculation Pad (QCP) in RGA 7 to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
General Examples
Example 11
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. Table 5.9 presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution to Example 11
- 1) Figure ex9a shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown in Figure ex9b. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
[math]\displaystyle{ }[/math]
Example 12
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. Table 5.10 shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution to Example 12
- 1) Figure ex10a shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the
Quick Calculation Pad (QCP) as shown in Figure ex10b. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal. [math]\displaystyle{ }[/math]
Example 13
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. Table 5.11 shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution to Example 13
- 1) Figure Mixedolio shows the parameters estimated using RGA.
- 2) Figure MixedCP shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) Figure Mixedeliabilitylot shows the plot of the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) Figure MixedCPumFailures shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Parameter Estimation
Template loop detected: Template:Maximum likelihood estimators camsaa-pe
Template loop detected: Template:Biasing and unbiasing of beta camsaa
Template loop detected: Template:Confidence bounds camsaa
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If Eqn. (amsaa2a) is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Example 4
Consider the grouped failure times data given in Table 5.2. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Template loop detected: Template:Grouped data confidence bounds camsaa
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Template loop detected: Template:Cramer-con mises test for individual failure times
Template loop detected: Template:Chi-squared test for grouped data
Template loop detected: Template:Estimation and analysis with missing data camsaa
Template loop detected: Template:Crow discrete reliability growth model camsaa
Template loop detected: Template:Applicability camsaa
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
• [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
• [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
• [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment (Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
• [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
• [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
• [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Example 10
Table 5.8 - Failure times from a reliability growth test
The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. Figure Changeflopeingleodel shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. Figure Changeflopeingleodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In RGA 7 you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in Figure changeflopereakoint. RGA 7 actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). Based on Eqns. (lambda1) and (beta1mallq), the Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
Based on Eqns. (lambda2) and (beta2mallq), the Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
Figure changeflopelot shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. Figure Changeflopereakodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, Figure changeflopeTBF shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
Figure ChangeflopeCP shows the use of the Quick Calculation Pad (QCP) in RGA 7 to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
General Examples
Example 11
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. Table 5.9 presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution to Example 11
- 1) Figure ex9a shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown in Figure ex9b. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
[math]\displaystyle{ }[/math]
Example 12
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. Table 5.10 shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution to Example 12
- 1) Figure ex10a shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the
Quick Calculation Pad (QCP) as shown in Figure ex10b. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal. [math]\displaystyle{ }[/math]
Example 13
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. Table 5.11 shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution to Example 13
- 1) Figure Mixedolio shows the parameters estimated using RGA.
- 2) Figure MixedCP shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) Figure Mixedeliabilitylot shows the plot of the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) Figure MixedCPumFailures shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If Eqn. (amsaa2a) is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Example 4
Consider the grouped failure times data given in Table 5.2. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Parameter Estimation
Template loop detected: Template:Maximum likelihood estimators camsaa-pe
Template loop detected: Template:Biasing and unbiasing of beta camsaa
Template loop detected: Template:Confidence bounds camsaa
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If Eqn. (amsaa2a) is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Example 4
Consider the grouped failure times data given in Table 5.2. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Template loop detected: Template:Grouped data confidence bounds camsaa
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Template loop detected: Template:Cramer-con mises test for individual failure times
Template loop detected: Template:Chi-squared test for grouped data
Template loop detected: Template:Estimation and analysis with missing data camsaa
Template loop detected: Template:Crow discrete reliability growth model camsaa
Template loop detected: Template:Applicability camsaa
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
• [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
• [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
• [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment (Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
• [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
• [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
• [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Example 10
Table 5.8 - Failure times from a reliability growth test
The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. Figure Changeflopeingleodel shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. Figure Changeflopeingleodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In RGA 7 you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in Figure changeflopereakoint. RGA 7 actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). Based on Eqns. (lambda1) and (beta1mallq), the Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
Based on Eqns. (lambda2) and (beta2mallq), the Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
Figure changeflopelot shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. Figure Changeflopereakodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, Figure changeflopeTBF shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
Figure ChangeflopeCP shows the use of the Quick Calculation Pad (QCP) in RGA 7 to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
General Examples
Example 11
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. Table 5.9 presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution to Example 11
- 1) Figure ex9a shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown in Figure ex9b. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
[math]\displaystyle{ }[/math]
Example 12
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. Table 5.10 shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution to Example 12
- 1) Figure ex10a shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the
Quick Calculation Pad (QCP) as shown in Figure ex10b. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal. [math]\displaystyle{ }[/math]
Example 13
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. Table 5.11 shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution to Example 13
- 1) Figure Mixedolio shows the parameters estimated using RGA.
- 2) Figure MixedCP shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) Figure Mixedeliabilitylot shows the plot of the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) Figure MixedCPumFailures shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Parameter Estimation
Template loop detected: Template:Maximum likelihood estimators camsaa-pe
Template loop detected: Template:Biasing and unbiasing of beta camsaa
Template loop detected: Template:Confidence bounds camsaa
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If Eqn. (amsaa2a) is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Example 4
Consider the grouped failure times data given in Table 5.2. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Template loop detected: Template:Grouped data confidence bounds camsaa
Template loop detected: Template:Goodness-of-fit test camsaa
Template loop detected: Template:Estimation and analysis with missing data camsaa
Template loop detected: Template:Crow discrete reliability growth model camsaa
Template loop detected: Template:Applicability camsaa
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
• [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
• [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
• [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment (Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
• [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
• [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
• [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Example 10
Table 5.8 - Failure times from a reliability growth test
The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. Figure Changeflopeingleodel shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. Figure Changeflopeingleodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In RGA 7 you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in Figure changeflopereakoint. RGA 7 actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). Based on Eqns. (lambda1) and (beta1mallq), the Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
Based on Eqns. (lambda2) and (beta2mallq), the Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
Figure changeflopelot shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. Figure Changeflopereakodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, Figure changeflopeTBF shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
Figure ChangeflopeCP shows the use of the Quick Calculation Pad (QCP) in RGA 7 to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
General Examples
Example 11
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. Table 5.9 presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution to Example 11
- 1) Figure ex9a shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown in Figure ex9b. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
[math]\displaystyle{ }[/math]
Example 12
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. Table 5.10 shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution to Example 12
- 1) Figure ex10a shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the
Quick Calculation Pad (QCP) as shown in Figure ex10b. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal. [math]\displaystyle{ }[/math]
Example 13
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. Table 5.11 shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution to Example 13
- 1) Figure Mixedolio shows the parameters estimated using RGA.
- 2) Figure MixedCP shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) Figure Mixedeliabilitylot shows the plot of the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) Figure MixedCPumFailures shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Parameter Estimation
Template loop detected: Template:Maximum likelihood estimators camsaa-pe
Template loop detected: Template:Biasing and unbiasing of beta camsaa
Template loop detected: Template:Confidence bounds camsaa
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If Eqn. (amsaa2a) is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Example 4
Consider the grouped failure times data given in Table 5.2. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Template loop detected: Template:Grouped data confidence bounds camsaa
Template loop detected: Template:Goodness-of-fit test camsaa
Template loop detected: Template:Estimation and analysis with missing data camsaa
Template loop detected: Template:Crow discrete reliability growth model camsaa
Template loop detected: Template:Applicability camsaa
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
• [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
• [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
• [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment (Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
• [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
• [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
• [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Example 10
Table 5.8 - Failure times from a reliability growth test
The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. Figure Changeflopeingleodel shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. Figure Changeflopeingleodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In RGA 7 you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in Figure changeflopereakoint. RGA 7 actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). Based on Eqns. (lambda1) and (beta1mallq), the Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
Based on Eqns. (lambda2) and (beta2mallq), the Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
Figure changeflopelot shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. Figure Changeflopereakodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, Figure changeflopeTBF shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
Figure ChangeflopeCP shows the use of the Quick Calculation Pad (QCP) in RGA 7 to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
General Examples
Example 11
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. Table 5.9 presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution to Example 11
- 1) Figure ex9a shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown in Figure ex9b. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
[math]\displaystyle{ }[/math]
Example 12
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. Table 5.10 shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution to Example 12
- 1) Figure ex10a shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the
Quick Calculation Pad (QCP) as shown in Figure ex10b. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal. [math]\displaystyle{ }[/math]
Example 13
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. Table 5.11 shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution to Example 13
- 1) Figure Mixedolio shows the parameters estimated using RGA.
- 2) Figure MixedCP shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) Figure Mixedeliabilitylot shows the plot of the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) Figure MixedCPumFailures shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Parameter Estimation
Template loop detected: Template:Maximum likelihood estimators camsaa-pe
Template loop detected: Template:Biasing and unbiasing of beta camsaa
Template loop detected: Template:Confidence bounds camsaa
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If Eqn. (amsaa2a) is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Example 4
Consider the grouped failure times data given in Table 5.2. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Template loop detected: Template:Grouped data confidence bounds camsaa
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Template loop detected: Template:Cramer-con mises test for individual failure times
Template loop detected: Template:Chi-squared test for grouped data
Template loop detected: Template:Estimation and analysis with missing data camsaa
Template loop detected: Template:Crow discrete reliability growth model camsaa
Template loop detected: Template:Applicability camsaa
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
• [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
• [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
• [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment (Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
• [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
• [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
• [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Example 10
Table 5.8 - Failure times from a reliability growth test
The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. Figure Changeflopeingleodel shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. Figure Changeflopeingleodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In RGA 7 you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in Figure changeflopereakoint. RGA 7 actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). Based on Eqns. (lambda1) and (beta1mallq), the Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
Based on Eqns. (lambda2) and (beta2mallq), the Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
Figure changeflopelot shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. Figure Changeflopereakodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, Figure changeflopeTBF shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
Figure ChangeflopeCP shows the use of the Quick Calculation Pad (QCP) in RGA 7 to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
General Examples
Example 11
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. Table 5.9 presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution to Example 11
- 1) Figure ex9a shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown in Figure ex9b. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
[math]\displaystyle{ }[/math]
Example 12
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. Table 5.10 shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution to Example 12
- 1) Figure ex10a shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the
Quick Calculation Pad (QCP) as shown in Figure ex10b. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal. [math]\displaystyle{ }[/math]
Example 13
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. Table 5.11 shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution to Example 13
- 1) Figure Mixedolio shows the parameters estimated using RGA.
- 2) Figure MixedCP shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) Figure Mixedeliabilitylot shows the plot of the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) Figure MixedCPumFailures shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Parameter Estimation
Template loop detected: Template:Maximum likelihood estimators camsaa-pe
Template loop detected: Template:Biasing and unbiasing of beta camsaa
Template loop detected: Template:Confidence bounds camsaa
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If Eqn. (amsaa2a) is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Example 4
Consider the grouped failure times data given in Table 5.2. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Template loop detected: Template:Grouped data confidence bounds camsaa
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Template loop detected: Template:Cramer-con mises test for individual failure times
Template loop detected: Template:Chi-squared test for grouped data
Template loop detected: Template:Estimation and analysis with missing data camsaa
Template loop detected: Template:Crow discrete reliability growth model camsaa
Template loop detected: Template:Applicability camsaa
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
• [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
• [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
• [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment (Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
• [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
• [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
• [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Example 10
Table 5.8 - Failure times from a reliability growth test
The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. Figure Changeflopeingleodel shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. Figure Changeflopeingleodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In RGA 7 you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in Figure changeflopereakoint. RGA 7 actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). Based on Eqns. (lambda1) and (beta1mallq), the Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
Based on Eqns. (lambda2) and (beta2mallq), the Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
Figure changeflopelot shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. Figure Changeflopereakodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, Figure changeflopeTBF shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
Figure ChangeflopeCP shows the use of the Quick Calculation Pad (QCP) in RGA 7 to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
General Examples
Example 11
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. Table 5.9 presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution to Example 11
- 1) Figure ex9a shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown in Figure ex9b. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
[math]\displaystyle{ }[/math]
Example 12
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. Table 5.10 shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution to Example 12
- 1) Figure ex10a shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the
Quick Calculation Pad (QCP) as shown in Figure ex10b. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal. [math]\displaystyle{ }[/math]
Example 13
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. Table 5.11 shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution to Example 13
- 1) Figure Mixedolio shows the parameters estimated using RGA.
- 2) Figure MixedCP shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) Figure Mixedeliabilitylot shows the plot of the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) Figure MixedCPumFailures shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Parameter Estimation
Template loop detected: Template:Maximum likelihood estimators camsaa-pe
Template loop detected: Template:Biasing and unbiasing of beta camsaa
Template loop detected: Template:Confidence bounds camsaa
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If Eqn. (amsaa2a) is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Example 4
Consider the grouped failure times data given in Table 5.2. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Template loop detected: Template:Grouped data confidence bounds camsaa
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Template loop detected: Template:Cramer-con mises test for individual failure times
Template loop detected: Template:Chi-squared test for grouped data
Template loop detected: Template:Estimation and analysis with missing data camsaa
Template loop detected: Template:Crow discrete reliability growth model camsaa
Template loop detected: Template:Applicability camsaa
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
• [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
• [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
• [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment (Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
• [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
• [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
• [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Example 10
Table 5.8 - Failure times from a reliability growth test
The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. Figure Changeflopeingleodel shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. Figure Changeflopeingleodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In RGA 7 you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in Figure changeflopereakoint. RGA 7 actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). Based on Eqns. (lambda1) and (beta1mallq), the Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
Based on Eqns. (lambda2) and (beta2mallq), the Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
Figure changeflopelot shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. Figure Changeflopereakodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, Figure changeflopeTBF shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
Figure ChangeflopeCP shows the use of the Quick Calculation Pad (QCP) in RGA 7 to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
General Examples
Example 11
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. Table 5.9 presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution to Example 11
- 1) Figure ex9a shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown in Figure ex9b. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
[math]\displaystyle{ }[/math]
Example 12
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. Table 5.10 shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution to Example 12
- 1) Figure ex10a shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the
Quick Calculation Pad (QCP) as shown in Figure ex10b. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal. [math]\displaystyle{ }[/math]
Example 13
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. Table 5.11 shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution to Example 13
- 1) Figure Mixedolio shows the parameters estimated using RGA.
- 2) Figure MixedCP shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) Figure Mixedeliabilitylot shows the plot of the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) Figure MixedCPumFailures shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
• [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
• [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
• [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment (Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
• [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
• [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
• [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Example 10
Table 5.8 - Failure times from a reliability growth test
The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. Figure Changeflopeingleodel shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. Figure Changeflopeingleodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In RGA 7 you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in Figure changeflopereakoint. RGA 7 actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). Based on Eqns. (lambda1) and (beta1mallq), the Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
Based on Eqns. (lambda2) and (beta2mallq), the Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
Figure changeflopelot shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. Figure Changeflopereakodelesults shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, Figure changeflopeTBF shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
Figure ChangeflopeCP shows the use of the Quick Calculation Pad (QCP) in RGA 7 to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
General Examples
Example 11
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. Table 5.9 presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution to Example 11
- 1) Figure ex9a shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown in Figure ex9b. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
[math]\displaystyle{ }[/math]
Example 12
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. Table 5.10 shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution to Example 12
- 1) Figure ex10a shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the
Quick Calculation Pad (QCP) as shown in Figure ex10b. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal. [math]\displaystyle{ }[/math]
Example 13
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. Table 5.11 shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution to Example 13
- 1) Figure Mixedolio shows the parameters estimated using RGA.
- 2) Figure MixedCP shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) Figure Mixedeliabilitylot shows the plot of the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) Figure MixedCPumFailures shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.