Optimum Replacement Time Example

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at BlockSim examples and BlockSim reference examples.

---

This example appears in the System Analysis Reference book.

This example demonstrates BlockSim 8's Optimum Replacement utility, which allows you to determine the most cost-effective time to replace one or more blocks in one or more systems, based on their planned and unplanned replacement costs.

Optimum Replacement Time

The failure distribution of a component is described by a 2-parameter Weibull distribution with [math]\displaystyle{ \beta = 2.5\,\! }[/math] and [math]\displaystyle{ \eta = 1000\,\! }[/math] hours.

• The cost for a corrective replacement is $5.
  
• The cost for a preventive replacement is $1.
  

Estimate the optimum replacement age in order to minimize these costs.

Solution

Prior to obtaining an optimum replacement interval for this component, the assumptions of the following equation must be checked.

[math]\displaystyle{ \begin{align} CPUT\left( t \right)= & \frac{\text{Total Expected Replacement Cost per Cycle}}{\text{Expected Cycle Length}} \\ = & \frac{{{C}_{P}}\cdot R\left( t \right)+{{C}_{U}}\cdot \left[ 1-R\left( t \right) \right]}{\mathop{}_{0}^{t}R\left( s \right)ds} \end{align} }[/math]

The component has an increasing failure rate because it follows a Weibull distribution with [math]\displaystyle{ \beta \,\! }[/math] greater than 1. Note that if [math]\displaystyle{ \beta =1\,\! }[/math], then the component has a constant failure rate, but if [math]\displaystyle{ \beta \lt 1\,\! }[/math], then it has a decreasing failure rate. If either of these cases exist, then preventive replacement is unwise. Furthermore, the cost for preventive replacement is less than the corrective replacement cost. Thus, the conditions for the optimum age replacement policy have been met.

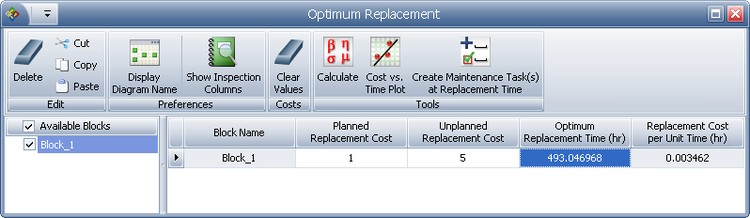
Using BlockSim 8, enter the parameters of the Weibull distribution in the component's Block Properties window. Next, open the Optimum Replacement window and enter the $1 in the Additional Planned Replacement Cost column, and $5 in the Additional Unplanned Replacement Cost column. Click Calculate. In the Optimum Replacement Calculations window that appears, select the Calculate the individual optimum replacement times option and click OK. The optimum replacement time for the component is estimated to be [math]\displaystyle{ 493.0470 }[/math], as shown next.

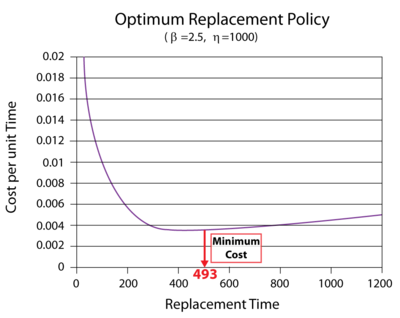
The figure below shows the Cost vs. Time plot of the component (with the scaling adjusted and the plot annotated to show the minimum cost).

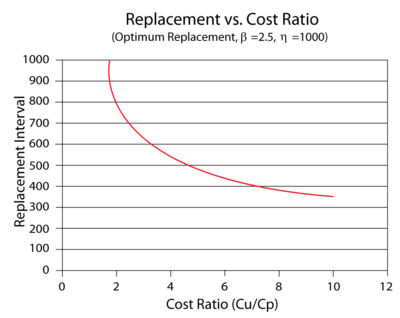
The effect of the corrective/preventive cost ratio on the optimum replacement interval is plotted in the following figure. It can be seen that as the cost ratio increases, the optimum replacement interval decreases. This is an expected result because the corrective replacement costs are much greater than the preventive replacement costs. Therefore, it becomes more cost-effective to replace the component more frequently before it fails.

BlockSim 8 Optimum Replacement Window

---

In BlockSim 7, the optimum replacement calculations were performed for individual blocks. In Version 8, you can now perform calculations either for an individual block or for multiple blocks in a diagram simultaneously. When working with multiple blocks, the calculations can be for individual blocks or for one or more groups of blocks.

If you are working with a diagram instead of with a single block, the Available Blocks area on the left side of the window lists all of the standard blocks (in RBDs) or the events (in fault trees), as well as the switches for any standby containers. You can select an individual item's check box or drag the block into the table on the right side of the window to include the item in the optimization calculations. You can also select the check box in the Available Blocks header to select all check boxes. To remove items from the optimization calculations, you must clear the check box(es); you cannot drag items out of the table.

The following requirements must be met for an item to be available for inclusion in the optimization calculations:

• Blocks must have a failure distribution.

• Switches must have a failure model assigned. Note that in the standby configuration, the switch is the item that is optimized, not the container or the contained blocks/dependent events.

The failure model must meet the following requirements.

• Fixed reliability and exponential distributions are not allowed.

• Weibull distributions must have beta > 1.

• Gamma distributions must have k > 1.

• Loglogistic distributions must have std < 1.

• For generalized gamma distributions and mixed Weibull distributions, there must be an increasing failure rate within at least one time period. A local optimum can then be found within intervals with an increasing failure rate.

For each item that is included in the optimization calculations, you will need to specify the cost for a planned replacement and the cost for an unplanned replacement. This is done by calculating the costs for replacement based on the item settings using equations or simulation and then, if desired, manually entering any additional costs for either type of replacement in the corresponding columns of the table.

Optimum Replacement Calculations

• Estimate Costs calculates the costs of planned and unplanned tasks for each item based on its associated URD using the following equations.

• For the cost of planned tasks, here denoted as PM cost:

[math]\displaystyle{ \begin{align} \text{PM Cost}= \left(\text{PM Down Time Rate}+ \text{Block Level Down Time Rate} \right)\cdot \left( \text{MTTPM}+\text{Pool Delay} +\text{Crew Delay} \right) \\ + \text{Crew Labor Rate} \cdot \text{MTTPM} + \text{Cost per PM} + \text{Cost per Pool} +\text{Cost per Crew} \end{align} }[/math]

Notice: Only PM tasks based on item age are considered. If there is more than one PM task based on item age, only the first one is considered.

• For the cost of the unplanned task, here denoted as CM cost:

[math]\displaystyle{ \begin{align} \text{CM Cost}= \left(\text{CM Down Time Rate}+ \text{Block Level Down Time Rate} \right)\cdot \left( \text{MTTR}+\text{Pool Delay} +\text{Crew Delay} \right) \\ + \text{Crew Labor Rate} \cdot \text{MTTR} + \text{Cost per CM} + \text{Cost per Pool} +\text{Cost per Crew} \\ +\text{Block Level Cost per Failure} \end{align} }[/math]

The results will be used to populate the Calculated Planned Replacement Cost and Calculated Unplanned Replacement Cost columns.

• Estimate Costs Using Simulation calculates the costs of planned and unplanned tasks for each item based on its associated URD using simulation. In other words, we run simulation for each item alone and estimate its costs. When you choose this command, a Simulation Settings window is shown, allowing you to specify the simulation settings. Once the simulation settings are specified, you can estimate the costs for each item using simulation.

The results will be used to populate the Calculated Planned Replacement Cost and Calculated Unplanned Replacement Cost columns.

• Calculate. If you are working with a diagram instead of with a single block, the Calculate command allows you to choose from the following options:

• Calculate the individual optimum replacement time for each item.
• Calculate a common optimum replacement time, which is the most cost-effective time to replace all of the selected items concurrently.
• Calculate clustered optimum replacement times, which allows you to specify a number of times to replace groups of the selected items. For example, if you enter 3 in the Number of clusters field, the software will determine the three best times to replace groups of items such that all of the selected items are replaced at one of the three times.

If you are working with a single block, no choice is necessary.

BlockSim will calculate the optimum replacement time for the items based on their failure characteristics and on the defined costs. This value will be displayed in the Optimum Replacement Time column of the table. In addition, the Cost per Unit Time column will display the estimated cost per unit time for a replacement performed at the calculated optimum replacement time. Multiply the replacement time by the cost per unit time to obtain the cost of replacing the item at the optimum replacement time.

• Cost vs. Time Plot shows a plot of the results. If you have calculated individual optimum replacement times, the plot will show the cost for each item as a function of time. If you have calculated a common optimum replacement time, the plot will show the common cost as a function of time. If you have calculated clustered optimum replacement times, the plot will show the cost for each cluster as a function of time.

• Create Maintenance Task(s) at Replacement Time is available if you have accessed the Optimum Replacement window from a simulation diagram or a block within a simulation diagram. This command enables you to create a preventive task for one or more of the items. The window that appears allows you to select which items to create tasks for. The preventive tasks created in this way restore the item to as good as new condition and are scheduled at fixed intervals based on item age, equal to the optimum replacement time.