Normal Distribution Examples
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
These examples appear in the Life Data Analysis Reference book book.
The following examples illustrate the different types of life data that can be analyzed in Weibull++ using the Normal distribution.
Complete Data
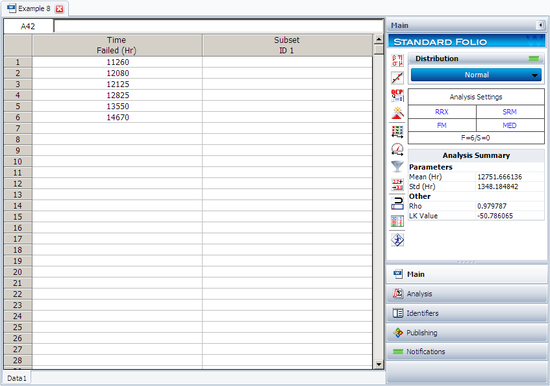
Six units are tested to failure. The following hours-to-failure data are obtained: 12125, 11260, 12080, 12825, 13550 and 14670 hours. Assuming that the data are normally distributed, do the following:
- 1. Find the parameters for the data set, using the Rank Regression on X (RRX) parameter estimation method
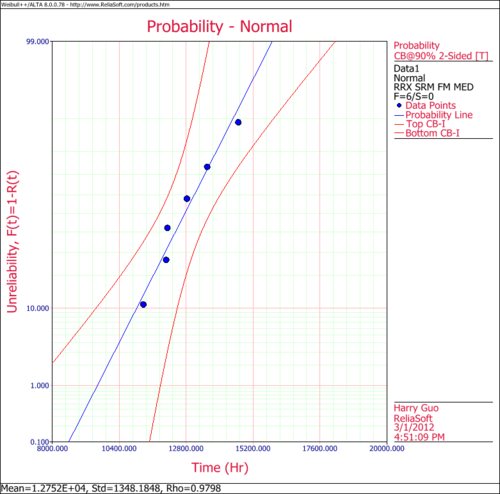
- 2. Obtain the probability plot for the data with 90%, two-sided Type 1 confidence bounds.
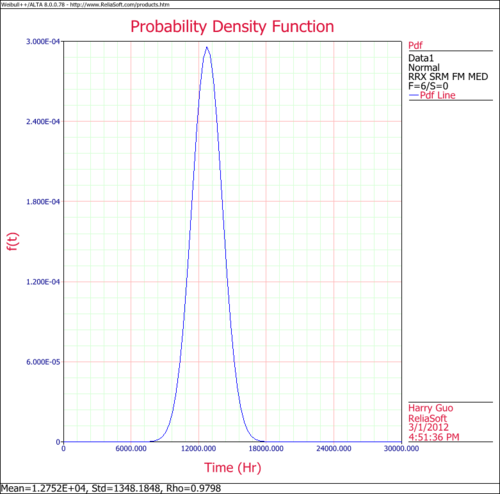
- 3. Obtain the [math]\displaystyle{ pdf }[/math] plot for the data.
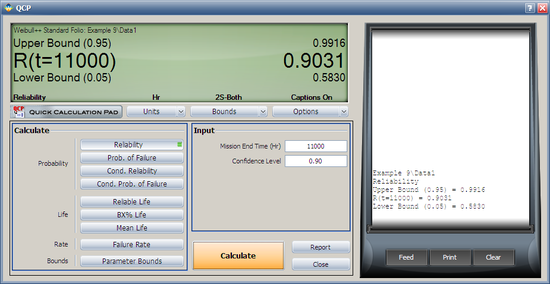
- 4. Using the Quick Calculation Pad, determine the reliability for a mission of 11,000 hours, as well as the upper and lower two-sided 90% confidence limit on this reliability.
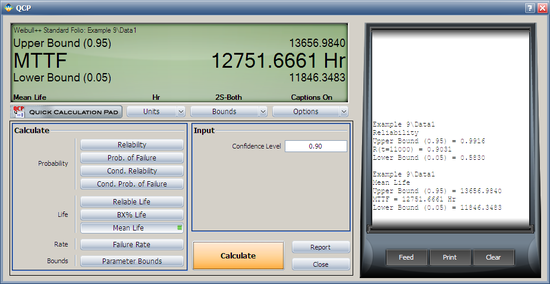
- 5. 2. Using the Quick Calculation Pad, determine the MTTF, as well as the upper and lower two-sided 90% confidence limit on this MTTF.
Solution
The following figure shows the data as entered in Weibull++, as well as the calculated parameters.
The following figures show the probability plot with the 90% two-sided confidence bounds and the pdf plot.
Both the reliability and MTTF can be easily obtained from the QCP. The QCP, with results, for both cases is shown in the next two figures.
Example 3
The following examples illustrate the different types of life data that can be analyzed in Weibull++ using the Normal distribution.
Complete Data
Six units are tested to failure. The following hours-to-failure data are obtained: 12125, 11260, 12080, 12825, 13550 and 14670 hours. Assuming that the data are normally distributed, do the following:
- 1. Find the parameters for the data set, using the Rank Regression on X (RRX) parameter estimation method
- 2. Obtain the probability plot for the data with 90%, two-sided Type 1 confidence bounds.
- 3. Obtain the [math]\displaystyle{ pdf }[/math] plot for the data.
- 4. Using the Quick Calculation Pad, determine the reliability for a mission of 11,000 hours, as well as the upper and lower two-sided 90% confidence limit on this reliability.
- 5. 2. Using the Quick Calculation Pad, determine the MTTF, as well as the upper and lower two-sided 90% confidence limit on this MTTF.
Solution
The following figure shows the data as entered in Weibull++, as well as the calculated parameters.
The following figures show the probability plot with the 90% two-sided confidence bounds and the pdf plot.
Both the reliability and MTTF can be easily obtained from the QCP. The QCP, with results, for both cases is shown in the next two figures.
Example 3
Template loop detected: Template:Example: Normal General Example (RRX Report)
Example 4
Template loop detected: Template:Example: Normal General Example Interval Data
Example 5
Template loop detected: Template:Example: Normal General Example Complete Data
Example 6
Template loop detected: Template:Example: Normal General Example Suspension Data
Example 7
Template loop detected: Template:Example: Normal General Example All Data Type
Example 4
The following examples illustrate the different types of life data that can be analyzed in Weibull++ using the Normal distribution.
Complete Data
Six units are tested to failure. The following hours-to-failure data are obtained: 12125, 11260, 12080, 12825, 13550 and 14670 hours. Assuming that the data are normally distributed, do the following:
- 1. Find the parameters for the data set, using the Rank Regression on X (RRX) parameter estimation method
- 2. Obtain the probability plot for the data with 90%, two-sided Type 1 confidence bounds.
- 3. Obtain the [math]\displaystyle{ pdf }[/math] plot for the data.
- 4. Using the Quick Calculation Pad, determine the reliability for a mission of 11,000 hours, as well as the upper and lower two-sided 90% confidence limit on this reliability.
- 5. 2. Using the Quick Calculation Pad, determine the MTTF, as well as the upper and lower two-sided 90% confidence limit on this MTTF.
Solution
The following figure shows the data as entered in Weibull++, as well as the calculated parameters.
The following figures show the probability plot with the 90% two-sided confidence bounds and the pdf plot.
Both the reliability and MTTF can be easily obtained from the QCP. The QCP, with results, for both cases is shown in the next two figures.
Example 3
Template loop detected: Template:Example: Normal General Example (RRX Report)
Example 4
Template loop detected: Template:Example: Normal General Example Interval Data
Example 5
Template loop detected: Template:Example: Normal General Example Complete Data
Example 6
Template loop detected: Template:Example: Normal General Example Suspension Data
Example 7
Template loop detected: Template:Example: Normal General Example All Data Type
Example 5
The following examples illustrate the different types of life data that can be analyzed in Weibull++ using the Normal distribution.
Complete Data
Six units are tested to failure. The following hours-to-failure data are obtained: 12125, 11260, 12080, 12825, 13550 and 14670 hours. Assuming that the data are normally distributed, do the following:
- 1. Find the parameters for the data set, using the Rank Regression on X (RRX) parameter estimation method
- 2. Obtain the probability plot for the data with 90%, two-sided Type 1 confidence bounds.
- 3. Obtain the [math]\displaystyle{ pdf }[/math] plot for the data.
- 4. Using the Quick Calculation Pad, determine the reliability for a mission of 11,000 hours, as well as the upper and lower two-sided 90% confidence limit on this reliability.
- 5. 2. Using the Quick Calculation Pad, determine the MTTF, as well as the upper and lower two-sided 90% confidence limit on this MTTF.
Solution
The following figure shows the data as entered in Weibull++, as well as the calculated parameters.
The following figures show the probability plot with the 90% two-sided confidence bounds and the pdf plot.
Both the reliability and MTTF can be easily obtained from the QCP. The QCP, with results, for both cases is shown in the next two figures.
Example 3
Template loop detected: Template:Example: Normal General Example (RRX Report)
Example 4
Template loop detected: Template:Example: Normal General Example Interval Data
Example 5
Template loop detected: Template:Example: Normal General Example Complete Data
Example 6
Template loop detected: Template:Example: Normal General Example Suspension Data
Example 7
Template loop detected: Template:Example: Normal General Example All Data Type
Example 6
The following examples illustrate the different types of life data that can be analyzed in Weibull++ using the Normal distribution.
Complete Data
Six units are tested to failure. The following hours-to-failure data are obtained: 12125, 11260, 12080, 12825, 13550 and 14670 hours. Assuming that the data are normally distributed, do the following:
- 1. Find the parameters for the data set, using the Rank Regression on X (RRX) parameter estimation method
- 2. Obtain the probability plot for the data with 90%, two-sided Type 1 confidence bounds.
- 3. Obtain the [math]\displaystyle{ pdf }[/math] plot for the data.
- 4. Using the Quick Calculation Pad, determine the reliability for a mission of 11,000 hours, as well as the upper and lower two-sided 90% confidence limit on this reliability.
- 5. 2. Using the Quick Calculation Pad, determine the MTTF, as well as the upper and lower two-sided 90% confidence limit on this MTTF.
Solution
The following figure shows the data as entered in Weibull++, as well as the calculated parameters.
The following figures show the probability plot with the 90% two-sided confidence bounds and the pdf plot.
Both the reliability and MTTF can be easily obtained from the QCP. The QCP, with results, for both cases is shown in the next two figures.
Example 3
Template loop detected: Template:Example: Normal General Example (RRX Report)
Example 4
Template loop detected: Template:Example: Normal General Example Interval Data
Example 5
Template loop detected: Template:Example: Normal General Example Complete Data
Example 6
Template loop detected: Template:Example: Normal General Example Suspension Data
Example 7
Template loop detected: Template:Example: Normal General Example All Data Type
Example 7
The following examples illustrate the different types of life data that can be analyzed in Weibull++ using the Normal distribution.
Complete Data
Six units are tested to failure. The following hours-to-failure data are obtained: 12125, 11260, 12080, 12825, 13550 and 14670 hours. Assuming that the data are normally distributed, do the following:
- 1. Find the parameters for the data set, using the Rank Regression on X (RRX) parameter estimation method
- 2. Obtain the probability plot for the data with 90%, two-sided Type 1 confidence bounds.
- 3. Obtain the [math]\displaystyle{ pdf }[/math] plot for the data.
- 4. Using the Quick Calculation Pad, determine the reliability for a mission of 11,000 hours, as well as the upper and lower two-sided 90% confidence limit on this reliability.
- 5. 2. Using the Quick Calculation Pad, determine the MTTF, as well as the upper and lower two-sided 90% confidence limit on this MTTF.
Solution
The following figure shows the data as entered in Weibull++, as well as the calculated parameters.
The following figures show the probability plot with the 90% two-sided confidence bounds and the pdf plot.
Both the reliability and MTTF can be easily obtained from the QCP. The QCP, with results, for both cases is shown in the next two figures.
Example 3
Template loop detected: Template:Example: Normal General Example (RRX Report)
Example 4
Template loop detected: Template:Example: Normal General Example Interval Data
Example 5
Template loop detected: Template:Example: Normal General Example Complete Data
Example 6
Template loop detected: Template:Example: Normal General Example Suspension Data
Example 7
Template loop detected: Template:Example: Normal General Example All Data Type