Template:Ald characteristics

Characteristics

• The lognormal distribution is a distribution skewed to the right.

• The [math]\displaystyle{ pdf }[/math] starts at zero, increases to its mode, and decreases thereafter.

Pdf of the lognormal distribution.

The characteristics of the lognormal distribution can be exemplified by examining the two parameters, the log-mean, [math]\displaystyle{ ({{\overline{T}}^{\prime }}), }[/math] and the log-std, [math]\displaystyle{ ({{\sigma }_{{{T}'}}}), }[/math] and the effect they have on the [math]\displaystyle{ pdf }[/math] .
Looking at the Log-Mean [math]\displaystyle{ ({{\overline{T}}^{\prime }}) }[/math]

• The parameter, [math]\displaystyle{ \bar{{T}'} }[/math] , or the log-mean life, or the [math]\displaystyle{ MTT{F}' }[/math] in terms of the logarithm of the [math]\displaystyle{ {T}'s }[/math] is also the scale parameter, and is a unitless number.

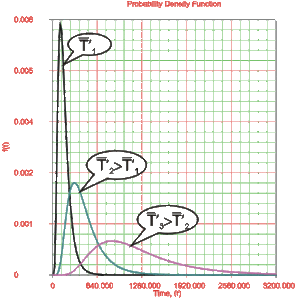
• For the same [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] the [math]\displaystyle{ pdf }[/math] 's skewness increases as [math]\displaystyle{ \bar{{T}'} }[/math] increases.

Pdf of the lognormal distribution with different log-mean values.

Looking at the Log-STD [math]\displaystyle{ ({{\sigma }_{{{T}'}}}) }[/math]

• The parameter [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] , or the standard deviation of the [math]\displaystyle{ {T}'s }[/math] in terms of their logarithm or of their [math]\displaystyle{ {T}' }[/math] , is also the shape parameter, and not the scale parameter as in the normal [math]\displaystyle{ pdf }[/math] . It is a unitless number and assumes only positive values.

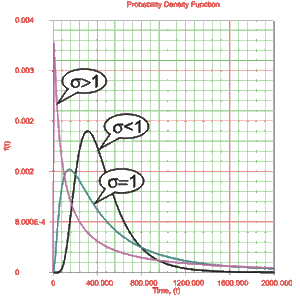
• The degree of skewness increases as [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] increases, for a given [math]\displaystyle{ \bar{{T}'} }[/math] .

• For [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] values significantly greater than 1, the [math]\displaystyle{ pdf }[/math] rises very sharply in the beginning (i.e. for very small values of [math]\displaystyle{ T }[/math] near zero), and essentially follows the ordinate axis, peaks out early, and then decreases sharply like an exponential [math]\displaystyle{ pdf }[/math] or a Weibull [math]\displaystyle{ pdf }[/math] with [math]\displaystyle{ 0\lt \beta \lt 1 }[/math] .

Pdf of the lognormal distribution with different log-std values.