Template:Stress-strength analysis
Stress-Strength Analysis
Stress-Strength analysis has been used in mechanical component design. The probability of failure is based on the probability of stress exceeding strength. The following equation is used to calculate the expected probability of failure:
The expected probability of success or the expected Reliability is calculated as:
The above calculation assumes both stress and strenght have positive domain. For general cases, the expected reliability can be calcualted using the following equation:
where [math]\displaystyle{ L\le {{X}_{1}}\le U }[/math] and:
- [math]\displaystyle{ \begin{align} & {{X}_{1}}:\text{ Stress; } \\ & {{X}_{2}}:\text{ Strength; } \\ \end{align} }[/math]
When U = infinite and L = 0, the above two equations are the same.
Both the stress and strenght distributions can be either estimated from actual data or specified by engineers based on engineering knowledge or existing references. Based on the sources of the distribution, there are two types of variations associated with the calculated probability.
Variation in Model Parameters
If both stress and strength distributions are estimated from data sets, then there are uncertainty associated with the estimated distribution parameters. These uncertainty will cause some degree of variation of the calculated probability from the stress-strength analysis. Therefore, we can use these uncertainty to estimate the confidence interval of the calculated probability. To get the confidence interval, we first calcualte the variance of the Reliablility using:
[math]\displaystyle{ Var\left[ R \right]=\int_{0}^{\infty }{Var\left[ {{f}_{1}}(x) \right]}{{\left[ {{R}_{2}}(x) \right]}^{2}}dx+{{\int_{0}^{\infty }{\left[ {{f}_{1}}(x) \right]}}^{2}}Var\left[ {{R}_{2}}(x) \right]dx }[/math]
Variance of [math]\displaystyle{ {{f}_{1}}(x) }[/math] and [math]\displaystyle{ {{R}_{2}}(x) }[/math] can be estimated from the Fisher Information Matrix. For detail, please see chapter Confidence Bounds.
Once the variance of the expected reliability is obtained, the two-sided confidence interval of it can be calcualted using:
[math]\displaystyle{ [\frac{R}{R+(1-R)w},\frac{R}{R+(1-R)/w}] }[/math]
where CL is the confidence level; [math]\displaystyle{ \alpha }[/math] = 1-CL; [math]\displaystyle{ w=\exp \{{{z}_{1-\alpha /2}}\sqrt{Var(R)}/[R(1-R)]\} }[/math]; [math]\displaystyle{ {{Z}_{1-\alpha /2}} }[/math] is the [math]\displaystyle{ 1-\alpha/2 }[/math] percential of a standard normal distribution.
Variation in Probability Values
Weibull++'s Stress-Strength Wizard allows you to perform such calculations.
The Stress-Strength Calculator is accessible from the Tools folder of the Project Explorer. The tool first asks for the locations of the stress and strength data from among the folios available, as shown below.
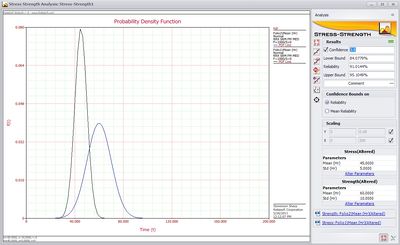
Once the tool knows where to find data for stress and strength, it automatically calculates the reliability and graphs the distributions of the stress and strength data, as shown below.
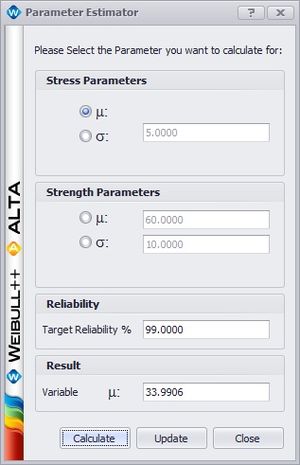
Once the reliability has been calculated, the user has two different options for performing sensitivity analysis (seeing how the system performance changes with changes in parameter values). The user can manually alter the distribution parameters used to calculate the reliability by clicking the “Alter Parameters” link for the appropriate distribution, or the user can use the Parameter Estimator to find what parameters result in a specified target reliability. The “Alter Parameters” link allows the user to manually set what she would like the distribution parameter(s) to be. Alternatively, the Parameter Estimator utility allows the user to select a target reliability to reach and a distribution parameter to adjust. The utility then adjusts the parameter value until the specified target is reached and outputs the parameter value that does so, as shown below.